NiO的DFT+U的电子结构

Nanodcal是一款基于非平衡态格林函数-密度泛函理论（NEGF - DFT）的第一性原理计算软件，主要用于模拟器件材料中的非线性、非平衡的量子输运过程，是目前国内唯一一款拥有自主知识产权的基于第一性原理的输运软件。可预测材料的电流 - 电压特性、电子透射几率等众多输运性质。

迄今为止，Nanodcal 已成功应用于1维、2维、3维材料物性、分子电子器件、自旋电子器件、光电流器件、半导体电子器件设计等重要研究课题中，并将逐步推广到更广阔的电子输运性质研究的领域。

本期将给大家介绍Nanodcal自旋器件1.2的内容。

1.2. NiO 的 DFT+U的电子结构

1.2.1. 研究背景

对于过渡族金属元素主要是3d族，当然也包括4d，5d族，和稀土元素，主要是镧系；这些元素形成的合金或者化合物中，由于存在d电子或f电子，而这两种电子都是强关联电子，在某些时候，传统的DFT没法描述，也就是LDA或GGA计算的结果是不对的，其主要表现在带隙的大小上。产生这种计算错误的结果是LDA或者GGA忽略了d或者f电子的强关联作用，而通过平均场的Hubbard修正，俗称DFT+U（一种半经验修正），可以对使用LDA或者GGA计算的材料的带隙进行修正。本篇工作主要以NiO为例，通过不加U和加U计算NiO的态密度，观察其对带隙的修正作用。

在DFT+U中有一个额外的能量项加入到交换关联能中：

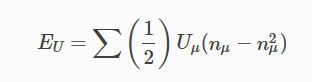
其中，n_μ为原子壳层上的投影，U_μ为原子壳层对应的U值，E_U能量项对于完全占据或未占据的壳层为零，而对于略微占据的壳层为正。

因此，如果状态被完全占据，能量就会降低。这可能发生在能级远离费米能级，即增加能带隙，或如果状态的展宽减小，即电子被局域化。这样，Hubbard U就完善了LDA和GGA的不足之处。

NiO晶体在LDA和GGA中带隙过低，是DFT+U近似可以用来改善固体电子结构描述的标准例子之一。在本教程中，将使用GGA比较该系统的DFT和DFT+U模型。

1.2.2. 计算NiO的态密度

1.2.2.1. 模型搭建

1. 双击图标“Device Studio快捷方式”打开软件；

2. 选择Create a new Project→OK→文件名：NiO，保存类型：ProjectFiles(*.hpf) →保存即可；

3. 右击NiO，选择New→Crystal，输入对应的晶格参数以及原子坐标，并点击Build:

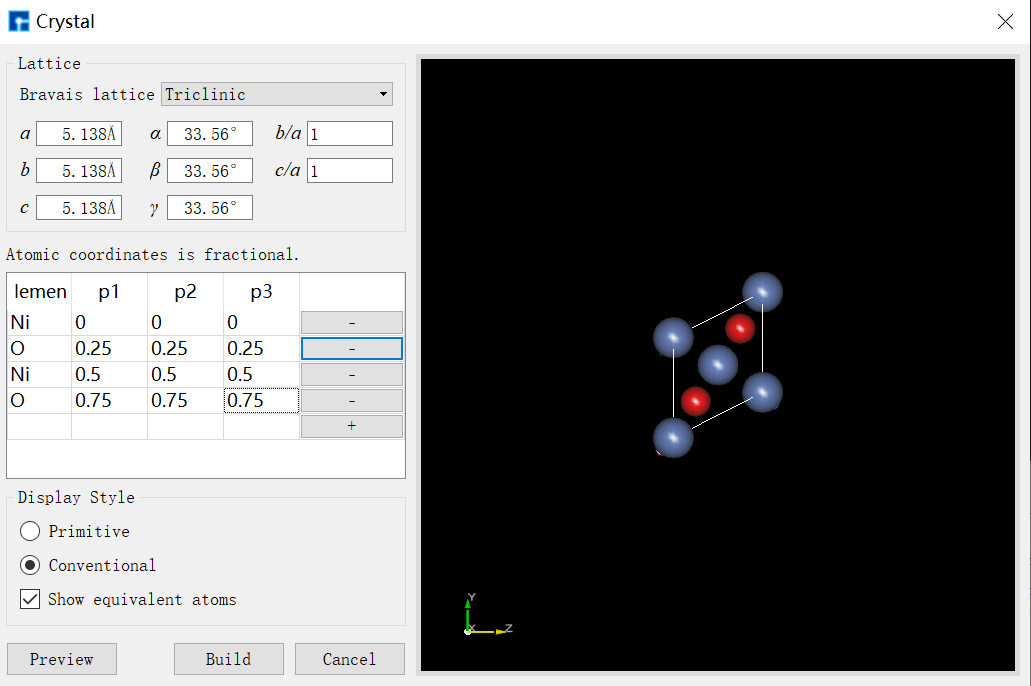
图 1-1：建立晶体NiO结构图

1.2.2.2. 态密度计算（DFT)

1.2.2.2.1. 自洽计算

（1）点击Simulator→Nanodcal→SCF Calculation→Generate file，建立Nanodcal计算所需自洽文件scf.input，Ni_PBE-DZP.nad,O_PBE-DZP.nad

%%What quantities should be calculatedcalculation.name = scf%Basic settingcalculation.occupationFunction.temperature = 300calculation.realspacegrids.E_cutoff = 140 Hartreecalculation.xcFunctional.Type = GGA_PBE96calculation.k_spacegrids.number = [ 6 6 6 ]'system.centralCellVectors = [[5.138 0 0]' [4.28153 2.84034 0]' [4.28153 1.29104 2.52997]']system.spinType = CollinearSpin%Iteration controlcalculation.SCF.monitoredVariableName = {'rhoMatrix','hMatrix','totalEnergy','bandEnergy','gridCharge','orbitalCharge','spinPolar'}calculation.SCF.convergenceCriteria = {1e-04,1e-04,[],[],[],[],[]}calculation.SCF.maximumSteps = 200calculation.SCF.mixMethod = Pulay%Basic setsystem.neutralAtomDataDirectory = '../'system.atomBlock = 4AtomType OrbitalType X Y Z SpinPolarizationNi      PBE-DZP 0.00000000      0.00000000      0.00000000      1O       PBE-DZP 3.42526665      1.03284448      0.63249165      0Ni      PBE-DZP 6.85053331      2.06568896      1.26498329      1O       PBE-DZP 10.27579996     3.09853344      1.89747494      0end

2. 选中scf.input文件右击，点击Run，并选择计算所需的核数：

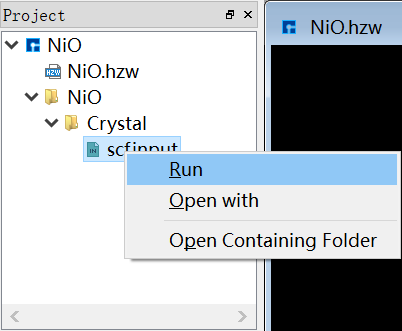
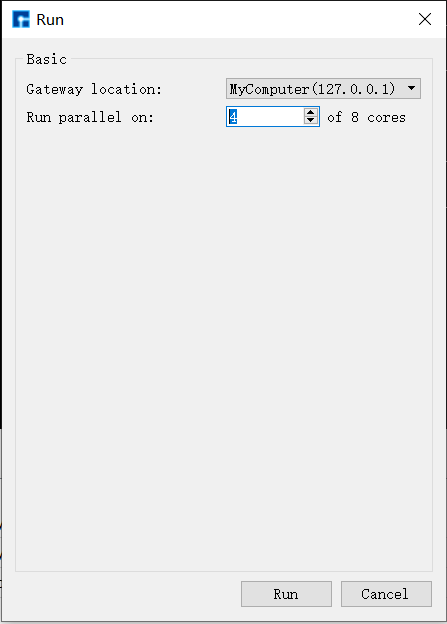
图 1-2：提交自洽计算界面图

3. 在Job manager中出现Finished表示计算结束

图 1-3：NiO自洽计算完成的Device Studio的Job Manager区域

1.2.2.2.2. 态密度计算

1. 在自洽计算的基础上，准备DensityOfStates.input的输入文件，操作如下：

Simulator→Nanodcal→Analysis→DensityOfStates→Generate file

system.object = NanodcalObject.matcalculation.name = densityOfStatescalculation.densityOfStates.kSpaceGridNumber = [ 10 10 10 ]'calculation.densityOfStates.numberOfEnergyPoints = 401calculation.densityOfStates.energyRange = [-10 , 10]calculation.densityOfStates.whatProjected = 'Atom'

2. 计算结束后，可以通过在DS中打开：Simulator→Nanodcal→Analysis Plot，找到对应的DensityOfStates.xml文件，点击打开：

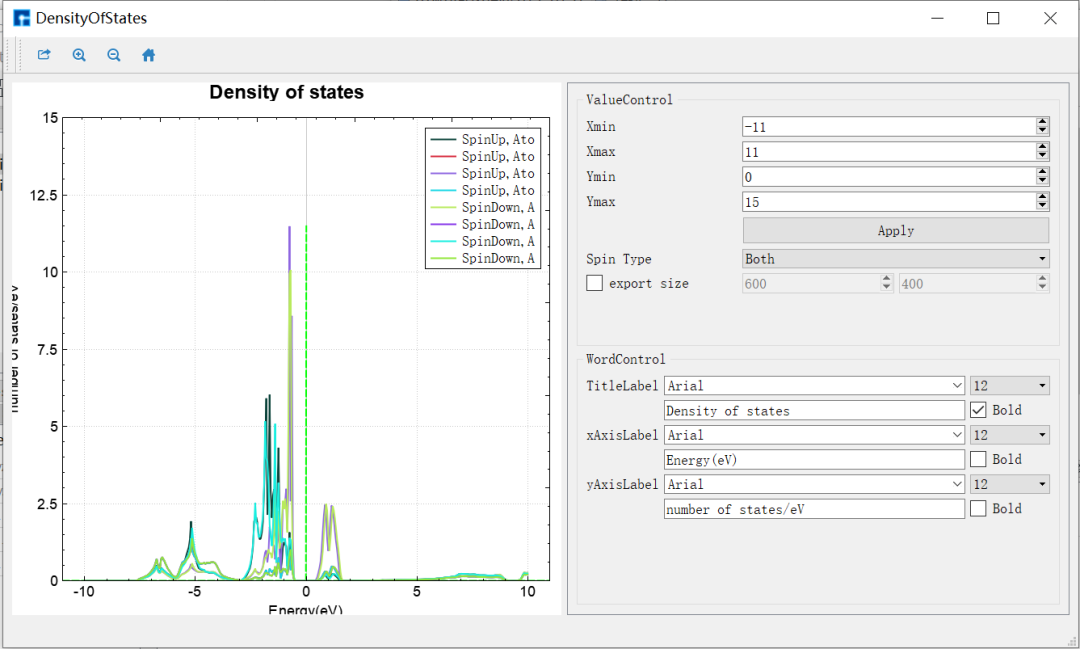
图 1-4：NiO态密度的可视化分析界面

3. 可以通过以下命令将DOS的数据提取出来：

>>data.densityOfStates(:,:,1,:,1)+data.densityOfStates(:,:,3,:,1)

在orgin软件中进行绘制,得到总态密度以及Ni原子的投影态密度，如下图：

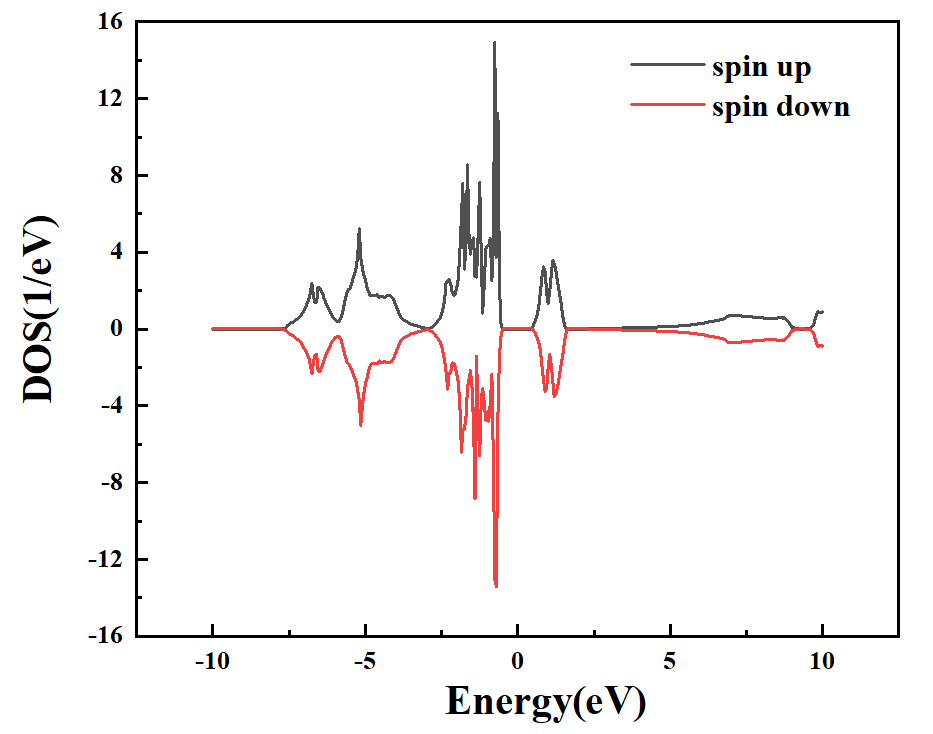
图 1-5：NiO的总态密度图

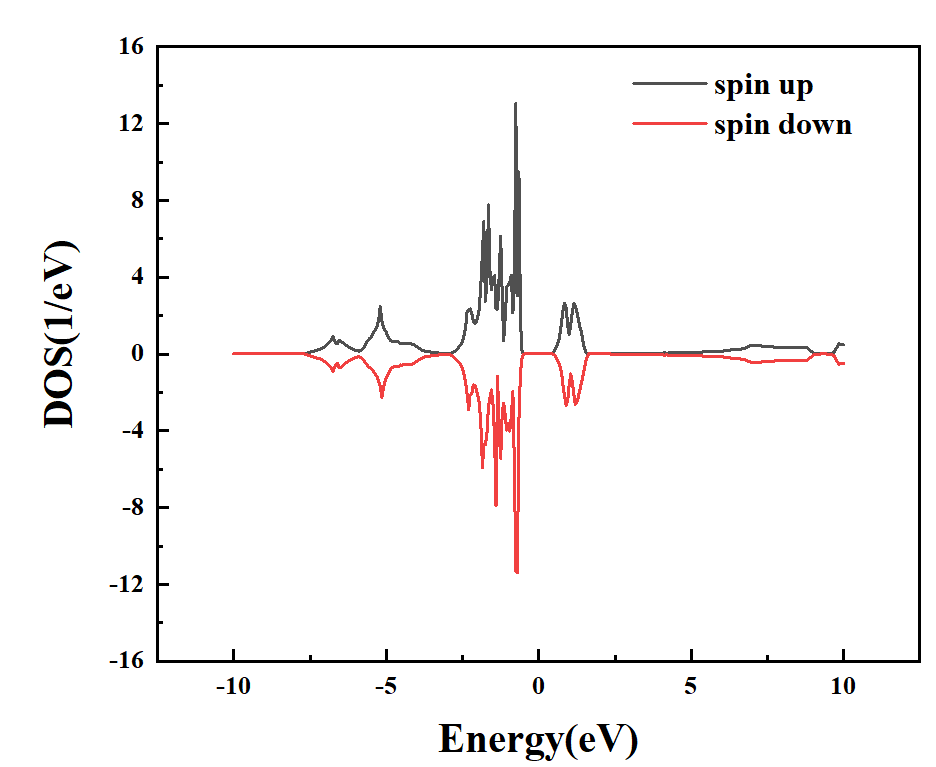
图 1-6：投影到Ni原子的态密度图

1.2.2.3. 态密度计算（DFT+U)

1.2.2.3.1. 自洽计算

（1）点击Simulator→Nanodcal→SCF Calculation→Generate file，建立Nanodcal计算所需自洽文件scf.input,Ni_PBE-DZP.nad,O_PBE-DZP.nad

%%What quantities should be calculatedcalculation.name = scf%Basic settingcalculation.occupationFunction.temperature = 300calculation.realspacegrids.E_cutoff = 140 Hartreecalculation.xcFunctional.Type = GGA_PBE96calculation.k_spacegrids.number = [ 6 6 6 ]'system.centralCellVectors = [[5.138 0 0]' [4.28153 2.84034 0]' [4.28153 1.29104 2.52997]']system.spinType = CollinearSpin%Hubbard U settingcalculation.Hubbard.isIncluded = truecalculation.Hubbard.parameterBlock = 2Ni  PBE-DZP    0.00    0.00    4.60    0.00O  PBE-DZP    0.00    0.00    0.00    0.00end%Iteration controlcalculation.SCF.monitoredVariableName = {'rhoMatrix','hMatrix','totalEnergy','bandEnergy','gridCharge','orbitalCharge','spinPolar'}calculation.SCF.convergenceCriteria = {1e-04,1e-04, [], [], [], [], []}calculation.SCF.maximumSteps = 200calculation.SCF.mixMethod = Pulaycalculation.SCF.mixRate = 0.1calculation.SCF.mixingMode = Hcalculation.SCF.startingMode = H%calculation.SCF.donatorObject = NanodcalObject.mat%Basic setsystem.neutralAtomDataDirectory = '../'system.atomBlock = 4AtomType OrbitalType X Y Z SpinPolarizationNi      PBE-DZP 0.00000000      0.00000000      0.00000000      1O       PBE-DZP 3.42526665      1.03284448      0.63249165      0Ni      PBE-DZP 6.85053331      2.06568896      1.26498329      -1O       PBE-DZP 10.27579996     3.09853344      1.89747494      0end

（2）自洽文件生成后，参照2.2.1中的（2）和（3）进行对应的自洽计算。

1.2.2.3.2. 态密度计算

• （1）在上一步自洽计算的基础上，准备DensityOfStates.input的输入文件，操作如下：

• Simulator→Nanodcal→Analysis→DensityOfStates→Generate file

（2）计算结束后，可以通过在DS中打开:Simulator→Nanodcal→Analysis Plot，找到对应的DensityOfStates.xml文件，点击打开：

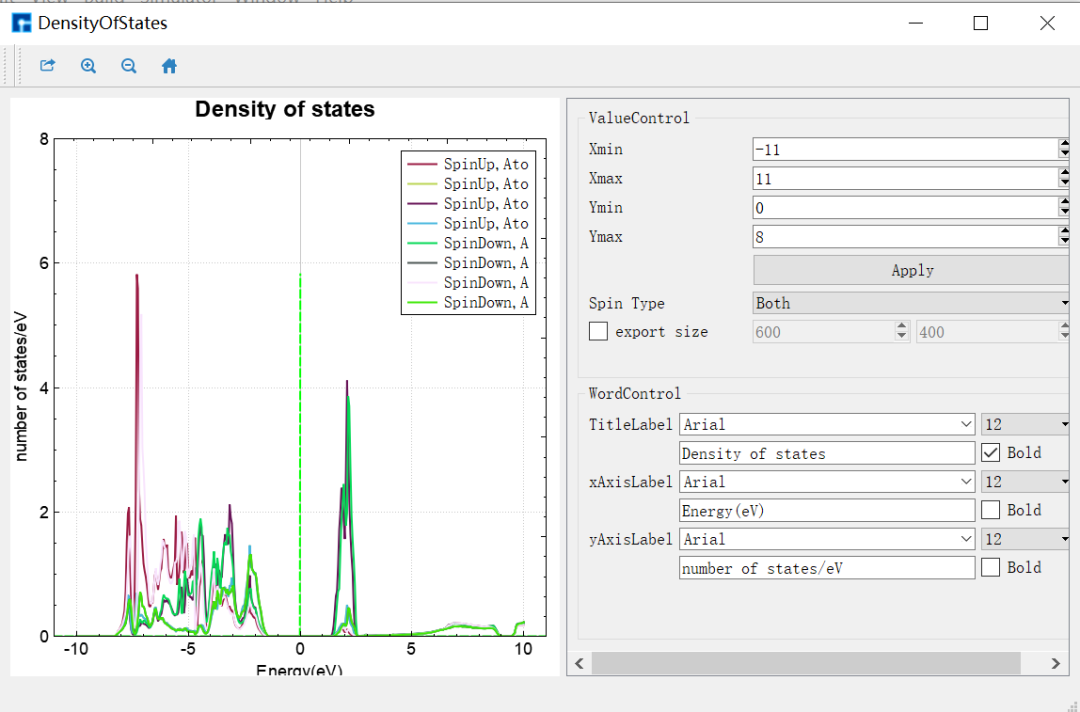
图 1-7：DFT+U的 NiO态密度的可视化分析界面

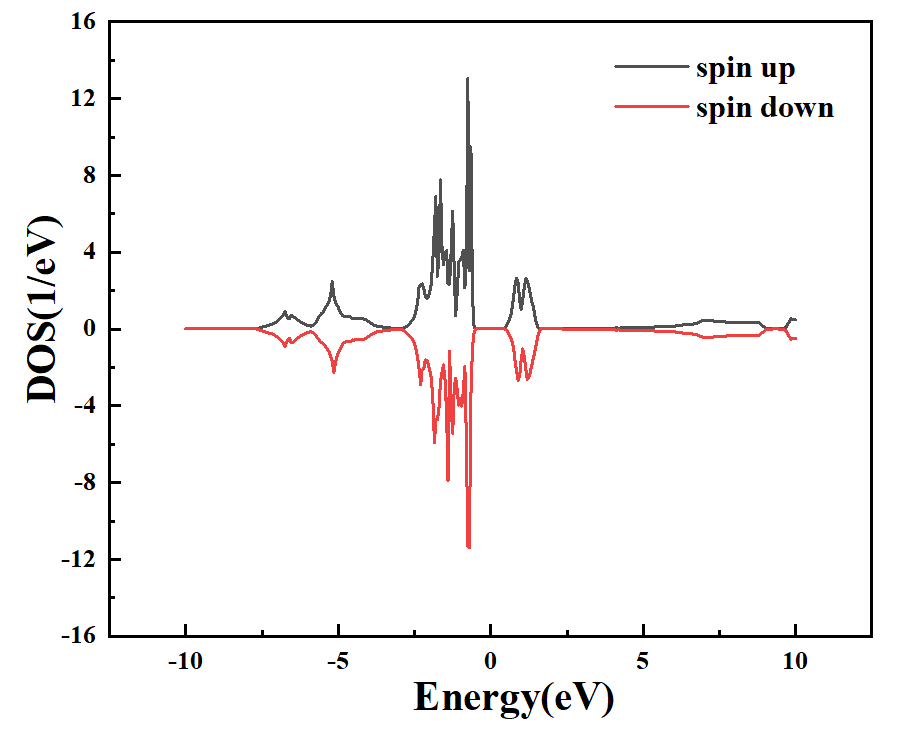
图 1-9：DFT+U的 投影到Ni原子的态密度图

（4)DFT+U相对于DFT的计算，其对带隙的大小有着比较明显的修正作用，所以在计算的过程中根据自己的研究体系，来决定计算是否需要+U，如图：

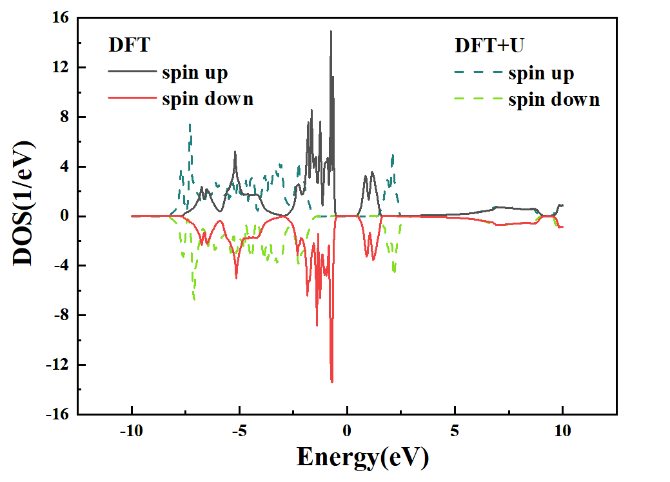
图 1-10

审核编辑 ：李倩