椭偏仪的原理和应用 | 薄膜材料或块体材料光学参数和厚度的测量

椭偏仪是一种基于椭圆偏振分析的光学测量仪器，通过探测偏振光与样品相互作用后偏振态的变化，获取材料的光学常数和结构信息。Flexfilm全光谱椭偏仪可以非接触对薄膜的厚度与折射率的高精度表征，广泛应用于薄膜材料、半导体和表面科学等领域,在材料光学特性分析领域具有重要地位。

1

椭偏仪的基本原理

flexfilm

当偏振光波穿过介质时，会与介质发生相互作用，这种作用会改变光波的偏振态。椭偏仪通过检测偏振态的变化，再经过分析拟合，最终得到所需的材料相关信息。在描述薄膜反射线形成椭圆偏振光的特性时，常用薄膜的椭圆函数 ρ 来表示，表达公式：

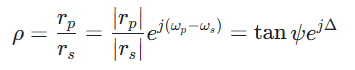
Tanψ:反射光两个偏振分量的振幅系数之比;ψ:偏振角;rp:反射光在 P 平面的偏振分量;rs:反射光在 S 平面的偏振分量

2

关键光学模型及其应用

flexfilm

构建与参数匹配良好的椭偏仪数据处理模型至关重要，若模型错误，测量结果会与真实值偏差极大，误导实验。以下为几种常用的材料物理模型：

NK 模型

适用于已知组分的同类多层膜。

柯西模型

适用于透明材料，如Al₂O₃、SiO₂、MgF₂、SiN4、TiO₂、ITO、KCl 等。在透明波段，采用柯西公式表达材料的光学常数，能获得较高的准确度，其公式为：

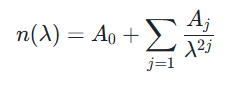
Aj经验参数，λ为波长

柯西指数模型

与柯西模型相比，它的显著特点是吸收系数随频率呈指数变化。它适用于碱卤化物、碱土金属的氟化物、氧化物以及半导体（如可见光和红外波段的Si、GaAs ）等材料。

Sellmeier 模型

非常适用于透明材料（Al₂O₃、SiO₂、MgF₂、SiN4、TiO₂、ITO、KCl 等）和吸收材料（处于红外波段的 Ge、Si、GaAs）。在透明波段的光学常数具有较高的精准度，对于电子跃迁情况，当光波能量远高于带宽时，需同时考虑电子和晶格的贡献，其表达式为：

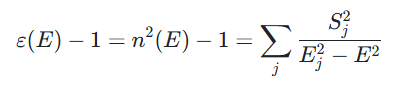
这就是 Sellmeier 公式，在实际应用中用波长代替能量作为参量,公式为：

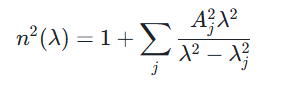
ε(E)：介电函数，(E)：折射率，Sj、Ej、Aj、λj均为相关参数

EMA（有效介质）模型

主要应用于由两种或两种以上不同组份构成的混合介质体系，将混合介质视为一种在特定光谱范围内具有单一有效介电常量张量的“有效介质”，从而建立起均匀薄膜微观结构与宏观介电常数之间的联系。该模型包含以下3 种有效介质类型：

(1)Lorentz-Lorenz 有效介质模型

对于介电函数分别为εa和εb的两种介质随机混合形成的最简单异构介质，其有效介电函数可通过以下公式估算：

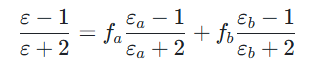
fa、fb分别为两种介质的份额，且满足fa+fb=1

(2)Maxwell-Garnett 有效介质模型

上述 Lorentz-Lorenz 模型假设主介质为真空（即ε=1），而 Maxwell-Garnett 模型考虑了更一般的情况，即主介质的介电函数为εa，次要介质分散于主介质中。

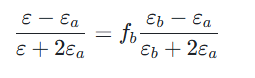
当εh=εa时，有效介质函数ε的表达式

(3)Bruggeman有效介质模型

当不同成分混杂在一起，无法区分主介质时，可采用Bruggeman有效介质模型，fj为第j种介质所占的体积份额，且Σfj=1。在拟合实验数据时，若出现fj<0或fj>1的情况，表明有效介质近似不适用，或者物质的组成模型与实际情况不相符。通常，有效介质模型可用于薄膜粗糙表面和过渡层的分析，其公式为：

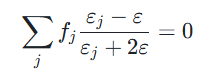
Graded 模型

Graded 模型与 EMA 模型有相似之处，均适用于两种材料的混合材料，但不同的是，Graded 模型中混合材料层内不同深度的混合比是确定的，这一特性使其在特定混合结构薄膜的分析中具有独特优势。

Drude 模型

Drude 模型主要用于金属自由电子气、硅化物以及半导体等材料中的载流子吸收情况，其表达式为：

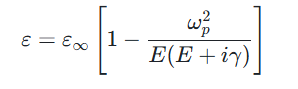
ωp:等离子共振频率，γ:碰撞频率，ε∞:为高频介电常数，E:光子能量

洛仑兹振子模型

洛仑兹认为，物质分子是由一定数量的重原子核和外围电子构成的复杂带电系统，固体的介电函数可通过一定数量的洛仑兹振子的和近似表示，这一近似被称为简谐振子近似，简谐振子模型适用于晶态半导体材料，当材料特征不明确时，选用该模型进行分析是较为合适的选择,其表达式为：

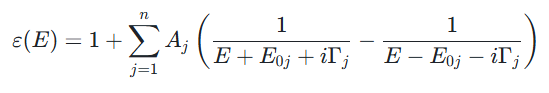
Aj:振幅,与载流子密度、电荷、质量相关；E0j:振子的共振能量；Γj:振子的展宽系数,与振子的阻力有关

Forouhi-Bloomer 模型

Forouhi 和 Bl oomer 针对非晶态半导体，通过量子力学处理并结合Kramers-Kronig关系，推导出包含 5 个参数的 Forouhi-Bloomer 模型，该模型更适合分析铁电薄膜与半导体薄膜材料，其相关公式如下：

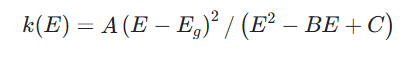
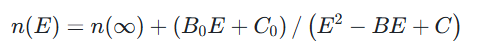
n(∞):无穷大能量时的折射率，Eg、A、B、C均为正的常数，κ(E):吸收系数，n(E):折射率

形模型

为了在较宽的频谱范围内准确表达物质的光学常数，通常需要综合考虑上述多种模型，由此形成了形模型，其表达式为：

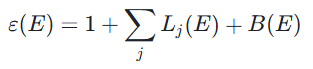
L(E):某些特定的线形，如高斯线形、洛伦兹形、临界点线形等，B(E):能量缓变的背景

3

数据处理程序

flexfilm

主要包含以下步骤：设计参数→在设计窗口输入材料→最优化窗口导入数据→材料窗口挑选物理模型→对透射系数、吸收系数、反射系数以及椭偏参数Δ、Ψ等进行计算→设定最大和最小厚度

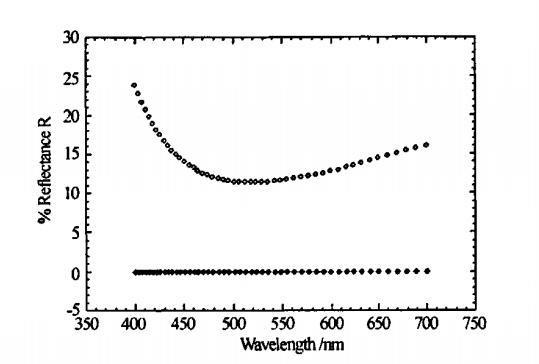
Si衬底上某种薄膜反射率的最优化图像

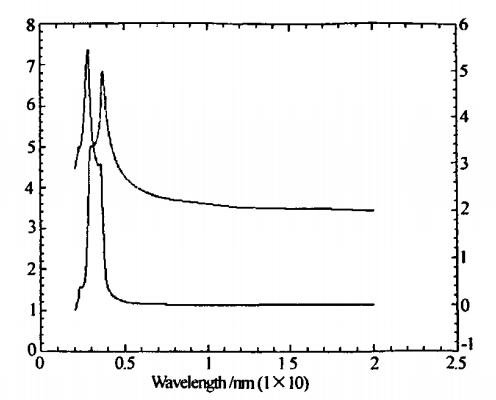
Si衬底的n、k图

椭偏仪测量薄膜具有广泛适用性，尺寸要求极低，方式灵活，较快的测量速度，表面造成的损伤最小，从偏振态变化提取结构信息，介电函数分析电子与几何结构等优点。椭偏光谱技术可以应用在固体薄膜光学性质测量、物理吸附与化学吸附、界面与表面分析、电化学、微电子等领域。

Flexfilm全光谱椭偏仪

flexfilm

全光谱椭偏仪拥有高灵敏度探测单元和光谱椭偏仪分析软件，专门用于测量和分析光伏领域中单层或多层纳米薄膜的层构参数（如厚度）和物理参数（如折射率n、消光系数k）

• 先进的旋转补偿器测量技术：无测量死角问题。
• 粗糙绒面纳米薄膜的高灵敏测量：先进的光能量增强技术，高信噪比的探测技术。
• 秒级的全光谱测量速度：全光谱测量典型5-10秒。
• 原子层量级的检测灵敏度：测量精度可达0.05nm。

Flexfilm全光谱椭偏仪能非破坏、非接触地原位精确测量超薄图案化薄膜的厚度、折射率,结合费曼仪器全流程薄膜测量技术，助力半导体薄膜材料领域的高质量发展。

原文参考：《椭偏仪的原理和应用》

*特别声明：本公众号所发布的原创及转载文章，仅用于学术分享和传递行业相关信息。未经授权，不得抄袭、篡改、引用、转载等侵犯本公众号相关权益的行为。内容仅供参考，如涉及版权问题，敬请联系，我们将在第一时间核实并处理。