图扑 HT 总线式拓扑图的可视化实现

在图形用户界面（GUI）设计中，自定义连线技术不仅提升了用户体验，还为复杂数据可视化开辟了新的可能性。该功能点允许用户灵活地在界面元素之间创建视觉连接，使流程图、思维导图和网络拓扑图等信息呈现更加直观和动态。

图扑软件自研 HT for Web 产品框架中，ht.Edge 节点用于表示节点间的连线关系。熟悉 HT 的用户应该了解 ht.Edge 内置了多种连线类型，能满足一般拓扑图需求，但在特殊情况下，这些默认类型可能无法满足需求。为此，HT 提供了自定义连线功能，允许开发者根据具体需求创建特殊的连线类型，实现更灵活的图形表示。

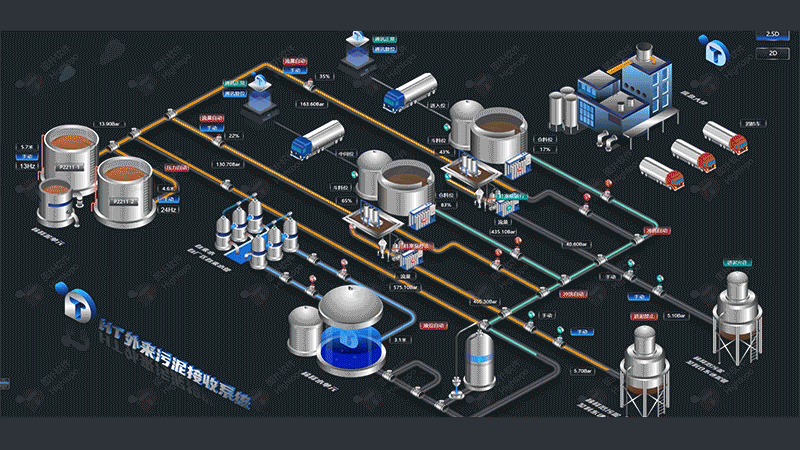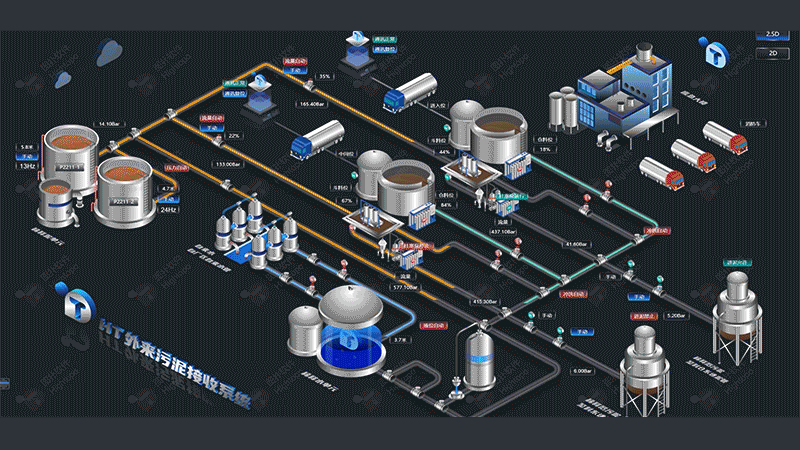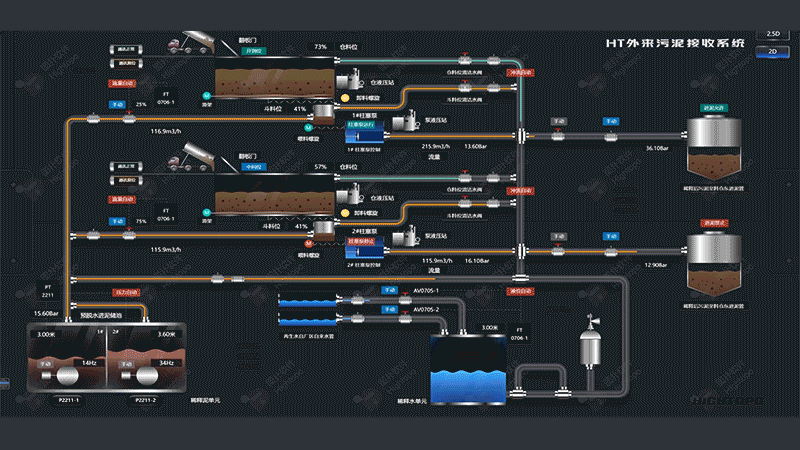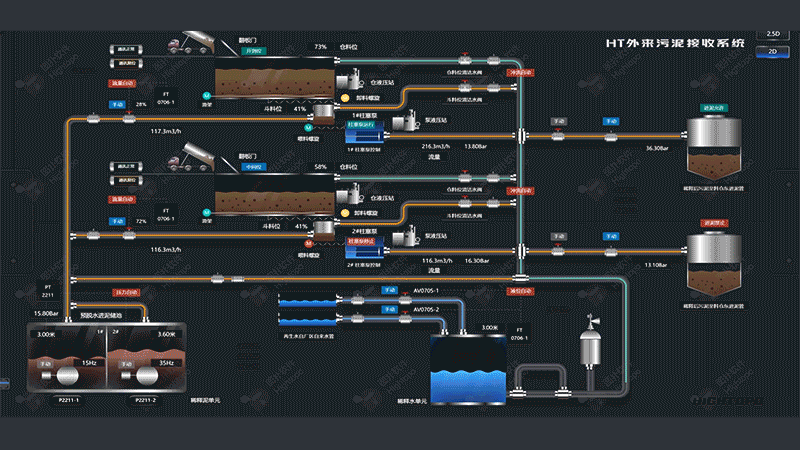
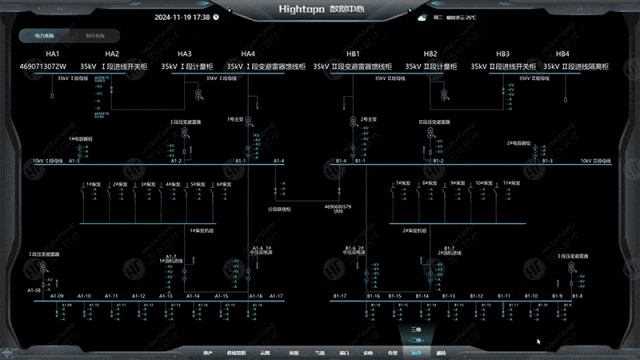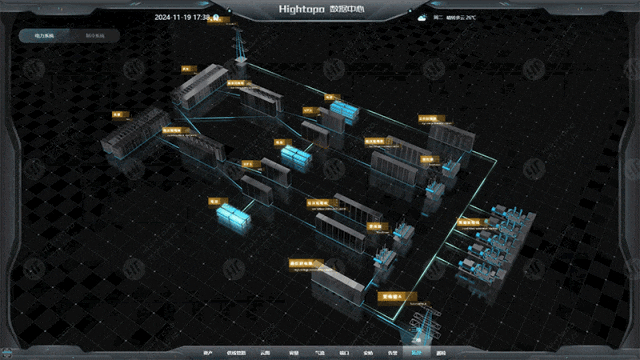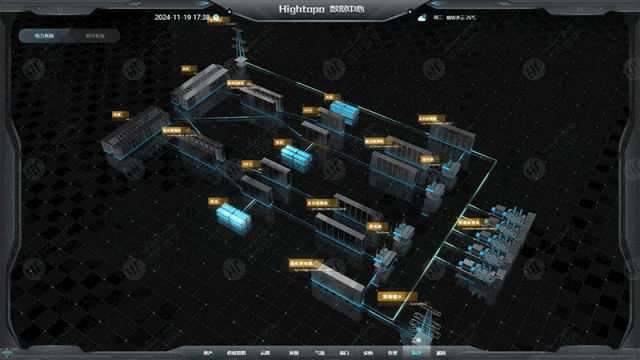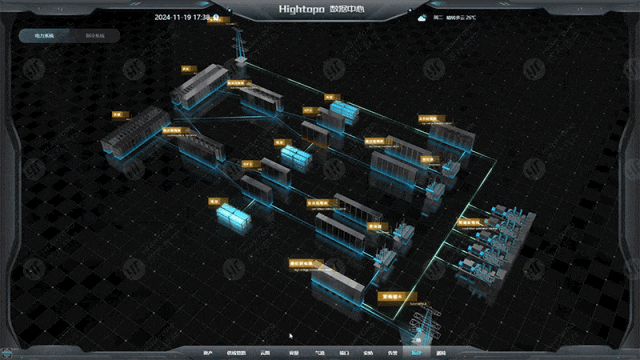
自定义连线

图扑 HT 框架提供灵活的自定义连线功能，开发者可以通过调用 ht.Default.setEdgeType(type, func, mutual) 方法来创建独特的连线类型。以下是该方法的参数详解：

■type：自定义连线类型的名称，与 style 中的 edge.type 属性相对应。

■func：计算连线路径信息的函数，接收四个参数：

gap：多条连线成捆时，本连线对象对应中心连线的间距。

edge：当前连线对象。

graphView：当前对应拓扑组件对象。

sameSourceWithFirstEdge：boolean 类型，该连线是否与同组的第一条连线同源。

■mutual：决定该连线类型是否会影响同一起始或结束节点上的其他连线。

接下来，我们深入分析一种常见的拓扑关系实现步骤，即"横-竖-横"的连线方式。

下面是一段定义上图连线类型的示例代码。代码很简单，首先获取起始节点和目标节点的信息，然后根据这两个节点的坐标，按照预定的规则计算出连线的路径点。

ht.Default.setEdgeType('horizontal-vertical', function (edge, gap, graphView) {

const points = new ht.List();

const segments = new ht.List();

const source = edge.getSource();

const target = edge.getTarget();

const sourceP = source.p();

const targetP = target.p();

points.add(sourceP);

if (targetP.x !== sourceP.x) {

points.add({ x: sourceP.x + (targetP.x - sourceP.x) / 2, y: sourceP.y });

points.add({ x: sourceP.x + (targetP.x - sourceP.x) / 2, y: targetP.y });

}

points.add(targetP);

return { points, segments };

})

定义好连线类型后，只需通过 edge.s('edge.type', 'horizontal-vertical') 这段简单的代码行，就能将 edge 对象的连线设置为我们刚刚定义的类型。由此一来，即可看到令人满意的效果，大幅提升图形的可读性和美观度。

总线拓扑

总线拓扑是一种网络结构，所有设备（如计算机、打印机等）都连接到一个共同的通信介质上，通常是一根电缆，这个介质被称为"总线"（bus）。总线拓扑在工业控制和嵌入式系统等特定领域中被广泛应用。在图扑 HT 框架中，我们可以利用 ht.Shape 组件绘制总线，并通过 ht.Edge 组件将各个设备节点连接到总线上。这些连接的视觉表现可通过自定义连线类型灵活定义，从而实现精确的总线拓扑图表示。

上面展示的是一个总线的示例效果，可以直观看到所有设备都连接到了总线上。在具体实现过程中，最具挑战性的问题是：如何计算出总线上距离目标节点坐标最近的点?

计算节点到总线距离

总线通常由多条直线段组成，因此计算某一节点到总线的最短距离可按以下思路进行：

将总线分割为多段直线

总线由多个直线段构成，可以取总线上相邻两点构成一条直线。具体实现时，遍历 points 数据，获取 points[index] 和 points[index+1] 作为线段的两个端点。注意，如果设置了 segments，其中 1 代表新路径的起点，所以当 segments[index+1] 为 1 时应跳过。

计算点到每条直线的距离

获取每条直线段后，计算节点坐标到各线段的距离，并将距离值存入一个集合中。

获取最短距离

从距离集合中找出最小值，即为节点到总线的最短距离。

基于上述思路，我们可以实现一个总线连线类型。以下是具体的实现代码：

// 计算点到直线的距离，返回结果是个对象结构

var pointToInsideLine = function (p1, p2, p) {

var x1 = p1.x,

y1 = p1.y,

x2 = p2.x,

y2 = p2.y,

x = p.x,

y = p.y,

result = {},

dx = x2 - x1,

dy = y2 - y1,

d = Math.sqrt(dx * dx + dy * dy),

ca = dx / d, // cosine

sa = dy / d, // sine

mX = (-x1 + x) * ca + (-y1 + y) * sa;

result.x = x1 + mX * ca;

result.y = y1 + mX * sa;

if (!isPointInLine(result, p1, p2)) {

result.x = Math.abs(result.x - p1.x) < Math.abs(result.x - p2.x) ? p1.x : p2.x;

result.y = Math.abs(result.y - p1.y) < Math.abs(result.y - p2.y) ? p1.y : p2.y;

}

dx = x - result.x;

dy = y - result.y;

result.z = Math.sqrt(dx * dx + dy * dy);

return result;

};

// 判断点是否在线上

var isPointInLine = function (p, p1, p2) {

return p.x >= Math.min(p1.x, p2.x) &&

p.x <= Math.max(p1.x, p2.x) &&

p.y >= Math.min(p1.y, p2.y) &&

p.y <= Math.max(p1.y, p2.y);

};

// 注册连线类型

ht.Default.setEdgeType('bus', function (edge) {

var source = edge.getSourceAgent(),

target = edge.getTargetAgent();

var targetP = target.p();

var points = source.getPoints().toArray();

var segments = source.getSegments();

var beginPoint;

for (let i = 0; i < points.length - 1; i++) {

if (segments) {

if (segments[i + 1] === 1) continue;

}

const point1 = points[i];

const point2 = points[i + 1];

const minPosition = pointToInsideLine(point1, point2, targetP);

if (!beginPoint || minPosition.z < beginPoint.z) {

beginPoint = minPosition;

}

}

return {

points: new ht.List([ beginPoint, targetP ]),

segments: new ht.List([1, 2])

};

});

执行上述代码后，我们将得到如下效果：

从上图可以清楚看出，示例成功获取了节点到总线的最近点，并绘制了相应的连线节点。值得注意的是，对于直线段而言，节点在直线上的投影点即为其距总线最近的点。

视觉美感优化

虽然示例已实现了基础总线效果，但由于拓扑图采用 2.5D 效果，仅计算投影点可能无法呈现理想的视觉效果。为了增强视觉表现，我们可以考虑让连线旋转一定角度。为此，我们可以在现有功能的基础上添加旋转代码，使连线与整体图形更加协调，提升视觉美感。

ht.Default.setEdgeType('bus', function (edge) {

var source = edge.getSourceAgent(),

target = edge.getTargetAgent();

var targetP = target.p();

var points = source.getPoints().toArray();

var segments = source.getSegments();

var beginPoint, linePoints;

for (let i = 0; i < points.length - 1; i++) {

if (segments) {

if (segments[i + 1] === 1) continue;

}

const point1 = points[i];

const point2 = points[i + 1];

const minPosition = pointToInsideLine(point1, point2, targetP);

if (!beginPoint || minPosition.z < beginPoint.z) {

beginPoint = minPosition;

linePoints = [point1, point2]

}

}

var rotation = angleBetweenLineAndHorizontal(linePoints[0], linePoints[1]);

var rotatePoint = findIntersection([rotatePointAroundAnotherPoint(beginPoint, targetP, rotation), targetP], linePoints);

if(isPointInLine(rotatePoint, linePoints[0], linePoints[1])){

beginPoint = rotatePoint;

}

return {

points: new ht.List([

beginPoint, targetP

]),

segments: new ht.List([1, 2])

};

});

/**

* 计算两点之间直线与水平线的夹角

*/

function angleBetweenLineAndHorizontal(p1, p2) {

if (new ht.Math.Vector2(p1.x, p1.y).length() > new ht.Math.Vector2(p2.x, p2.y).length()) {

var p = p2;

p2 = p1;

p1 = p;

}

var x1 = p1.x,

y1 = p1.y,

x2 = p2.x,

y2 = p2.y;

var dx = x2 - x1;

var dy = y2 - y1;

var angleRadians = Math.atan2(dy, dx); // 计算夹角（弧度）

var angleDegrees = angleRadians * (180 / Math.PI); // 弧度转角

// 确保角度在 0 到 360 之间

if (angleDegrees < 0) {

angleDegrees += 360;

}

return angleDegrees;

}

function rotatePointAroundAnotherPoint(point, center, angleDegrees) {

var angleRadians = angleDegrees * (Math.PI / 180);

var cosTheta = Math.cos(angleRadians);

var sinTheta = Math.sin(angleRadians);

var translatedX = point.x - center.x;

var translatedY = point.y - center.y;

var rotatedX = translatedX * cosTheta - translatedY * sinTheta;

var rotatedY = translatedX * sinTheta + translatedY * cosTheta;

var finalX = rotatedX + center.x;

var finalY = rotatedY + center.y;

return { x: finalX, y: finalY };

}

/**

* 给定两个点，计算直线的系数 A, B, C

* 直线方程：Ax + By = C

*/

function getLineEquation(x1, y1, x2, y2) {

var A = y2 - y1;

var B = x1 - x2;

var C = A * x1 + B * y1;

return { A, B, C };

}

/**

* 计算两条直线的交点

*/

function calculateIntersection(line1, line2) {

var { A: A1, B: B1, C: C1 } = line1;

var { A: A2, B: B2, C: C2 } = line2;

var determinant = A1 * B2 - A2 * B1;

if (determinant === 0) {

// 平行或重合

return null;

} else {

var x = (C1 * B2 - C2 * B1) / determinant;

var y = (A1 * C2 - A2 * C1) / determinant;

return { x, y };

}

}

/**

* 找到两条线的交点，或者延长线的交点

*/

function findIntersection(line1Points, line2Points) {

var [p1, p2] = line1Points;

var [p3, p4] = line2Points;

var line1 = getLineEquation(p1.x, p1.y, p2.x, p2.y);

var line2 = getLineEquation(p3.x, p3.y, p4.x, p4.y);

var intersection = calculateIntersection(line1, line2);

return intersection;

}

实现的最终效果如下：

图扑软件 HT 自定义连线功能为图形交互设计开辟了广阔的新天地。从基本的"横-竖-横"连线到复杂的总线拓扑图，不仅提升了数据可视化的灵活性，还大幅增强了用户体验。通过精细调整连线的旋转角度和投影点，在 2.5D 效果中呈现更加美观和直观的拓扑关系。

不仅适用于网络结构的展示，还可扩展到各种复杂系统的可视化中。为设计师和开发者提供了强大的工具，帮助他们创造出更加丰富、富有表现力的图形界面。

审核编辑 黄宇