概论
上一篇文章 我们分析了矩阵类动态规划,说到这类动态规划通常在一个矩阵中进行,我们只需要考虑当前位置的信息即可,分析并定义状态的时候,也只需要分析当前位置和其相邻位置的关系,通常这样做就可以达到拆解问题的目的。
这次再来看一类动态规划问题,序列类动态规划问题,这类动态规划问题较为普遍,分析难度相比之前也略有提升,通常问题的输入参数会涉及数组或是字符串。
在开始之前,先解释一下子数组(子串)和子序列的区别,你可以看看下面这个例子:
输入数组:[1,2,3,4,5,6,7,8,9] 子数组:[2,3,4],[5,6,7],[6,7,8,9],... 子序列:[1,5,9],[2,3,6],[1,8,9],[7,8,9],...
可以看到的是,子数组必须是数组中的一个连续的区间,而子序列并没有这样一个要求。
你只需要保证子序列中的元素的顺序和原数组中元素的顺序一致即可,例如,在原数组中,元素 1 出现在元素 9 之前,那么在子序列中,如果这两个元素同时出现,那么 1 也必须在 9 之前。
为什么要说这个?
不知道你有没有发现,这里的子数组的问题和我们前面提到的矩阵类动态规划的分析思路很类似,只需要考虑当前位置,以及当前位置和相邻位置的关系。
通过这样的分析就可以把之前讲的内容和今天要介绍的内容关联起来了,相比矩阵类动态规划,序列类动态规划最大的不同在于,对于第 i 个位置的状态分析,它不仅仅需要考虑当前位置的状态,还需要考虑前面 i - 1 个位置的状态,这样的分析思路其实可以从子序列的性质中得出。
对于这类问题的问题拆解,有时并不是那么好发现问题与子问题之间的联系,但是通常来说思考的方向其实在于寻找当前状态和之前所有状态的关系,我们通过几个非常经典的动态规划问题来一起看看。
题目分析
最长上升子序列
LeetCode 第 300 号问题:最长上升子序列。
题目描述
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入:[10,9,2,5,3,7,101,18] 输出:4 解释:最长的上升子序列是[2,3,7,101],它的长度是 4。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶:你能将算法的时间复杂度降低到 O(n log n) 吗?
题目解析
给定一个数组,求最长递增子序列。因为是子序列,这样对于每个位置的元素其实都存在两种可能,就是选和不选,如果我们用暴力的解法,枚举出所有的子序列,然后判断他们是不是递增的,选取最大的递增序列,这样做的话,时间复杂度是 O(2^n),显然不高效。
那这里我们就需要思考用动态规划进行优化,我们按之前的四个步骤来具体分析一下:
问题拆解
我们要求解的问题是 “数组中最长递增子序列”,一个子序列虽然不是连续的区间,但是它依然有起点和终点,比如:
[10,9,2,5,3,7,101,18] 子序列[2,3,7,18]的起始位置是2,终止位置是18 子序列[5,7,101]的起始位置是5,终止位置是101
如果我们确定终点位置,然后去看前面 i - 1 个位置中,哪一个位置可以和当前位置拼接在一起,这样就可以把第 i 个问题拆解成思考之前 i - 1 个问题,注意这里我们并不是不考虑起始位置,在遍历的过程中我们其实已经考虑过了。
状态定义
问题拆解中我们提到 “第 i 个问题和前 i - 1 个问题有关”,也就是说 “如果我们要求解第 i 个问题的解,那么我们必须考虑前 i - 1 个问题的解”,我们定义dp[i] 表示以位置 i 结尾的子序列的最大长度,也就是说 dp[i] 里面记录的答案保证了该答案表示的子序列以位置 i 结尾。
递推方程
对于 i 这个位置,我们需要考虑前 i - 1 个位置,看看哪些位置可以拼在 i 位置之前,如果有多个位置可以拼在 i 之前,那么必须选最长的那个,这样一分析,递推方程就有了:
dp[i]=Math.max(dp[j],...,dp[k])+1, 其中inputArray[j]< inputArray[i], inputArray[k] < inputArray[i]
实现
在实现这里,我们需要考虑状态数组的初始化,因为对于每个位置,它本身其实就是一个序列,因此所有位置的状态都可以初始化为 1。
最后提一下,对于这道题来说,这种方法其实不是最优的,但是在这里的话就不展开讲了,理解序列类动态规划的解题思路是关键。
参考代码
//@五分钟学算法 //www.cxyxiaowu.com publicintlengthOfLIS(int[]nums){ if(nums==null||nums.length==0){ return0; } //dp[i]->thelongestlengthsequencefrom0-i,andmustincludenums[i] int[]dp=newint[nums.length]; Arrays.fill(dp,1); intmax=0; for(inti=0;i< nums.length; ++i) { for (int j = 0; j < i; ++j) { if (nums[i] >nums[j]){ dp[i]=Math.max(dp[j]+1,dp[i]); } } max=Math.max(max,dp[i]); } returnmax; }粉刷房子
LeetCode 第 256 号问题:粉刷房子。
注意:本题为 LeetCode 的付费题目,需要开通会员才能解锁查看与提交代码。
题目描述
假如有一排房子,共 n 个,每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种,你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。
当然,因为市场上不同颜色油漆的价格不同,所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的矩阵来表示的。
例如,costs[0][0]表示第 0 号房子粉刷成红色的成本花费;costs[1][2]表示第 1 号房子粉刷成绿色的花费,以此类推。请你计算出粉刷完所有房子最少的花费成本。
注意:
所有花费均为正整数。
示例:
输入:[[17,2,17],[16,16,5],[14,3,19]] 输出:10 解释:将0号房子粉刷成蓝色,1号房子粉刷成绿色,2号房子粉刷成蓝色。 最少花费:2+5+3=10。
题目解析
给 n 个房子刷油漆,有三种颜色的油漆可以刷,必须保证相邻房子的颜色不能相同,输入是一个 n x 3 的数组,表示每个房子使用每种油漆所需要花费的价钱,求刷完所有房子的最小价值。
还是按原来的思考方式走一遍:
问题拆解
对于每个房子来说,都可以使用三种油漆当中的一种,如果说不需要保证相邻的房子的颜色必须不同,那么整个题目会变得非常简单,每个房子直接用最便宜的油漆刷就好了,但是加上这个限制条件,你会发现刷第 i 个房子的花费其实是和前面 i - 1 个房子的花费以及选择相关,如果说我们需要知道第 i 个房子使用第 k 种油漆的最小花费,那么你其实可以思考第 i - 1 个房子如果不用该油漆的最小花费,这个最小花费是考虑从 0 到当前位置所有的房子的。
状态定义
通过之前的问题拆解步骤,状态可以定义成 dp[i][k],表示如果第 i 个房子选择第 k 个颜色,那么从 0 到 i 个房子的最小花费
递推方程
基于之前的状态定义,以及相邻的房子不能使用相同的油漆,那么递推方程可以表示成:
dp[i][k]=Math.min(dp[i-1][l],...,dp[i-1][r])+costs[i][k],l!=k,r!=k
实现
因为我们要考虑 i - 1 的情况,但是第 0 个房子并不存在 i - 1 的情况,因此我们可以把第 0 个房子的最小花费存在状态数组中,当然你也可以多开一格 dp 状态,其实都是一样的。
对于这道题目,你可能会问这不是和矩阵类动态规划类似吗?
如果单从房子来考虑的确是,但是对于颜色的话,我们必须考虑考虑相邻房子的所有颜色,这就有点序列的意思在里面了。
另外对于题目的分类其实没有严格的限定,主要是为了把相类似的问题放在一起,这样有便于分析问题思路。
参考代码
//@五分钟学算法 //www.cxyxiaowu.com publicintminCost(int[][]costs){ if(costs==null||costs.length==0){ return0; } intn=costs.length; int[][]dp=newint[n][3]; for(inti=0;i< costs[0].length; ++i) { dp[0][i] = costs[0][i]; } for (int i = 1; i < n; ++i) { dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2]) + costs[i][0]; dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2]) + costs[i][1]; dp[i][2] = Math.min(dp[i - 1][0], dp[i - 1][1]) + costs[i][2]; } return Math.min(dp[n - 1][0], Math.min(dp[n - 1][1], dp[n - 1][2])); }粉刷房子II
LeetCode 第 265 号问题:粉刷房子II。
注意:本题为 LeetCode 的付费题目,需要开通会员才能解锁查看与提交代码。
题目描述
假如有一排房子,共 n 个,每个房子可以被粉刷成 k 种颜色中的一种,你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。
当然,因为市场上不同颜色油漆的价格不同,所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x k 的矩阵来表示的。
例如,costs[0][0] 表示第 0 号房子粉刷成 0 号颜色的成本花费;costs[1][2] 表示第 1 号房子粉刷成 2 号颜色的成本花费,以此类推。请你计算出粉刷完所有房子最少的花费成本。
注意:
所有花费均为正整数。
示例:
输入:[[1,5,3],[2,9,4]] 输出:5 解释:将0号房子粉刷成0号颜色,1号房子粉刷成2号颜色。最少花费:1+4=5; 或者将0号房子粉刷成2号颜色,1号房子粉刷成0号颜色。最少花费:3+2=5.
进阶:
您能否在 O(nk) 的时间复杂度下解决此问题?
题目解析
上面那道题目的 follow up,现在不是三种油漆,而是 k 种油漆。
其实解题思路还是不变。
对于第 i 个房子的每种颜色,我们对比看第 i - 1 个房子的 k 种油漆,找到不相重的最小值就好,但是这里的时间复杂度是 O(n*k^2)。
其实这是可以优化的,我们只需要在第 i - 1 个位置的状态中找到最大值和次大值,在选择第 i 个房子的颜色的时候,我们看当前颜色是不是和最大值的颜色相重,不是的话直接加上最大值,如果相重的话,我们就加上次大值,这样一来,我们把两个嵌套的循环,拆开成两个平行的循环,时间复杂度降至 O(n*k)。
参考代码(优化前)
//@五分钟学算法 //www.cxyxiaowu.com publicintminCostII(int[][]costs){ if(costs.length==0||costs[0].length==0){ return0; } intn=costs.length,k=costs[0].length; int[][]dp=newint[n][k]; for(inti=1;i< n; ++i) { Arrays.fill(dp[i], Integer.MAX_VALUE); } for (int i = 0; i < k; ++i) { dp[0][i] = costs[0][i]; } for (int i = 1; i < n; ++i) { for (int j = 0; j < k; ++j) { for (int m = 0; m < k; ++m) { if (m != j) { dp[i][m] = Math.min(dp[i][m], dp[i - 1][j] + costs[i][m]); } } } } int result = Integer.MAX_VALUE; for (int i = 0; i < k; ++i) { result = Math.min(result, dp[n - 1][i]); } return result; }
参考代码(优化后)
//@五分钟学算法 //www.cxyxiaowu.com publicintminCostII(int[][]costs){ if(costs.length==0||costs[0].length==0){ return0; } intn=costs.length,k=costs[0].length; int[][]dp=newint[n][k]; for(inti=1;i< n; ++i) { Arrays.fill(dp[i], Integer.MAX_VALUE); } for (int i = 0; i < k; ++i) { dp[0][i] = costs[0][i]; } for (int i = 1; i < n; ++i) { // min1 表示的是最大值,min2 表示的是次大值 int min1 = Integer.MAX_VALUE, min2 = Integer.MAX_VALUE; int minIndex = -1; for (int l = 0; l < k; ++l) { if (min1 >dp[i-1][l]){ min2=min1; min1=dp[i-1][l]; minIndex=l; }elseif(min2>dp[i-1][l]){ min2=dp[i-1][l]; } } for(intj=0;j< k; ++j) { if (minIndex != j) { dp[i][j] = Math.min(dp[i][j], min1 + costs[i][j]); } else { dp[i][j] = Math.min(dp[i][j], min2 + costs[i][j]); } } } int result = Integer.MAX_VALUE; for (int i = 0; i < k; ++i) { result = Math.min(result, dp[n - 1][i]); } return result; }打家劫舍
LeetCode 第 198 号问题:打家劫舍。
题目描述
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋(金额= 1),然后偷窃 3 号房屋(金额= 3)。 偷窃到的最高金额= 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋(金额= 2), 偷窃 3 号房屋(金额= 9),接着偷窃 5 号房屋(金额= 1)。 偷窃到的最高金额= 2 + 9 + 1 = 12 。
图片来源:https://github.com/azl397985856/leetcode
题目解析
还是房子,这次不是刷房子,而是抢房子。。。:)
条件和前面类似,就是相邻的房子不能抢。老样子,四个步骤走一遍:
问题拆解
如果我们要求解抢完 n 个房子所获得的最大收入,因为题目的要求,我们可以思考第 i 个房子是否应该抢,如果要抢,那么第 i - 1 个房子就不能抢,我们只能考虑抢第 i - 2 个房子。如果不抢,那么就可以抢第 i - 1 个房子,这样一来,第 i 个房子就和第 i - 1 个房子,以及第 i - 2 个房子联系上了。
状态定义
通过之前的问题拆解,我们知道,如果我们从左到右去抢房子,抢到当前房子可以获得的最大值其实是和抢到前两个房子可以获得的最大值有关,因此我们可以用dp[i] 表示抢到第 i 个房子可以获得的最大值
递推方程
如果我们抢第 i 个房子,那么我们就只能去考虑第 i - 2 个房子,如果不抢,那么我们可以考虑第 i - 1 个房子,于是递推方程就有了:
dp[i]=Math.max(dp[i-2]+nums[i],dp[i-1])
实现
因为第 i 个位置和前面的两个位置都有关,这个时候我们可以把状态多开一格,dp[0] 表示的是一个房子都不抢的状态,dp[1] 就是最左边的房子获得的最大价值,这个房子之前也没有其他的房子,直接抢即可。
参考代码
//@五分钟学算法 //www.cxyxiaowu.com publicintrob(int[]nums){ if(nums==null||nums.length==0){ return0; } intn=nums.length; int[]dp=newint[n+1]; dp[1]=nums[0]; for(inti=2;i<= n; ++i) { dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]); } return dp[n]; }打家劫舍II
LeetCode 第 213 号问题:打家劫舍II。
题目描述
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入:[2,3,2] 输出:3 解释:你不能先偷窃 1 号房屋(金额= 2),然后偷窃 3 号房屋(金额= 2), 因为他们是相邻的。
示例 2:
输入:[1,2,3,1] 输出:4 解释:你可以先偷窃 1 号房屋(金额= 1),然后偷窃 3 号房屋(金额= 3)。 偷窃到的最高金额= 1 + 3 = 4 。
题目解析
前面那道题目的 follow up,问的是如果这些房子的排列方式是一个圆圈,其余要求不变,问该如何处理。
房子排列方式是一个圆圈意味着之前的最后一个房子和第一个房子之间产生了联系,这里有一个小技巧就是我们线性考虑 [0, n - 2] 和 [1, n - 1],然后求二者的最大值。
其实这么做的目的很明显,把第一个房子和最后一个房子分开来考虑。实现上面我们可以直接使用之前的实现代码。
这里有一个边界条件就是,当只有一个房子的时候,我们直接输出结果即可。
参考代码
//@五分钟学算法 //www.cxyxiaowu.com publicintrob(int[]nums){ if(nums==null||nums.length==0){ return0; } if(nums.length==1){ returnnums[0]; } intn=nums.length; returnMath.max( robI(Arrays.copyOfRange(nums,0,n-1)), robI(Arrays.copyOfRange(nums,1,n)) ); } publicintrobI(int[]nums){ if(nums==null||nums.length==0){ return0; } intn=nums.length; int[]dp=newint[n+1]; dp[1]=nums[0]; for(inti=2;i<= n; ++i) { dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]); } return dp[n]; }
总结
序列类动态规划的系列问题还有很多,比如股票问题,这类问题通常会给你一个数组或者是字符串,在分析这些问题的时候,需要思考当前状态的选择是否要基于前面的状态,以及他们的关系是什么。
当然这里还有挺多的优化,比如动态规划的状态数组的空间优化,这些会在后面统一介绍,这里只需要熟悉动态规划的思考方向和方法即可。
-
矩阵
+关注
关注
1文章
441浏览量
35831 -
数组
+关注
关注
1文章
420浏览量
27122
原文标题:(再进阶版)有了四步解题法模板,再也不害怕动态规划!
文章出处:【微信号:TheAlgorithm,微信公众号:算法与数据结构】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
目标追踪的简易实现:模板匹配
专业技术指南——光模块故障判定排查法
四步检测降低83%故障率!大厂都在用的PCB质检流程
邮科工业交换机网络故障排查"望闻问切"四步法
山东零碳园区企业行动指南,四步抢占零碳红利
还在凭感觉做画像?GWI 利用大数据精准绘制核心客户群
AGV小车中的动态路径规划算法揭秘
有了这款智能标志桩图像监测装置, 再也不怕挖断电缆了

HarmonyOS5云服务技术分享--ArkTS调用函数
基于LockAI视觉识别模块:C++多模板匹配

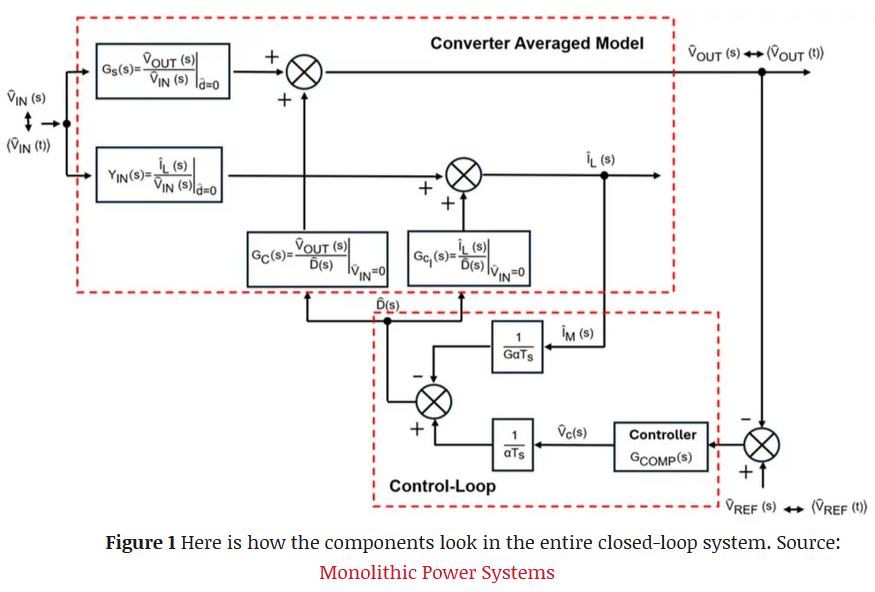
革新反激变换器设计:四步打造高稳定反馈回路补偿器,赋能EE工程师高效开发**
四线测电阻法





 有了四步解题法模板,再也不害怕动态规划!
有了四步解题法模板,再也不害怕动态规划!












评论