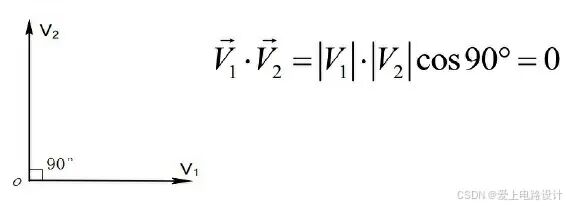数学-傅里叶级数的推导
本篇摘录“信号与系统3-傅里叶变换与频域分析”的小部分内容,作为正弦波生成的傅里叶级数展开法的补充。 1、矢量的正交分解 两矢量V1与V2正交,夹角为90°,那么两正交矢量的 内积为零 ,如下图所示。 图4.2.1 内积为零的原因 正交矢量集 :由两两正交的矢量组成的矢量集合。 非正交矢量的近似表示及误差 : 用与V2成比例的矢量c12V2近似地表示V1 ,则 误差矢量 : 显然,当两矢量V1与V2 正交 时,c12 = 0,即 。 矢量正交分解 :任意N维矢量可由N维正交
2025-10-09 关键字: 傅里叶级数
精品文章
更多>>推荐阅读
每月人物
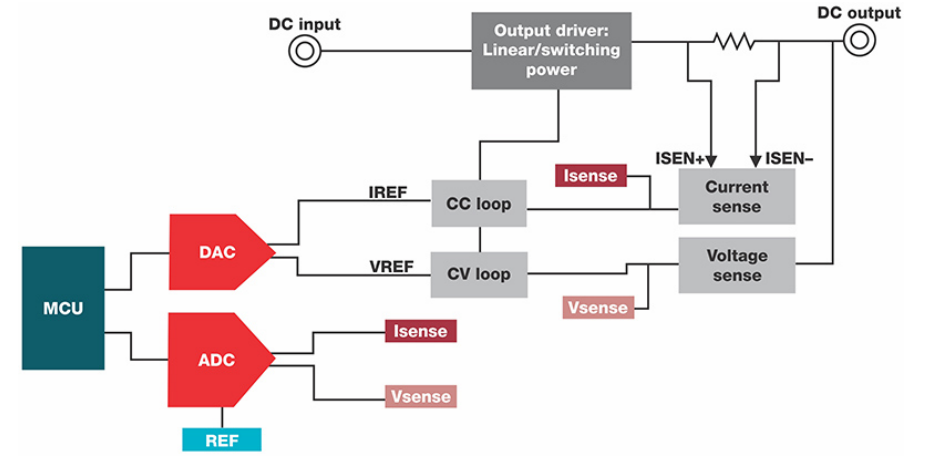
如何选用元器件实现精密直流电源的设计
电池测试、电化学阻抗谱和半导体测试等测试和测量应用需要准确的电流和电压输出直流电源。在环境温度变化为±5°C时,设备的电流和电压控制精度需要...

模拟大咖对话:国产替代之后的中国模拟芯出路何在?
(电子发烧友网报道 文/章鹰)9月中旬以来,电子时报报道,业内人士透露,随着交付周期延长到6个月以上,模拟芯片供应商德州仪器(TI)和安森美均已...
每周排行
创新实用技术专题