一文详解高速模数转换器的奈奎斯特规则

在上期中，我们探讨了如何限制 PFC 再浪涌电流。

本期，为大家带来的是《在高速转换器的奈奎斯特孔附近进行采样》，将介绍适用于超级奈奎斯特采样的高速模数转换器 (ADC) 奈奎斯特规则，如何使用抽取来协助频率规划，以及如何在设计和开发阶段设置保护频带，防止落入“频率空洞”。

频率规划是任何基于频率的应用中至关重要的部分。确保目标频率在频带范围内且有效，并避免降低到会损失伪波动态范围的程度，这应成为任何频率开发策略的一部分。在本文中，我们将介绍适用于超级奈奎斯特采样的高速模数转换器 (ADC) 奈奎斯特规则。我们还将介绍如何使用抽取来协助频率规划，以及如何在设计和开发阶段设置保护频带，防止落入“频率空洞”。

奈奎斯特规则

超级奈奎斯特采样、中频 (IF) 采样和二次采样在许多基于频率的应用中很常见，这些应用采用软件定义无线电 (SDR) 或类似雷达的接收器架构（请参阅图 1）。

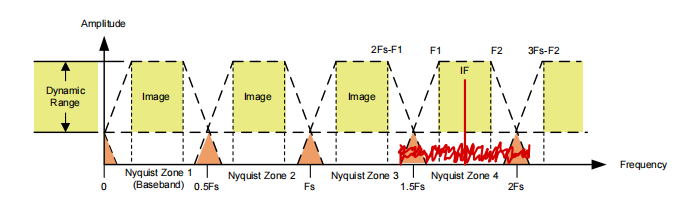
图 1：奈奎斯特采样与基带采样的关系示例（第一奈奎斯特）

在基带之外规划频率主要有两个原因（第一奈奎斯特）。第一个原因是获得抗混叠滤波器设计 (AAF)上的松弛限制（请参阅图 2）。最初，与更高奈奎斯特区域的滤波器设计相比，在设计基带滤波器时，一般滤波器滚降需要更陡。更陡的滤波器滚降会导致滤波器更复杂，从而使无源元件变得繁琐。它的物理原理很简单；您无法购买 0201 尺寸的 100µH 指示器。因此，当使用更高的奈奎斯特区域和可能更高的采样率时，对阻带区域滚降的权衡和要求会更加宽松，从而导致元件更少且元件尺寸更小。

使用高频率二次采样技术的第二个原因是在ADC前面放宽射频 (RF) 接收器信号链。假设 ADC 可以支持第一奈奎斯特区域之外的带宽要求（几乎总是如此），放宽接收器信号链可以消除射频信号链中的一个甚至两个混合级，从而使元件更少、噪声更少和复杂性更低。

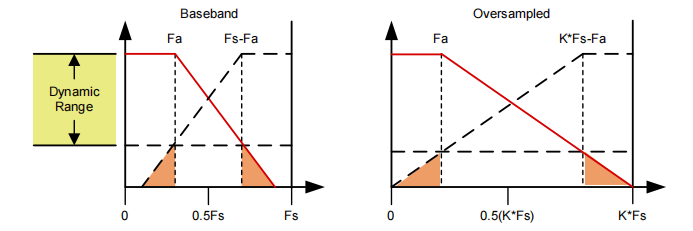
图 2：动态范围与 AAF 阻带衰减之间的关系

例如，图 3 展示了德州仪器 (TI) ADC3669相对于 500MSPS 采样频率 (FS) 对 800MHz 的中频进行采样。本质上，信号位于第四奈奎斯特区域。目标频率的图像或混叠会反射回第一奈奎斯特区域，显示为 200MHz 信号。大多数快速傅里叶变换 (FFT) 分析器（例如高速数据转换器专业版）只绘制第一奈奎斯特区域的 FFT 或 0Fs 到 0.5Fs。因此，如果目标频率高于 0.5Fs，图像会向下反射到第一个奈奎斯特区域或基带。如果伪波音调也在目标频带内，这可能会使事情变得更复杂。

那么，高于 0.5Fs 且仍然符合奈奎斯特标准的 ADC 采样如何呢？奈奎斯特规则规定信号的采样率必须等于或大于其带宽的两倍，以便保留信号的所有信息（请参阅方程式 1）：

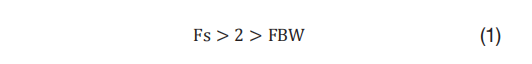
方程式 1

其中 Fs 是采样频率，FBW 是最大目标频率。

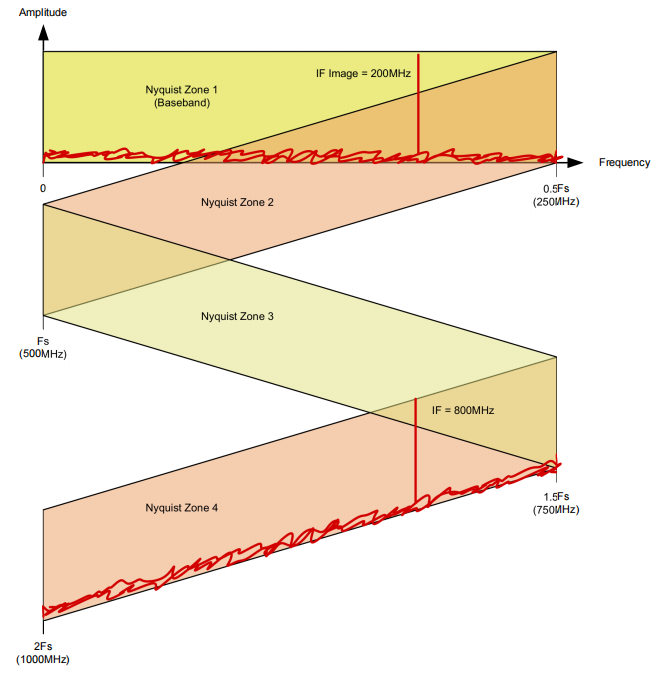
图 3：ADC3669 示例，其中 Fs = 500MSPS，中频 = 800MHz

保持奈奎斯特规则为正确的关键是目标频率的位置。只要信号不重叠并保持在单个奈奎斯特区域内，奈奎斯特标准仍然正确。唯一改变的是第一奈奎斯特区域的位置到更高的区域。中频采样因为这些权衡正变得非常流行。

什么是过程增益？

早期形式的高速信号链系列包括用于每单通道消耗瓦特功率的 ADC，以及用于捕捉、过滤并将所有转换器数据处理为某种有用格式的FPGA（现场可编程门阵列）。大多数设计人员会使用一种称为过程增益的方法。这种方法不仅通过消除不必要的伪波和噪声来帮助进行频率规划，而且能够通过限制奈奎斯特区域内处理的带宽来“增加”信噪比 (SNR) 方面的动态范围。将过程增益校正因子添加到标准 SNR 公式可得到方程式 2：

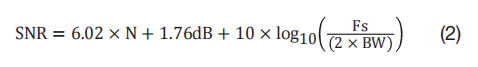
方程式 2

其中，N 是 ADC 位数，Fs 是 ADC 采样率，BW 是奈奎斯特区域内的相关带宽。

由于将更小的过程节点部署到 ADC 和数模转换器技术中，现在许多标准 FPGA 数字特性都驻留在 ADC 中。一些示例包括数字降压转换器 (DDC)、数控振荡器 (NCO) 和跳频。这些特性可显著帮助减轻 FPGA 处理的负载，从而可以在其他地方使用其内部资源。

为什么要进行频率规划？

在使用 ADC 设计系统时，适当的频率规划是一个重要步骤。频率规划可确保高效利用 ADC 的动态范围，并最大限度地减少不必要的伪波信号，这对于如 SDR 系统或高密度射频信号链等高性能应用至关重要。

频率规划的一个重要方面是优化ADC的动态范围。模拟域中的每个额外信号都会占用 ADC 的可用输入信号功率预算，从而降低整体动态范围能力。适当的频率规划可以确保 ADC 充分发挥其功能，方法是策略性地放置输入频率以尽可能扩大可用的动态范围。该方法需考虑不必要的伪波和谐波在采样带中出现的位置，确保目标信号与伪波元件之间没有重叠。

另一个关键方面是管理由 ADC 生成的固有伪波信号，例如谐波和交错伪影。当这些伪波成分保持在预期频带之外时，频率规划即为成功，尤其是在数据采样后未采用数字滤波的系统中。频率规划还有助于更大限度地减小与时钟相关的伪波的影响，例如来自缺乏通道隔离的时钟器件的伪波。这些伪波在使用高密度时钟分配解决方案的大型元件系统中尤其成问题。

在包含交错 ADC的系统中，还需要考虑交错伪波管理，在该系统中，多个 ADC 内核以正交方式对公共输入信号进行采样，从而将采样率和奈奎斯特区域有效地加倍。但是，这种交错会在 Fs/2-Fin 处引入伪波音调。此外，在使用更高交错因子的系统中，这一相同的 Fs/2-Fin 伪波会被“新”的 Fs/2-Fin 再次调制。这会导致新 Fin 由交错 Fs/2-Fin 伪波组成，这意味着引入的伪波计数远高于单个交错因子。频率规划使您能够通过利用模拟滤波或（首选）数字抽取滤波器来缓解这些伪波，从而不必设计复杂的模拟信号链即可显著衰减伪波。虽然这种方法会降低所选区域的瞬时带宽，但它确保了更好的动态范围和更清晰的信号性能。

频率规划的常见缺陷

尽管有优势，但可能存在不合理的频率计划，这会导致ADC 性能下降的问题。一个常见的挑战是奈奎斯特区域重叠。规划不当的输入信号可能会落入奈奎斯特区域的边界，从而产生混叠效应，进而降低系统性能。为防止这种情况发生，必须在适当的频带内分配信号，以在考虑的奈奎斯特区域内保持频谱完整性。

时钟伪波污染是另一个常见问题，尤其是在使用低质量时钟器件或时钟分配欠佳的系统中。这些调制到 ADC 频谱的伪波信号可以通过提供已知的偏移伪波来严重影响敏感应用。精心设计时钟基础设施（包括使用更高质量的时钟解决方案）有助于减轻这些影响。另一种可能的方法是在该偏移频率下使用高位频带抑制滤波器对数据进行数字滤波，尽管如果实施不当，任何有用的信号都将随伪波一起被删除。

要克服的另一个挑战是改正严格调制的三阶互调失真伪波。这些伪波几乎总是落在通带内，并且通常是限制无伪波动态范围的伪波。如果抽取因子非常高，则这些音调可能会处于衰减频带内。但是，对于大多数多音系统来说，这不太可能，因为多音系统本身需要比单音系统更大的瞬时带宽，因此无法集成这样的大型抽取滤波器。

最后，您必须在带宽和动态范围之间进行权衡。虽然抽取可以抑制伪波元件和谐波，但代价是瞬时带宽会降低。对于实现针对特定应用要求的出色性能而言，平衡这些权衡至关重要。

使用抽取进行适当频率规划的优势

有效的频率规划具有多种优势，可增强接收器系统设计。一个优势是改进了伪波抑制。数字抽取滤波器可以有效地衰减伪波，通常可实现约 -85dBFS 的抑制水平，从而带来更清晰的信号性能，并更好地利用预期信号的 ADC 动态范围，而非带外伪波噪声。

另一个优势是降低了 ADC 的数据吞吐量。通过抽取来降低 ADC 的输出数据速率，您可以将 ADC 与速度更低、尺寸更小、更具有成本效益的 FPGA 连接。这种传输数据的减少不仅简化了硬件要求，还使系统能够在双频带或四频带中运行，从而同时对多个射频频带进行采样。

在 ADC 上使用抽取的另一个显著优势是，系统能够单独在软件中完全重新配置。您可以规划 ADC 和 FPGA 之间的硬件接口以支持系统的预期最大数据速率，从而能够以较低的数据速率或更窄的带宽运行许多其他系统。软件可重新配置的系统对于需要在多种场景中部署的应用特别有用。

资源节省也是有效频率规划的一个显著成果。由于需要更少的输出通道（无论是高速串行数据通道还是低电压差分信号对），您可以节省 ADC 和 FPGA 上的宝贵引脚，从而提高利用率。这在印刷电路板面积和功率受限的高通道系统中尤其重要。

理论示例：利用抽取功能规划频率

考虑交错 ADC 以 Fs 采样一个常规射频输入信号。交错过程会在 Fs/2-Fin 处引入伪波，可能会干扰预期信号。通过应用 2 倍抽取滤波器（如图 4 所示），可以将此伪波衰减到抽取滤波器的抑制限值范围内。此外，抽取过程可降低 ADC 的输出数据速率，从而实现具有成本效益的 FPGA 连接并简化下游处理。此外，由于 SNR 中的 N（即噪声）减半，而 S（即信号）保持不变，宽带噪声的降低会带来约 3dB 的过程增益。

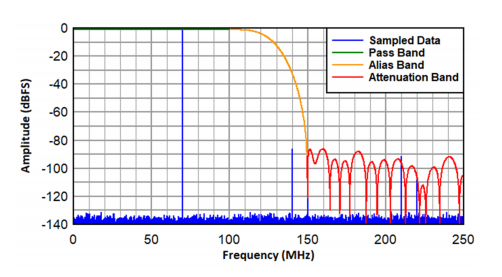
图 4：500MSPS 且 70MHz FIN（抽取因子为 2）条件下理论数据的抽取滤波器响应

实际案例：利用抽取功能规划频率

在 ADC 上使用抽取可简化频率规划过程，因为降低采样率可有效地缩小目标带宽。将抽取视为有选择地集中在频谱的较窄部分。通过专注于较窄的频带，更多不需要的谐波或伪波最终会落在目标通带之外，进而被滤除。以下示例使用ADC3669来演示在进行频率规划时抽取产生的差异。图 5 显示了一个传统的频谱采集，此时 ADC 未使用大小为 16384 点的 FFT 执行抽取。您可以看到，不需要的谐波在频带内，对性能产生了负面影响。

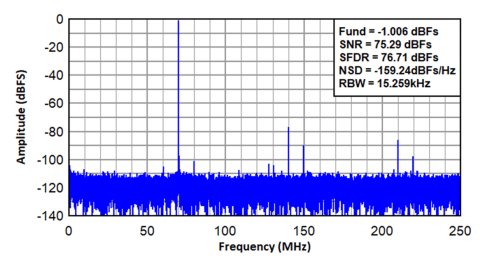
图 5：ADC3669 在 500MSPS 且接近 70MHz FIN（无抽取）时采集的实际频谱。

这些谐波可能是ADC 或一些外部模拟频率造成的附加噪声。图 6 显示了 ADC 处于实时抽取模式（抽取因子为 2）时的示例。您可以看到不需要的谐波伪波现在会出现在频带外并通过抽取滤波器滤除。请注意，由于过程增益而额外提高了 +3dB。

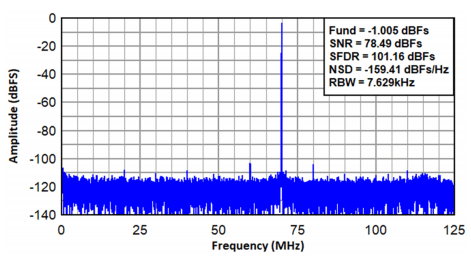
图 6：ADC3669 在 500MSPS 且接近 70MHz FIN（抽取因子为 2）时采集的实际频谱

此外，FFT 的分辨率带宽实际上也减小了 2 倍，因为我们为 FFT 计算保持相同的点数。这有助于将模拟频率解析为更密集的频段。到目前为止，我们只讨论了实数抽取，它仅对数据进行滤波，不涉及频率移位。如果您的目标信号在您每次抽取时降至 Fs/4 以下，则实数抽取非常有用。但是，如果您想抽取超出此范围的信号，该怎么办？目标信号通常不以零频率（基带）为中心，而是以某个中频为中心。这时就需要使用复数抽取。具有较新数字特性（例如ADC3669）的 ADC 在复数 DDC 级中包含NCO 混频器。将目标信号与 NCO 频率混合会在抽取之前将信号移动到基带，使您能够利用在器件带宽内任何位置抽取信号的优势。

图 7 显示了ADC3669在复数抽取模式（抽取因子为 64）下的采集结果，当使用 8192 点计算 FFT 时，产生的有效采样带宽为 7.8125MHz。输入频率为 70MHz，而 NCO 频率为 71MHz。当信号与 NCO 频率混合时，信号会移位至基带，从而产生约 -1MHz 的音调。

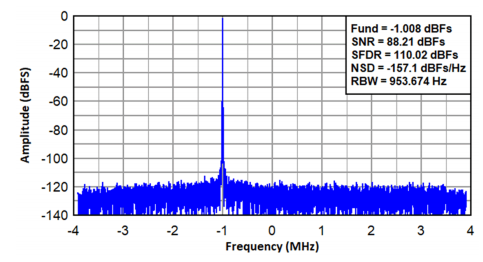
图 7：ADC3669 在 500MSPS 且抽取因子为 64 时采集的复合频谱（FIN=70MHz，Fnco=71MHz）

ADC3669可采集抽取因子高达 32768 的窄带，这对于具有高密度射频频带或紧凑通道间距的应用非常有用。通过如此高的因子抽取可以放大您的目标信号，滤除几乎所有其他内容。现代 ADC（例如 ADC3669）提供的抽取因子范围使频率规划具有更高的灵活性，因为可用更轻松地滤除不需要的伪波。图 8 显示了一个抽取因子为 16384 的采集，使用 8192 个 FFT 点计算，分辨率带宽为 3.726Hz。即使伪波在基频的几千赫兹以内，您也可以轻松地以高抽取率将其滤除。

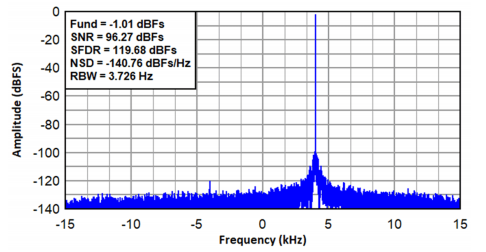
图 8：ADC3669 在 500MSPS 且抽取因子为 16384 时采集的复合频谱（FIN=70MHz，Fnco=69.996MHz）

由于NCO 频率比输入信号低 4kHz，因此降频转换信号出现在正频率偏移处。在此抽取模式下以 500MSPS 运行时，此 ADC 可以在 30.517kHz 范围内以可编程 NCO 频率对信号进行采样。

结语

频率规划是基于 ADC 的系统设计的重要方面，解决了伪波管理、动态范围优化和AAF 设计以及高效数据处理等挑战。通过预先实施周密的频率规划，您可以避免奈奎斯特区域重叠和时钟伪波污染等常见缺陷，同时受益于改进的伪波抑制和动态范围、ADC 数字接口或数据速率降低，以及 FPGA 资源节约等优势。通过仔细权衡这些利弊和利用 ADC 抽取等特性，可以为一系列应用实现高性能、软件可重新配置的接收器系统，同时避免出现下一个采样空洞。