comsol电磁场仿真案例

COMSOL公司是全球多物理场建模与仿真解决方案的提倡者和领导者，其旗舰产品COMSOL Multiphysics，使工程师和科学家们可以通过模拟，赋予设计理念以生命。它有无与伦比的能力，使所有的物理现象可以在计算机上完美重现。COMSOL的用户利用它提高了手机的接收性能，利用它改进医疗设备的性能并提供更准确的诊断，利用它使汽车和飞机变得更加安全和节能，利用它寻找新能源，利用它探索宇宙，甚至利用它去培养下一代的科学家。

Multiphysics翻译为多物理场，因此这个软件的优势就在于多物理场耦合方面。多物理场的本质就是偏微分方程组（PDEs），所以只要是可以用偏微分方程组描述的物理现象，COMSOL Multiphysics都能够很好的计算、模拟、仿真。

COMSOL Multiphysics是一款大型的高级数值仿真软件。广泛应用于各个领域的科学研究以及工程计算，模拟科学和工程领域的各种物理过程。

COMSOL Multiphysics是以有限元法为基础，通过求解偏微分方程（单场）或偏微分方程组（多场）来实现真实物理现象的仿真，用数学方法求解真实世界的物理现象。

大量预定义的物理应用模式，范围涵盖从流体流动、热传导、到结构力学、电磁分析等多种物理场，用户可以快速的建立模型。COMSOL中定义模型非常灵活，材料属性、源项、以及边界条件等可以是常数、任意变量的函数、逻辑表达式、或者直接是一个代表实测数据的插值函数等。

预定义的多物理场应用模式， 能够解决许多常见的物理问题。同时，用户也可以自主选择需要的物理场并定义他们之间的相互关系。当然，用户也可以输入自己的偏微分方程（PDEs），并指定它与其它方程或物理之间的关系。

COMSOL Multiphysics力图满足用户仿真模拟的所有需求，成为用户的首选仿真工具。它具有用途广泛、灵活、易用的特性，比其它有限元分析软件强大之处在于，利用附加的功能模块，软件功能可以很容易进行扩展。

COMSOL的磁场仿真分析

真空中的平面电磁波

电磁场若要符合麦克斯韦方程，则该电磁场的场矢量E和B之间必存在某种联系，且电场可以脱离电荷和电流单独存在，并以有限的速度在空间传播。现在我们从麦克斯韦方程出发，从理论上分析存在于真空中的电磁场所具有的性质。

我们讨论不存在实物的真空，从t=0时刻起，该空间不存在传导电流。没有电荷流动意味着该空间或无电荷分布和电荷分布不随时间变化。不随时间变化的电荷产生的是静态电场，而在这里我们不研究静态场，故不妨假设电荷和电流都不存在，这样的空间称为自由空间。因自由空间中

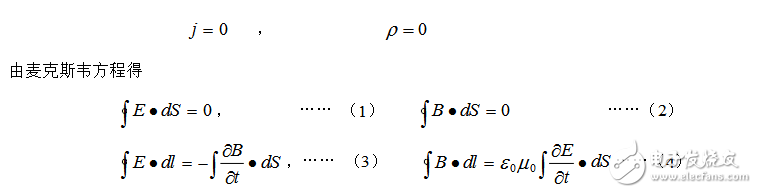
其中（1）表示自由空间中的电场是无源场，电场线是无头无尾的闭合曲线，或是从无限远处来，延伸到无限远去的曲线。（2）表示自由空间的磁场仍是无源场，磁场的磁感应线仍是无头无尾的闭合曲线。（3）表示自由空间的电场是有旋场，变化的磁场是涡旋的中心，在磁感强度变化的地方，周围有闭合的电场线。（4）表示自由空间中的磁场是有旋场，只有变化的电场才是磁场的漩涡中心，在电场强度变化的地方，周围存在闭合的磁感应线。

我们不难从这四个积分式子中得到他们的微分形式

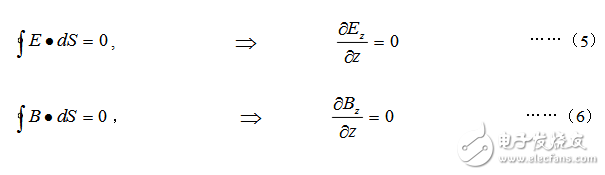
可以看出电矢量和磁矢量满足的方程式具有相同的形式，式中的常量是恒正的，我们用另一个恒量表示之，令

上面两个式子式沿z方向传播的简谐波。和k是两个常量，不能完全任意，它们的值必须保持这两个列简谐波是波动方程的解，E和B是电场波与磁场波的初相位。

二、 通过GUIDE进行仿真

使用GUIDE画出（14）（15）式的解析解的动画图形、解析解的瀑布图形和数值解的图形，（16）（17）

式的沿z方向传播的简谐平面电磁波。

打开GUIDE的设计窗口，在GUIDE的设计窗口中画一个坐标轴，三个单选按钮，四个静态文本框，三个编辑框和一个按钮。并对这些进行相应的属性设置，如图4所示是一个已经做好的fig文件。

在编程之前必须对三个单选按钮进行如下编程

function radiobutton1_Callback（hObject， eventdata， handles）

set（handles.radiobutton1，‘value’，1）;

set（handles.radiobutton2，‘value’，0）;

set（handles.radiobutton3，‘value’，0）;

function radiobutton2_Callback（hObject， eventdata， handles）

set（handles.radiobutton1，‘value’，0）;

set（handles.radiobutton2，‘value’，1）;

set（handles.radiobutton3，‘value’，0）;

function radiobutton3_Callback（hObject， eventdata， handles）

set（handles.radiobutton1，‘value’，0）;

set（handles.radiobutton2，‘value’，0）;

set（handles.radiobutton3，‘value’，1）;

这样可以使单选按钮选中其中的一个，其他的按钮不起作用。

因为程序中有三套程序，每一个按钮对应着一套程序。选中一个按钮只有一套程序起作用。这样通过一个if…elseif…else来完成这项任务。

1、解析解的动画图形

我们可以看出（14）和（15）式在形式上是一样的，只不过是方向不一样，电矢量E和磁矢量B相互垂直。它们都与弦震动方程

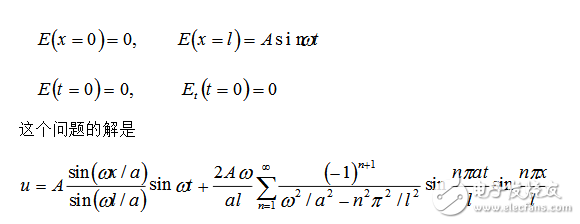
可以用动画来表现这个解，下面是一段由上式编写的程序。

clear

a=1;l=1;

A=0.01;w=6;

x=0:0.5:1;

t=0:0.001:4.3;

［X，T］=meshgrid（x，t）;

u0=A*si

n（w*X./a）.*sin（w.*T）/sin（w*l/a）; u=0;

for n = 1:100;

uu=（-1）^（n+1）*sin（n*pi*X/l）.*sin（n*pi*a*T/l）/（w*w/a/a-n*n*pi*pi/l/l）;

u=u+uu; end

u=u0+2*A*w/a/l.*u; figure（1）

axis（［0，1，-0.05，0.05］）

h=plot（x，u（1，：），‘linewidth’，3）;

set（h，‘erasemode’，‘xor’）;

for j=2:length（t）;

set（h，‘ydata’，u（j，：））;

axis（［0，1，- 0.05，0.05］）

drawnow end figure（2）

waterfall（X（1:50:3000，：），T（1:50:3000，：），u（1:50:3000，：））

xlabel（‘x’）

ylabel（‘t’）

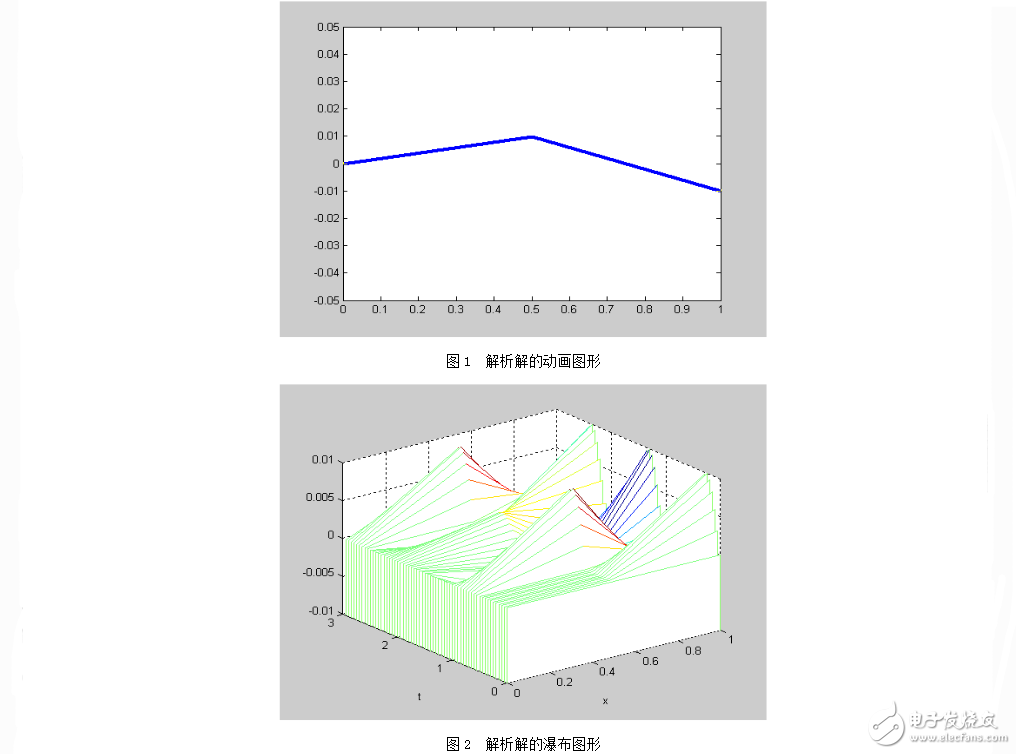
图1是动画中的一幅画面，可以看出，固定端一直保持不动，而作谐振动的端使弦也产生了一种在传播的振动。这相当于将一根绳的一端固定，而周期性的摆动另一端时，在绳上所产生的运动。［3］

2、数值解的图形

我们再用微分方程工具箱求解上面的问题。我们用二维图形来表示一维的弦，让弦的侧面不受力，左端固定，右端作受迫振动。

在Options/Axes limits下选择x轴范围为0～1，y轴范围为0～1.以原点为顶点画一个场为1宽为0.4的矩形，矩形的顶点为（0，0），（1，0），（1，0.4），（0，0.4）。

按照题意，矩形的右边界是齐次的狄里克利边界条件，可取h=1，r=0，左边界是非齐次的狄里克利边界条件，可取h=1，r=0.01*sin（6*t），上下边界则取齐次的诺依曼边界条件，即g=0，q=0。

方程的设置是hyperbolic型，系数是c=1，a=0，f=0，d=1. 为了有足够的精度，初始化的网格要再作两次细分。

在解方程的参数设置对话框Solve Parameters中，各项选择如下：在Plot type下，选Color和Height（3-D Plot），在Property下，对应的位置中都选User entry，在User entry下，再在相应的位置都输入10*u，这样做的目的是，弦的振幅太小，为了达到更好的显示效果，所以将振幅放大10倍来画图。所得的图形如

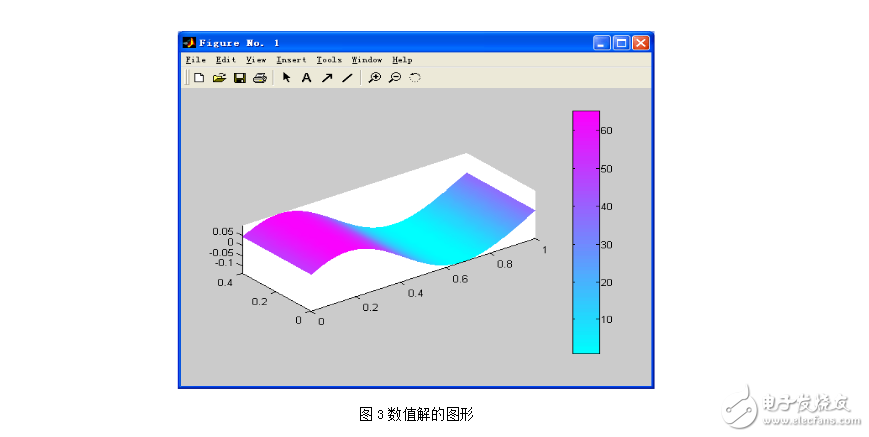
3、沿z方向传播的简谐平面电磁波

通过（16）（17）式进行如下编程

a = str2double （get（handles.t， ‘string’））;

for t=1:a;

v=2;

w= str2double （get（handles.w， ‘string’））;

k=0:1：40;

y=sin（w*（t-k/v））;

x=zeros（1，41）;

z=k stem3（z，x，y，‘r’）;

hold on x=sin（w*（t-k/v））;

y=zeros（1，41）;

z=k;

stem3（z，x，y，‘b’，‘filled’）;

view（-37.50，30）;

hold off w1=moviein（a）;

w1（：，t）=getframe;

xlabel（‘t’）;

ylabel（‘E’）;

zlabel（‘B’）;

title（‘沿Z方向传播的简谐平面电磁波’）

end

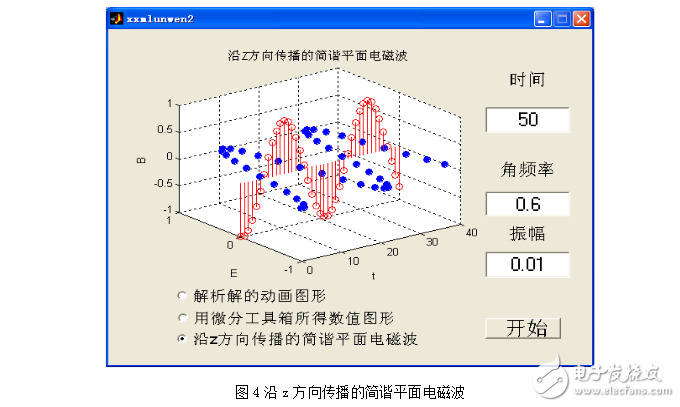
这时可以得到function pushbutton1_Callback（hObject， eventdata， handles）下面的程序

if （findobj（‘tag’，‘radiobutton1’，‘value’，1））;

a=1;

l=1;

A= str2double （get（handles.b， ‘string’））;

w= str2double （get（handles.w， ‘string’））;;

x=0:0.5:1; t=0:0.001:4.3;

［X，T］=meshgrid（x，t）;

u0=A*sin（w*X./a）.*sin（w.*T）/sin（w*l/a）;

u=0;

for n = 1:100;

uu=（-1）^（n+1）*sin（n*pi*X/l）.*sin（n*pi*a*T/l）/（w*w/a/a-n*n*pi*pi/l/l）;

u=u+uu; end

u=u0+2*A*w/a/l.*u; figure（1）

axis（［0，1，-0.05，0.05］）

h=plot（x，u（1，：），‘linewidth’，3）;

set（h，‘erasemode’，‘xor’）;

for j=2:length（t）;

set（h，‘ydata’，u（j，：））;

axis（［0，1，- 0.05，0.05］） drawnow end figure（2）

waterfall（X（1:50:3000，：），T（1:50:3000，：），u（1:50:3000，：））

xlabel（‘x’）

ylabel（‘t’）

elseif （findobj（‘tag’，‘radiobutton2’，‘value’，1））;

% function pdemodel

［pde_fig，ax］=pdeinit;

pdetool（‘appl_cb’，1）;

set（ax，‘DataAspectRatio’，［1 1.5 1］）;

set（ax，‘PlotBoxAspectRatio’，［1 0.66666666666666663 2］）;

set（ax，‘XLim’，［0 1］）; set（ax，‘YLim’，［0 1］）;

set（ax，‘XTickMode’，‘auto’）;

set（ax，‘YTickMode’，‘auto’）;

% Geometry description：

pderect（［0 1 0.40000000000000002 0］，‘R1’）;

set（findobj（get（pde_fig，‘Children’），‘Tag’，‘PDEEval’），‘String’，‘R1’）

% Boundary conditions：

pdetool（‘changemode’，0）

pdesetbd（4，。。。

‘dir’，。。。

1，。。。

‘1’，。。。

‘0.01*sin（6*t）’）

pdesetbd（3，。。。

‘neu’，。。。

1，。。。

‘0’，。。。

‘0’）

pdesetbd（2，。。。 ‘dir’，。。。 1，。。。 ‘1’，。。。 ‘0’）

pdesetbd（1，。。。 ‘neu’，。。。 1，。。。 ‘0’，。。。 ‘0’）

% Mesh generation：

setuprop（pde_fig，‘Hgrad’，1.3）;

setuprop（pde_fig，‘refinemethod’，‘regular’）; pdetool（‘initmesh’） pdetool（‘refine’） pdetool（‘refine’） % PDE coefficients： pdeseteq（3，。。。 ‘1.0’，。。。 ‘0.0’，。。。 ‘0.0’，。。。 ‘1.0’，。。。 ‘0:0.1:1.5’，。。。 ‘0.0’，。。。 ‘0.0’，。。。 ‘［0 100］’）

setuprop（pde_fig，‘currparam’，。。。 ［‘1.0’;。。。 ‘0.0’;。。。 ‘0.0’;。。。 ‘1.0’］）

% Solve parameters：

setuprop（pde_fig，‘solveparam’，。。. str2mat（‘0’，‘3168’，‘10’，‘pdeadworst’，。。. ‘0.5’，‘longest’，‘0’，‘1E-4’，‘’，‘fixed’，‘Inf’）） % Plotflags and user data strings：

setuprop（pde_fig，‘plotflags’，［1 1 4 1 1 1 1 1 0 0 1 16 1 0 1 0 0 1］）; setuprop（pde_fig，‘colstring’，‘’）; setuprop（pde_fig，‘arrowstring’，‘’）; setuprop（pde_fig，‘deformstring’，‘’）; setuprop（pde_fig，‘heightstring’，‘10*u’）; % Solve PDE： pdetool（‘solve’）

else （findobj（‘tag’，‘radiobutton3’，‘value’，1））; a = str2double （get（handles.t， ‘string’））; for t=1:a; v=2;

w= str2double （get（handles.w， ‘string’））; k=0:1：40; y=sin（w*（t-k/v））; x=zeros（1，41）; z=k stem3（z，x，y，‘r’）; hold on x=sin（w*（t-k/v））; y=zeros（1，41）; z=k;

stem3（z，x，y，‘b’，‘filled’）; view（-37.50，30）; hold off w1=moviein（a）; w1（：，t）=getframe; xlabel（‘t’）; ylabel（‘E’）; zlabel（‘B’）;

title（‘沿Z方向传播的简谐平面电磁波’） end

end grid on

通过运行GUIDE就会得道图1、图2、图3和图4.

三、 结论

MATLAB有强大的求解偏微分方程和可视化功能模拟各类物理场的实验是成功的。借助偏微分方程工具箱，可以通过分析静电学、电场、磁场和电磁场的原理而建立微分方程，经过数值计算模拟各类电磁场问题。使问题更加形象逼真。 利用这些特性及GUI 功能可以实现交互式数据处理。图形用户界面的设计确定了应用程序的主要框架和基本功能，完成了窗口、图标、按钮等用户界面，软件开发者只需在由软件发工具自动生成的程序代码中添加自己的运算或控制代码，就可以完成自己的设计。