支路电流法适用于非线性电路吗

支路电流法（Node Voltage Method）是一种在电路分析中常用的方法，主要用于求解线性电路中的电流和电压。然而，对于非线性电路，支路电流法的应用会受到一定的限制。

1. 支路电流法的基本原理

支路电流法是一种基于基尔霍夫电流定律（KCL）的电路分析方法。基尔霍夫电流定律指出，在一个电路节点上，流入节点的电流之和等于流出节点的电流之和。通过将电路分解为若干个支路，并在每个节点上应用基尔霍夫电流定律，可以列出一组线性方程组，进而求解电路中的电流和电压。

2. 非线性电路的特点

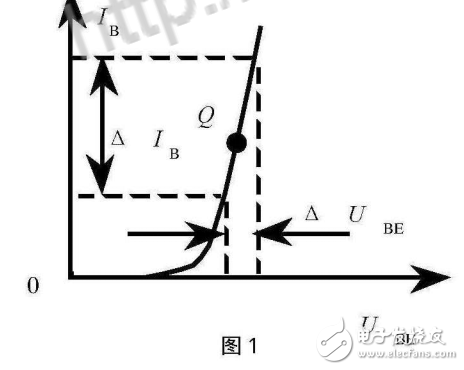
非线性电路是指电路元件的电压-电流关系不是线性的，即元件的电阻、电容或电感等参数与电流或电压的关系不是简单的正比关系。常见的非线性元件包括二极管、晶体管、运算放大器等。非线性电路的特点是：

• 电压-电流关系复杂，可能具有非线性、非对称性或非单调性等特点。
• 电路的稳态和瞬态响应可能具有非线性特性，如谐振、振荡等。
• 电路的分析和设计更加复杂，需要考虑非线性元件的非线性特性。

3. 支路电流法在非线性电路中的应用

虽然支路电流法主要用于线性电路的分析，但在某些情况下，也可以应用于非线性电路的分析。以下是一些可能的应用场景：

3.1 线性化处理

对于某些非线性元件，可以通过线性化处理将其转化为线性元件。例如，对于二极管，可以在其工作点附近进行泰勒展开，保留一阶项，忽略高阶项，从而将其视为线性元件。然而，这种方法只适用于元件工作在近似线性的区域，对于大信号或强非线性元件，线性化处理可能不够准确。

3.2 小信号分析

对于非线性电路，可以采用小信号分析的方法，即在电路的稳态工作点附近进行线性化处理，分析电路的小信号响应。这种方法适用于分析电路的稳定性、频率响应等特性。然而，小信号分析无法反映电路的大信号行为和非线性特性。

3.3 迭代求解

对于复杂的非线性电路，可以采用迭代求解的方法。首先，假设电路中的非线性元件为线性元件，求解电路的初始解。然后，根据初始解计算非线性元件的实际工作状态，更新电路的参数。重复这个过程，直到满足一定的收敛条件。这种方法可以求解非线性电路的稳态和瞬态响应，但计算过程可能较为复杂。

4. 支路电流法在非线性电路分析中的挑战

尽管支路电流法在某些情况下可以应用于非线性电路的分析，但在实际应用中，仍然面临一些挑战：

4.1 非线性元件的建模难度

非线性元件的电压-电流关系复杂，难以用简单的数学模型描述。对于强非线性元件，如二极管、晶体管等，需要采用更复杂的模型，如二极管方程、Ebers-Moll模型等，这增加了电路分析的难度。

4.2 非线性方程的求解难度

非线性电路的方程组可能具有多个解，甚至可能没有解。求解非线性方程组需要采用特殊的数值方法，如牛顿法、拟牛顿法等，这些方法的计算复杂度较高，收敛速度可能较慢。

4.3 稳定性和收敛性问题

在非线性电路的分析过程中，可能遇到稳定性和收敛性问题。例如，在迭代求解过程中，可能存在多个稳定点，导致求解过程陷入局部最优解。此外，非线性电路的瞬态响应可能具有振荡、混沌等复杂现象，增加了分析的难度。

5. 解决方案

针对支路电流法在非线性电路分析中遇到的挑战，可以采取以下解决方案：

5.1 选择合适的非线性模型

根据非线性元件的特性和电路的工作条件，选择合适的非线性模型。对于简单的非线性元件，可以采用线性化处理或小信号分析；对于复杂的非线性元件，需要采用更精确的非线性模型。

5.2 采用高效的数值方法

在求解非线性方程组时，可以采用高效的数值方法，如牛顿法、拟牛顿法等。这些方法可以提高求解速度，提高收敛性。同时，可以采用多尺度方法、同伦方法等，以提高求解的稳定性和准确性。

5.3 引入辅助变量和约束条件

在非线性电路的分析过程中，可以引入辅助变量和约束条件，以简化问题。例如，可以引入电流源、电压源等辅助元件，将非线性电路转化为线性电路；或者引入功率平衡、能量守恒等约束条件，以限制电路的工作状态。