Other Parts Discussed in Post: CONTROLSUITE, POWERSUITE, SFRA
作者:Hardy Zhou
TI C2000在数字电源领域有很广法的应用,同时针对数字电源控制器的设计提供了CONTROLSUITE 的DPlib的软件库,可以很容易实现PID, 2P2Z, 3P3Z等控制器的软件代码设计,同时也提供PowerSUITE的Compensation Designer GUI来实现控制器的可视化设计以及获得离散化参数供C2000数字设计. 本文以DPLib中的2P2Z控制器设计为例,来说明C2000 Compensation Designer GUI中的 2P2Z控制器参数对应到的实际S域传递函数实际表达式,为2P2Z以及其他形式的控制器的理解、开发和调试带来很大的便利.
1.Compensation Designer和传统的 2P2Z控制器的S域表达式对比
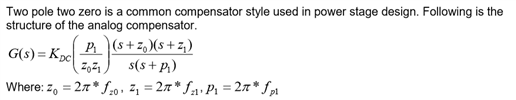
而我们常看到的2P2Z控制器S域的传递函数模型一般如下:
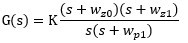
K表示控制器增益,Wz0和Wz1是两个零点,Wp1是第二个极点, 同样有:
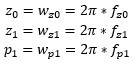
所以可以看到传统2P2Z控制器S域传递函数的增益K跟Compensation Designer中的S域传递函数增益关系式子如下.
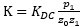
2.Compensation Designer和DPLib中2P2Z控制器离散化表达式
Compensation Designer中2P2Z控制器双线性变换离散化模型为:

由这个表达式可以看出,由于零极点和数字控制频率FS的单位都是KHz,把 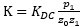 增益的表达式独立出来,传递函数的分子和分母都是以频率相除得到的值,所以实际计算,可以简单用KHz为单位来表达频率的量值.
增益的表达式独立出来,传递函数的分子和分母都是以频率相除得到的值,所以实际计算,可以简单用KHz为单位来表达频率的量值.
DPLib中2P2Z控制器双线性变换离散化模型为

我们可以看到分母的系数符号是取反了,因为C2000 DPLib计算2P2Z控制器输出表达式是,
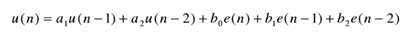
这跟2P2Z离散函数一般表达式 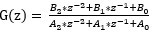 有差别.
有差别.
所以分母的,取反了, 这点要非常注意,不然容易在使用过程中,出现Z域到S域的变换得不到正确的S域公式,也会造成设计控制器模型出现问题.
3.两个离散化传递函数的统一
令 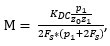 我们可以获得
我们可以获得
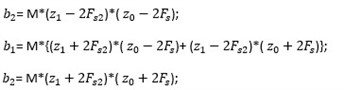
同理可以获得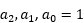 的表达式.
的表达式.
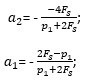
注意 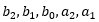 在Compensation Designer GUI中生成的B2,B1,B0,A2,A1是完全对应的.
在Compensation Designer GUI中生成的B2,B1,B0,A2,A1是完全对应的.
4.Compensation Designer 2P2Z控制器S域和Z域传递函数的解析
2P2Z控制器的S域传递函数表达式在章节1已经有说明,KDC以增益dB的形式表达, KDC转化为实际参数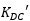 的表达式如下:
的表达式如下:
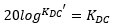
实际增益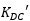 为:
为:
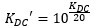
实际2P2Z控制器的S域传递函数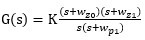 增益是
增益是
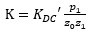
把Compensation Designer 的零极点频率,转化为单位Hz和角频率,代入G(s)表达式,就可以获得实际系统的传递函数.
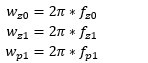
下面的以Compensation Designer中的2P2Z控制器设计为例进行说明如何获得s域传递函数的表达式.
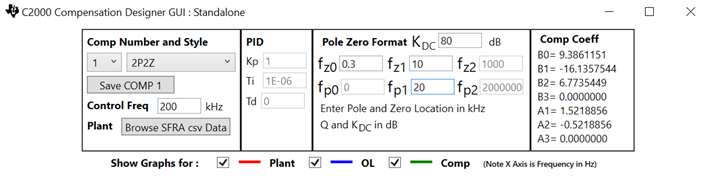
S域传递函数的增益
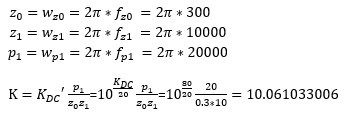
所以可以得到S域中的传递函数是
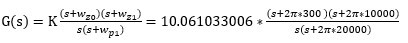
使用matlab求s域到z域(离散时间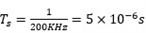 ,双线性变换Tustin
,双线性变换Tustin 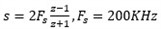 ,), 就可以获得跟Compensation Designer GUI里面相同的B0,B1,B2,A0,A1,A2参数, 这样也可以验证我们的推导是正确的.
,), 就可以获得跟Compensation Designer GUI里面相同的B0,B1,B2,A0,A1,A2参数, 这样也可以验证我们的推导是正确的.
审核编辑:金巧
-
控制器
+关注
关注
114文章
17643浏览量
190261 -
嵌入式处理
+关注
关注
0文章
341浏览量
10450 -
GUI
+关注
关注
3文章
693浏览量
42851 -
DPL
+关注
关注
0文章
2浏览量
13144
发布评论请先 登录
onsemi三电平ANPC Q2Pack模块:NXH800A100L4Q2F2S1G/P1G与NXH800A100L4Q2F2S2G/P2G的详细解析

探索 NXH80T120L2Q0S2G/S2TG, NXH80T120L2Q0P2G 功率模块的卓越性能

联合电子推出混动系统动力域多合一控制器PDCU8.1平台
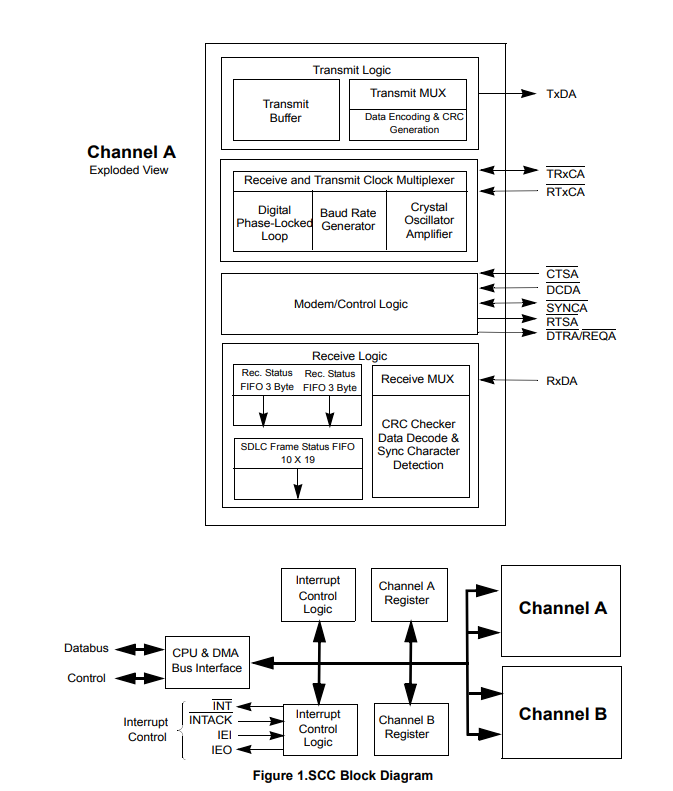
深入剖析Z80C30/Z85C30 CMOS SCC串行通信控制器
谷歌与耶鲁大学合作发布最新C2S-Scale 27B模型
BM2P061MF-Z DC/DC转换器IC文档介绍
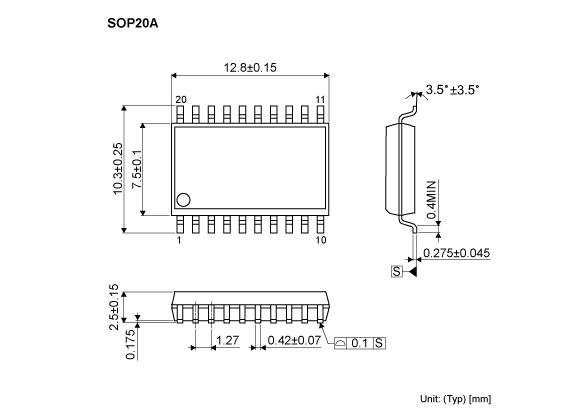
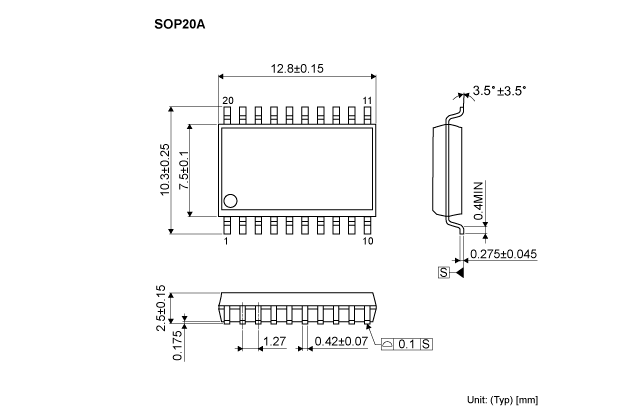
BM2P060MF-Z DC-DC转换器文档介绍
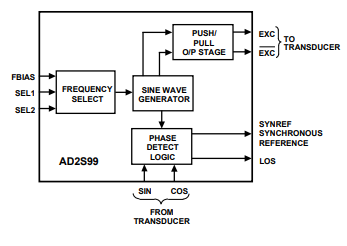
深入了解恩智浦S32E2域控制器

FA20-220S48P2D4 FA20-220S48P2D4

UA10-220S05V3P2D UA10-220S05V3P2D

UA10-220S5V3P2D UA10-220S5V3P2D

DA10-220S3V3P2D4 DA10-220S3V3P2D4

FA20-300S24H2D4P2 FA20-300S24H2D4P2

bq78z100EVM 1s-2s锂离子电池组管理器评估模块






 Compensation Designer 2P2Z 控制器S域模型理解
Compensation Designer 2P2Z 控制器S域模型理解











评论