【SOA用于噪声抑制】非相干光源的强度噪声

----翻译自Anoma Dayawansa McCoy在2005年撰写的博士论文《Intensity Noise Suppression Using A Semiconductor Optical Amplifier: Characterizations and Applications》

概述：

在这一章中讨论了非相干光源中强度噪声的特性，并研究了这种噪声如何受到源强度、光谱形状和带宽等因素的影响，实验结果和数值仿真用于验证和理解这些特性，为后续章节中提出的噪声抑制技术的评估提供了基础。

1 非相干光的统计特性

自发辐射是当今大多数常见光源的基本过程，这类光源（包括自然光源和人造光源）发出的光，是大量受激原子或分子自发跃迁到较低能级时辐射的结果，发射出的光包或光子彼此独立产生，在很宽的光谱范围内随机出现。单个光子的相位是随机的，产生的光是不相干的，通常称为热光。相比之下，激光是高度相干的，由通过受激辐射产生的有序光子组成。

自发辐射本质上是有噪声的，会导致连续光（CW）强度的随机波动。这种强度噪声是由构成光带宽的随机相位光谱分量的拍频引起的，并通过光电检测过程的平方律特性表现出来。从分析角度来看，热光的复电场可以用统计独立的傅里叶分量表示为公式（2.1），其中积分是在光源的整个光带宽Δν上进行计算。

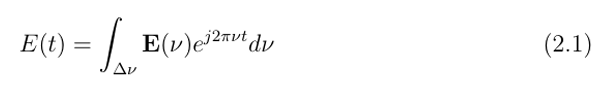
这里，E(ν)=|E| ejΦ是频率ν处的复场分量，|E|和Φ是代表场振荡幅度和相位的随机变量。对于偏振光，|E|)和Φ分别遵循瑞利分布和均匀分布，同时可以证明，在给定的空间和时间点，复场E(t)遵循圆高斯统计[11]。

本论文主要研究窄带偏振非相干光。这种窄带光保留了偏振热光源的统计特性[11,14]，因此可以用公式（2.1）描述，其中Δν现在代表光谱滤波后信号的带宽。

2 测量强度噪声

光信号的强度噪声可以通过探测器光电流的功率谱密度（PSD）来表征。然而，光电流还包括散粒噪声和热噪声分量，为了准确测量光源强度噪声，必须考虑这些分量。

散粒噪声是由光子到达探测器的随机时间引起的，对于PIN光电二极管，散粒噪声PSD，Sshot由公式（2.2）给出：

这里，Ip是平均光电流，它与输入光功率直接相关。q和RL分别是电子电荷和探测器负载电阻。另一方面，热噪声与输入光强度无关，是由负载电阻中电子的随机热运动产生的。其PSD Sthermal可以用公式（2.3）描述，其中kB是玻尔兹曼常数，T是绝对温度。注意，热噪声和散粒噪声的功率谱密度在很宽的频率范围内都是平坦的，因此通常被建模为白噪声过程。

在实际使用非相干光的系统中，热噪声和散粒噪声水平通常远低于光源强度噪声，因此不会显著影响检测到的信号质量。探测器输出的总噪声可以表示为光源、散粒噪声和热噪声的独立贡献之和：

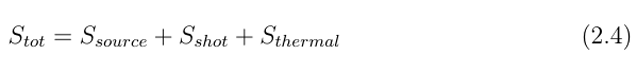
典型光接收器中不同噪声贡献之间的关系将在2.4节中进一步讨论。

除了PSD，噪声还可以用相对强度噪声（RIN）来表征，这是一个直接量化连续波光信号强度噪声水平的品质因数：

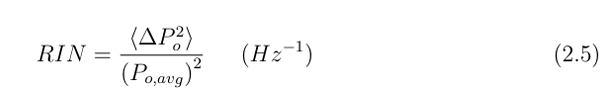
这里ΔPo2是光信号的均方强度波动谱密度（单位为W2/Hz），Po,avg是平均光功率（单位为W）。需要注意的是，ΔPo2是在特定电频率下测量的。由于在接收器中光功率与电流成正比，公式（2.5）也可以用电噪声功率Pe表示为公式（2.6）：

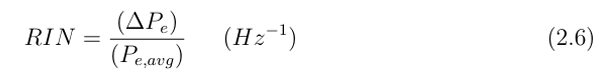
因此，通过测量得到的电噪声PSD，ΔPe与平均电功率Pe,avg的比值，可以得到光信号的RIN。总RIN (RINT) 由公式（2.7）给出，其中f代表感兴趣的频率：

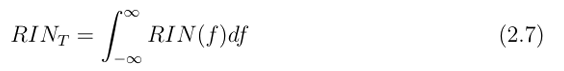
一般来说，RIN可以被视为一种反信噪比（SNR），是评估信号质量的良好品质因数。噪声谱密度给出了系统在感兴趣频率处的总噪声，而RIN是系统性能的度量，因此直接关系到可实现的误码率（BER）。

本文中所有的噪声测量均采用两种方法之一（在进行噪声测量时会指明具体技术），具体取决于所需的电带宽。大多数噪声测量使用低噪声（噪声等效功率为2.5pW/Hz1/2）的New Focus 1811型光接收器，它由一个InGaAs PIN光电二极管和一个跨阻放大器组成。该接收器的3 dB带宽为125 MHz，在1550 nm处其光功率与电流的转换因子约为600A/W。探测器的输出连接到Marconi（型号2382）射频频谱分析仪，用于在所需的100 MHz频率下测量电噪声PSD。在进行RIN测量时，使用数字示波器测量光电探测器输出的平均电压Vavg，并使用P=Vavg2/RL计算电信号的平均功率。测量的不确定度基于频谱分析仪和示波器的额定精度进行估算，计算结果为±1dB。另外，当需要更宽的电带宽时，使用带宽为22GHz的Agilent光波分析仪测量RIN。

3 数值模型

为了更好地理解不同系统参数对光源噪声的影响，开发了一个数值模型来预测窄带非相干光的强度噪声特性。该模型基于H.S. Kim等人在参考文献[14]中提出的数学分析。在该分析中，偏振热光源的强度波动通过关系covI(τ) = |ΓE(τ)|2与光场的统计特性相关联，其中covI(τ)是强度的协方差，ΓE(τ)是输入光场的自相干函数。利用这个关系，结合著名的维纳-辛钦定理，推导出了光源噪声PSD, Ssource(f)的解析表达式，该表达式基于窄带光信号的频谱密度：

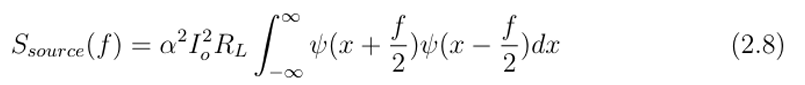
这里，α是光功率到电流的转换因子，Io是光源的强度，RL是光电探测器的负载电阻。Ψ(ν)是光PSD的频谱包络函数，归一化为单位功率并移至中心频率为零。从概念上讲，这个公式表明在特定频率f处的噪声是所有频率差为f的光谱分量对的乘积的叠加。因此，公式（2.8）可用于数值评估任意形状输入光谱下光电探测器输出的强度噪声。数值计算的更多细节在附录A中给出，需要注意的是，模型的输入光PSD可以是解析函数或实验测量的光谱数据。

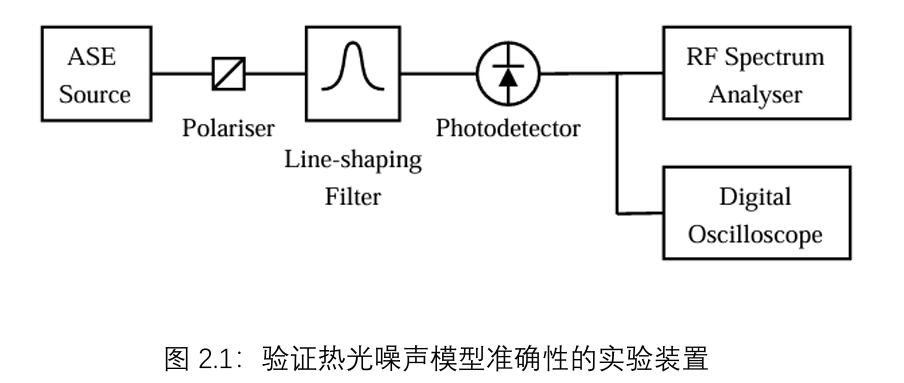
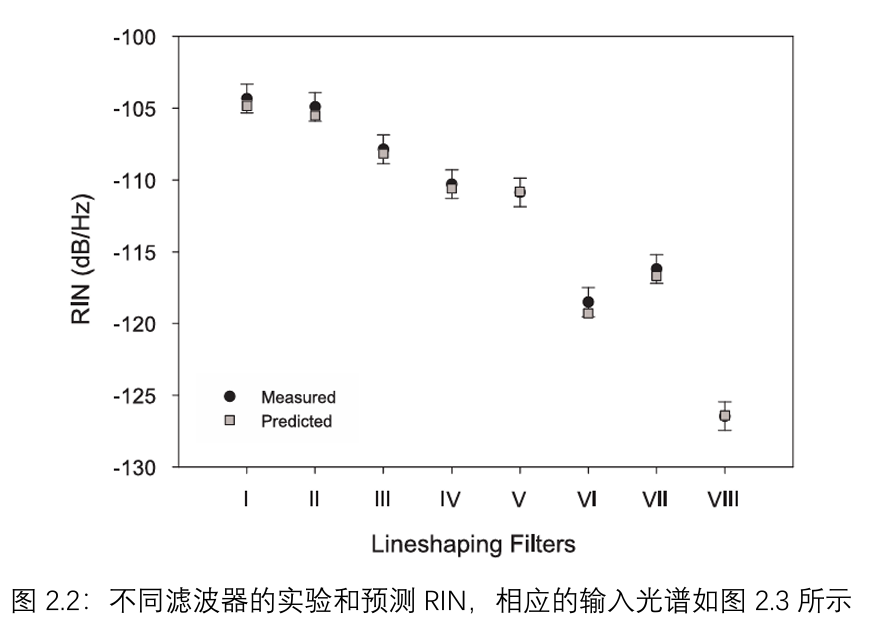
使用图2.1所示的实验装置对数值模型的准确性进行了实验验证。在整个研究过程中，所有实验均使用EDFA产生的ASE作为非相干光源，因为这些光纤光源在我们实验室中很容易获得。所需的窄带输入通过使用无源光滤波器（如FBG）对宽带光谱进行整形得到。本实验中使用的滤波器形状如图2.3所示。使用低噪声光电探测器和频谱分析仪（如2.2节所述）在100 MHz下进行RIN测量，测量结果以及预测的RIN值如图2.2所示。在这种情况下，将实验测量的滤波器函数作为模型的输入。从图2.2中可以明显看出，理论预测与测量结果非常吻合。通过验证数值模型的准确性，我们可以放心地使用它来预测任意光谱形状的偏振热光的RIN。

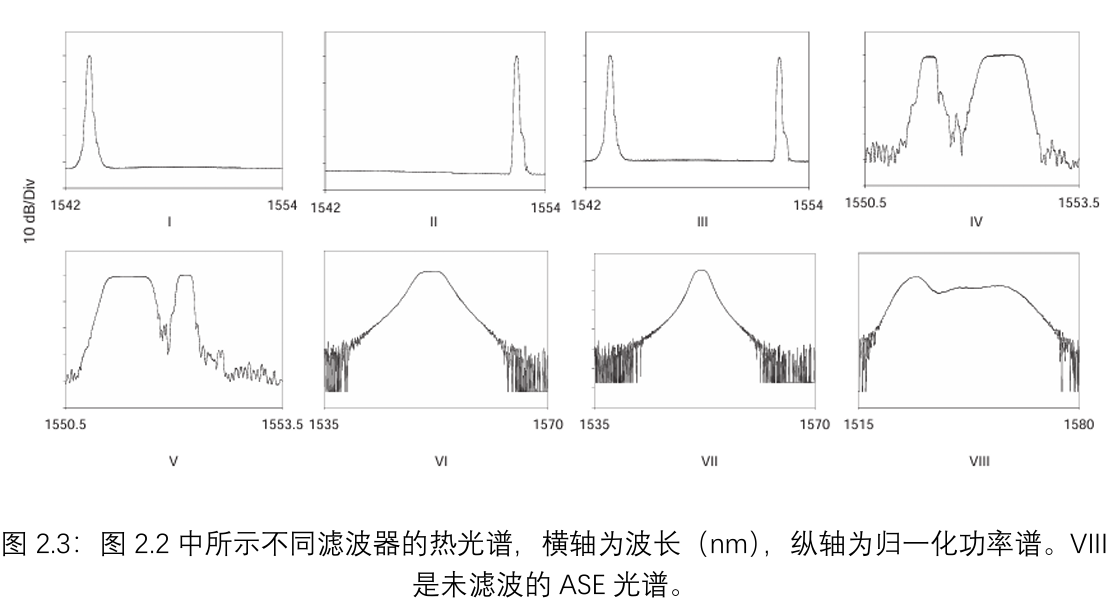
接下来的部分将进一步详细探讨强度噪声的特性。特别是研究RIN与光源强度、带宽、光谱形状、电频率和色散的关系。

4 强度噪声的特性

后续表征所使用的实验装置如图2.4所示。与之前一样，使用EDFA产生的ASE作为非相干宽带光源，5nm带通滤波器和在线EDFA用于增加感兴趣带宽内的光谱密度。在每种情况下，使用前面章节中概述的数值模型估计预测的噪声PSD。

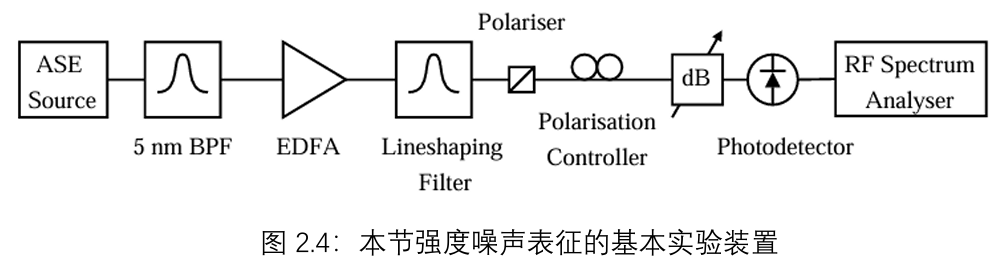
4.1 噪声与光强度的关系

为了研究光源功率对强度噪声的影响，使用可变光衰减器VOA控制进入光接收器的输入功率。在100 MHz的电频率下测量噪声，此特定表征使用的滤波器带宽为0.48 nm（59 GHz）。噪声PSD的实验和预测结果如图2.5所示，同时还给出了散粒噪声和探测器热噪声，散粒噪声Sshot使用公式（2.2）计算，负载电阻为50Ω，探测器底噪是没有光输入时探测器输出的噪声功率, 通过实验测量得到。

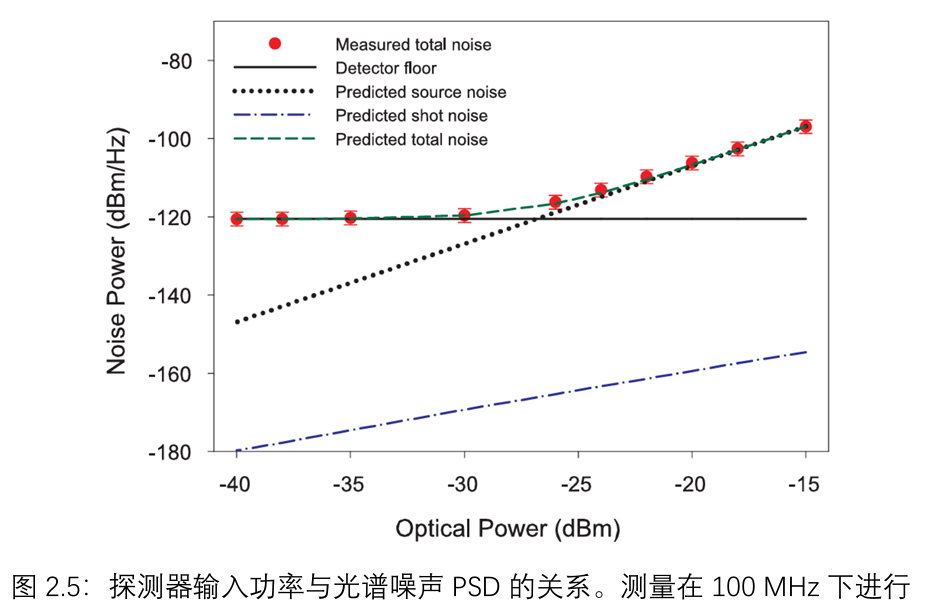
不出所料，预测的总噪声与实验测量结果非常吻合。在较高功率水平下，光源强度噪声占主导，此时光源噪声的预测值也与测量值紧密相符。预测的光源噪声在对数 - 对数尺度上是一条斜率约为2的直线，这与公式（2.8）中光强度与噪声PSD之间的二次关系相对应。在较低功率下，测量值遵循探测器噪声水平，因为在这个区域系统显然受探测器噪声限制。需要注意的是，在本次表征所考虑的功率水平下，散粒噪声的贡献可以忽略不计。

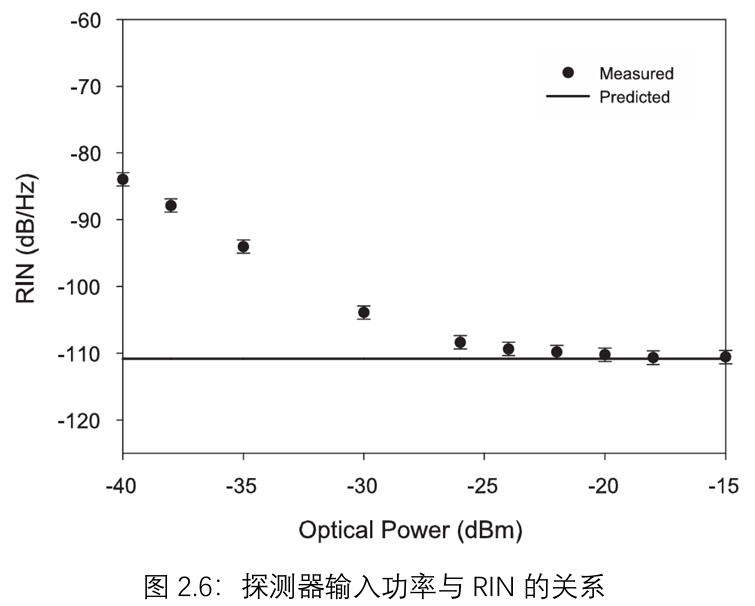
相应的RIN与光强度的关系如图2.6所示。正如公式（2.6）所预期的，预测的RIN与接收光强度无关。然而，在较低功率水平下，实验RIN值与计算值有显著偏差。这种差异是由于探测器噪声限制造成的，在该区域，光功率的降低并不会导致总噪声的可测量降低。另一方面，随着光功率增加，光源噪声也相应增加。一旦光源噪声超过探测器底噪，光强度的任何进一步增加都会导致测量的强度噪声水平成比例增加，从而使RIN保持恒定。这在图2.6中可以明显看出，当功率水平≥-20 dBm时，测量的RIN接近预测值约 -110dB/Hz。在论文的其余部分，所有给出的RIN测量均在光功率为 -14 dBm下进行，此时光源噪声远超过探测器底噪。从上述结果可以明显看出，窄带非相干光的RIN以及因此的SNR不能通过增加接收信号功率来改善。

4.2 噪声与光源带宽的关系

为了量化噪声与光源带宽的关系，对八种不同宽度的滤波器（宽度分别为0.05、0.24、0.5、0.8、1.0、1.3、1.5和2.0 nm）重复进行RIN测量。还为每个滤波器函数计算了相应的RIN值，并与实验数据一起显示在图2.7中。本实验中使用的所有滤波器形状相似，均为具有陡峭滚降的FBG，如插图所示。

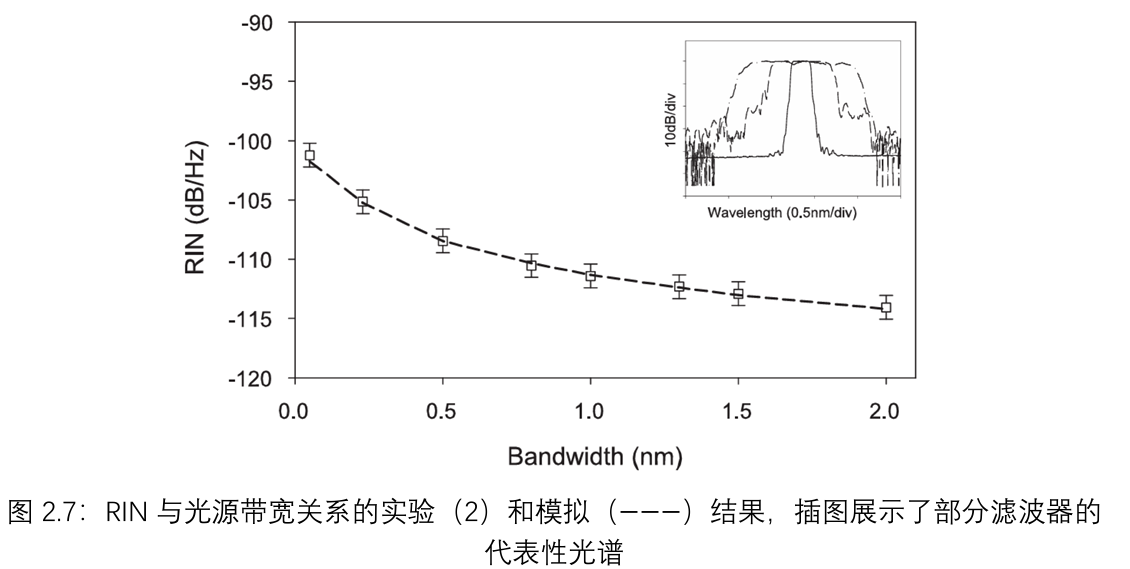
可以看到，RIN随着带宽的增加而降低（即SNR增加）。当线整形滤波器宽度从0.05 nm变化到2.0 nm时，RIN降低了超过12 dB，在线性单位中这是16倍的变化。

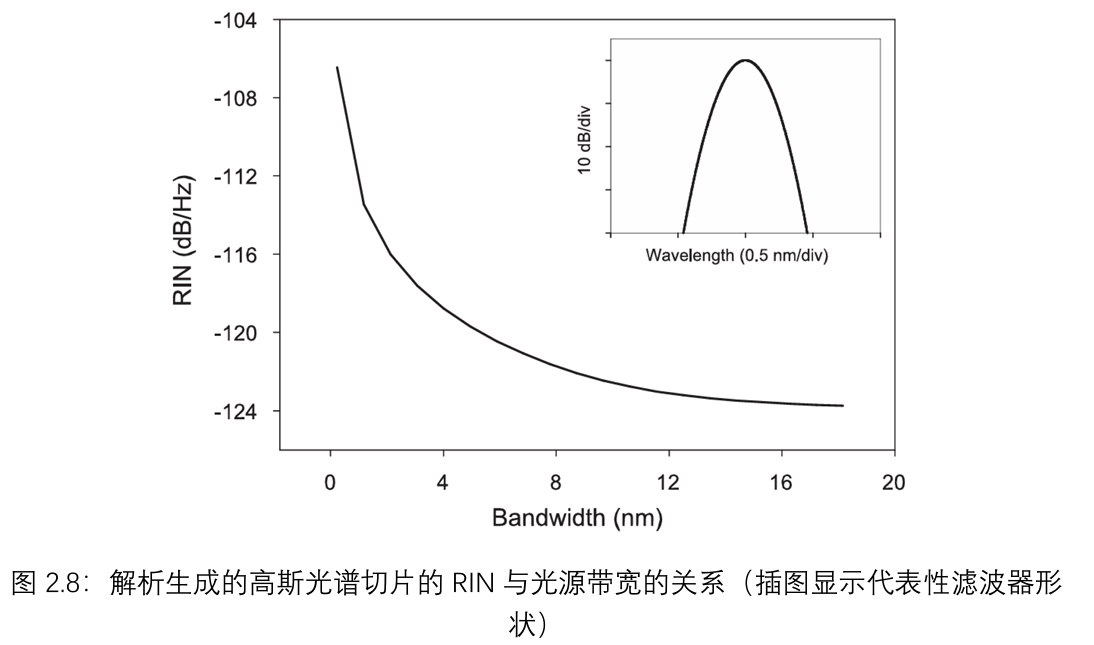
为了在比实验室可用滤波器宽度大得多的范围内评估噪声与光源带宽的关系，使用数值模型计算了不同宽度的解析生成的高斯切片的RIN。结果如图2.8所示，与图2.7呈现相同的趋势，表明RIN与光源带宽成反比。从这些结果可以明显看出，通过增加光源带宽可以显著提高信号质量。

4.3 噪声与光源光谱形状的关系

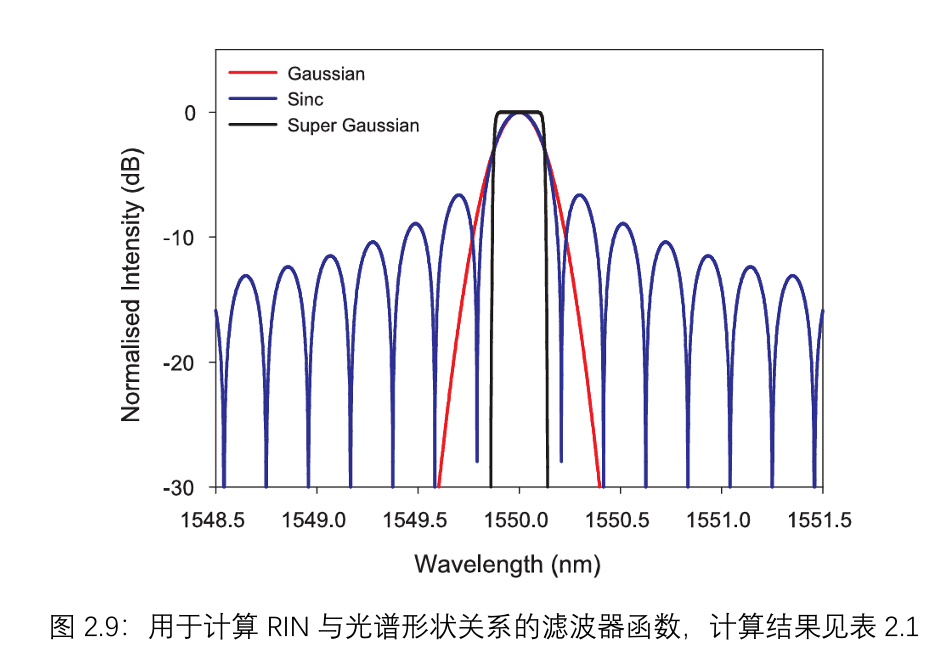
从公式（2.8）明显可知，光源光谱的形状ψ(ν)也会对信号噪声产生影响。因此需要注意，尽管上述图2.7和图2.8呈现出相同的趋势，但由于滤波器形状存在显著差异，实际的相对强度噪声（RIN）值并不能直接进行比较。进一步利用三种解析生成的光谱形状（sinc、高斯和10阶超高斯，如图2.9所示）展开研究，这三种光谱形状具有相同的3 dB带宽。三种光谱对应的计算RIN值如表2.1所示。从这些结果可以看出，尽管3 dB滤波器带宽相同，但不同的光谱形状会导致不同水平的RIN。

这一点也通过实验得到了验证。实验使用了两个3 dB带宽约为0.24 nm的滤波器，其滤波器函数如图2.10所示。陡峭滚降的滤波器（a）的RIN值为-105.2 dB/Hz，而更接近钟形的滤波器（b）的RIN值则明显更优，为-109.1 dB/Hz。

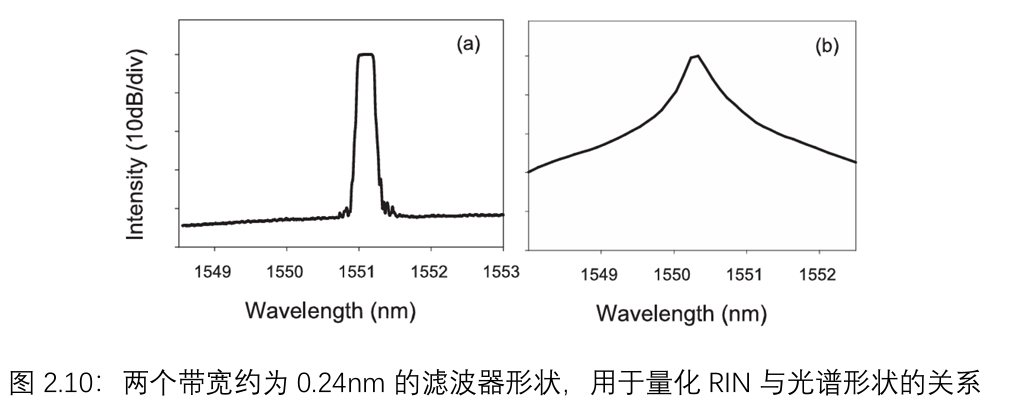
这些结果表明，对于相同的3 dB带宽，具有更陡峭滚降的滤波器比20 dB带宽更宽的同类滤波器显示出明显更高的噪声水平。因此，光源光谱形状在窄带热光的噪声特性中起着重要作用。

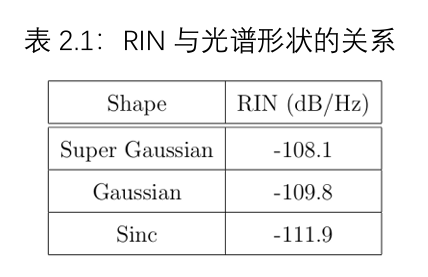
4.4 噪声与电频率的关系

如2.3节之前所讨论的，由公式（2.8）给出的光源噪声Ssource(f)，是所有频率差为f的拍频分量之和。只要f远小于光源带宽Δν ，光源的RIN就可以近似认为与测量频率无关（即白噪声近似是有效的）。然而，当感兴趣的频率接近光带宽时，从公式（2.8）明显可知，频率差为f的拍频分量数量会相应减少，从而降低RIN。从图2.11（a）中可以清楚地看到这一点，图中展示了0.24nm（约30GHz）光源带宽在30GHz频率范围内的RIN计算结果；在约5GHz之后，RIN出现明显的“滚降”。

在实验中，只要光源带宽Δν远大于探测器带宽，白噪声近似就成立。通过测量30GHz光源切片在22GHz带宽上的RIN光谱也证实了这一点。同样，RIN在5GHz的光谱范围内大致保持恒定，之后才观察到轻微的滚降。

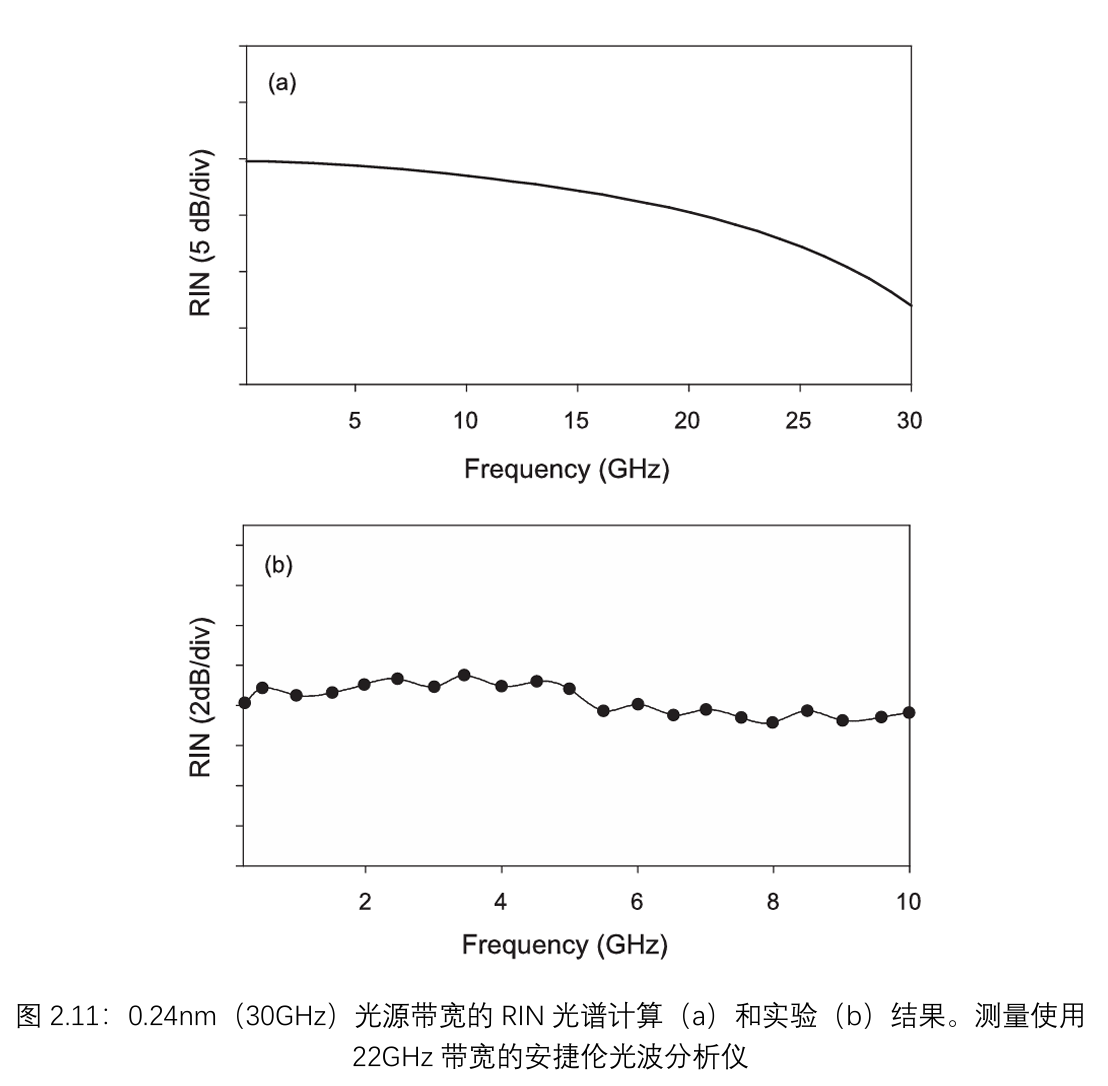
4.5 噪声与色散的关系

如2.1节所讨论的，由于各个相位分量的统计独立性，不同光谱分量之间的相对相位延迟不会改变热光场的统计特性，通过对光施加色散进行实验验证了这一点。

我们将窄带热光（光谱带宽为0.24nm）注入到不同长度的单模光纤（SMF）中，然后监测输出的RIN。在100MHz下测量的RIN如图2.12所示，正如预期的那样，RIN确实不随增加的色散而变化。相比之下，引入饱和SOA来抑制热光的强度波动，会产生统计特性截然不同的光，其噪声特性实际上会受到色散的影响。这将在第3章中进行更详细的讨论。

5 总结与讨论

通过实验和理论研究了窄带热光中强度噪声的特性。证实了过量光子噪声与光强度成正比，因此，不能通过增加信号功率来提高信噪比。噪声还被证明与光源带宽成反比，并且强烈依赖于光谱分布的形状。热光的白噪声近似在很宽的电带宽范围内是有效的。最后，正如预期的那样，由于非相干光的随机相对相位关系，测量到的噪声不受色散的影响。

注：本文由天津见合八方光电科技有限公司挑选并翻译，旨在推广和分享相关半导体光放大器SOA基础知识，助力SOA技术的发展和应用。特此告知，本文系经过人工翻译而成，虽本公司尽最大努力保证翻译准确性，但不排除存在误差、遗漏或语义解读导致的不完全准确性，建议读者阅读原文或对照阅读，也欢迎指出错误，共同进步。

审核编辑 黄宇