笔记1中我们利用 numpy 搭建了神经网络最简单的结构单元:感知机。笔记2将继续学习如何手动搭建神经网络。我们将学习如何利用 numpy 搭建一个含单隐层的神经网络。单隐层顾名思义,即仅含一个隐藏层的神经网络,抑或是成为两层网络。
继续回顾一下搭建一个神经网络的基本思路和步骤:
定义网络结构(指定输出层、隐藏层、输出层的大小)
初始化模型参数
循环操作:执行前向传播/计算损失/执行后向传播/权值更新
定义网络结构
假设 X 为神经网络的输入特征矩阵,y 为标签向量。则含单隐层的神经网络的结构如下所示:
网络结构的函数定义如下:
deflayer_sizes(X,Y): n_x=X.shape[0]#sizeofinputlayer n_h=4#sizeofhiddenlayer n_y=Y.shape[0]#sizeofoutputlayer return(n_x,n_h,n_y)
其中输入层和输出层的大小分别与 X 和 y 的 shape 有关。而隐层的大小可由我们手动指定。这里我们指定隐层的大小为4。
初始化模型参数
假设 W1 为输入层到隐层的权重数组、b1 为输入层到隐层的偏置数组;W2 为隐层到输出层的权重数组,b2 为隐层到输出层的偏置数组。于是我们定义参数初始化函数如下:
def initialize_parameters(n_x, n_h, n_y):
W1 = np.random.randn(n_h, n_x)*0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h)*0.01
b2 = np.zeros((n_y, 1))
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters其中对权值的初始化我们利用了 numpy 中的生成随机数的模块 np.random.randn ,偏置的初始化则使用了 np.zero 模块。通过设置一个字典进行封装并返回包含初始化参数之后的结果。
前向传播
在定义好网络结构并初始化参数完成之后,就要开始执行神经网络的训练过程了。而训练的第一步则是执行前向传播计算。假设隐层的激活函数为
tanh 函数,
输出层的激活函数为 sigmoid 函数。则前向传播计算表示为:
定义前向传播计算函数为:
def forward_propagation(X, parameters): # Retrieve each parameter from the dictionary "parameters"
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
# Implement Forward Propagation to calculate A2 (probabilities)
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, Z1) + b2
A2 = sigmoid(Z2)
assert(A2.shape == (1, X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache从参数初始化结果字典里取到各自的参数,然后执行一次前向传播计算,将前向传播计算的结果保存到 cache 这个字典中, 其中 A2 为经过 sigmoid 激活函数激活后的输出层的结果。
计算当前训练损失
前向传播计算完成后我们需要确定以当前参数执行计算后的的输出与标签值之间的损失大小。与笔记1一样,损失函数同样选择为交叉熵损失:
定义计算损失函数为:
def compute_cost(A2, Y, parameters):
m = Y.shape[1] # number of example
# Compute the cross-entropy cost
logprobs = np.multiply(np.log(A2),Y) + np.multiply(np.log(1-A2), 1-Y)
cost = -1/m * np.sum(logprobs)
cost = np.squeeze(cost) # makes sure cost is the dimension we expect.
assert(isinstance(cost, float))
return cost执行反向传播
当前向传播和当前损失确定之后,就需要继续执行反向传播过程来调整权值了。中间涉及到各个参数的梯度计算,具体如下图所示:
根据上述梯度计算公式定义反向传播函数:
def backward_propagation(parameters, cache, X, Y):
m = X.shape[1]
# First, retrieve W1 and W2 from the dictionary "parameters".
W1 = parameters['W1']
W2 = parameters['W2']
# Retrieve also A1 and A2 from dictionary "cache".
A1 = cache['A1']
A2 = cache['A2']
# Backward propagation: calculate dW1, db1, dW2, db2.
dZ2 = A2-Y
dW2 = 1/m * np.dot(dZ2, A1.T)
db2 = 1/m * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.dot(W2.T, dZ2)*(1-np.power(A1, 2))
dW1 = 1/m * np.dot(dZ1, X.T)
db1 = 1/m * np.sum(dZ1, axis=1, keepdims=True)
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads将各参数的求导计算结果放入字典 grad 进行返回。
这里需要提一下的是涉及到的关于数值优化方面的知识。在机器学习中,当所学问题有了具体的形式之后,机器学习就会形式化为一个求优化的问题。不论是梯度下降法、随机梯度下降、牛顿法、拟牛顿法,抑或是
Adam 之类的高级的优化算法,这些都需要花时间掌握去掌握其数学原理。
权值更新
迭代计算的最后一步就是根据反向传播的结果来更新权值了,更新公式如下:
由该公式可以定义权值更新函数为:
def update_parameters(parameters, grads, learning_rate = 1.2): # Retrieve each parameter from the dictionary "parameters"
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
# Retrieve each gradient from the dictionary "grads"
dW1 = grads['dW1']
db1 = grads['db1']
dW2 = grads['dW2']
db2 = grads['db2']
# Update rule for each parameter
W1 -= dW1 * learning_rate
b1 -= db1 * learning_rate
W2 -= dW2 * learning_rate
b2 -= db2 * learning_rate
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters这样,前向传播-计算损失-反向传播-权值更新的神经网络训练过程就算部署完成了。当前了,跟笔记1一样,为了更加 pythonic 一点,我们也将各个模块组合起来,定义一个神经网络模型:
def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
# Initialize parameters, then retrieve W1, b1, W2, b2. Inputs: "n_x, n_h, n_y". Outputs = "W1, b1, W2, b2, parameters".
parameters = initialize_parameters(n_x, n_h, n_y)
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
A2, cache = forward_propagation(X, parameters)
# Cost function. Inputs: "A2, Y, parameters". Outputs: "cost".
cost = compute_cost(A2, Y, parameters)
# Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
grads = backward_propagation(parameters, cache, X, Y)
# Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
parameters = update_parameters(parameters, grads, learning_rate=1.2)
# Print the cost every 1000 iterations
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
return parameters以上便是本节的主要内容,利用 numpy 手动搭建一个含单隐层的神经网路。从零开始写起,打牢基础,待到结构熟练,原理吃透,再去接触一些主流的深度学习框架才是学习深度学习的最佳途径。
本文来自《自兴动脑人工智能》项目部:凯文。
-
神经网络
+关注
关注
42文章
4829浏览量
106887 -
AI
+关注
关注
90文章
38303浏览量
297375 -
人工智能
+关注
关注
1813文章
49785浏览量
261915
发布评论请先 登录
NMSIS神经网络库使用介绍
在Ubuntu20.04系统中训练神经网络模型的一些经验
CICC2033神经网络部署相关操作
液态神经网络(LNN):时间连续性与动态适应性的神经网络






 【连载】深度学习笔记2:手写一个单隐层的神经网络
【连载】深度学习笔记2:手写一个单隐层的神经网络

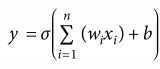










评论