什么是振动？几个振动的例子

什么是振动？简单的说，就是某个物理量的值随时间周期变化的现象。

振动的物理量随时间周期变化的曲线叫振动曲线，例如（仔细看，周期是存在的哦）

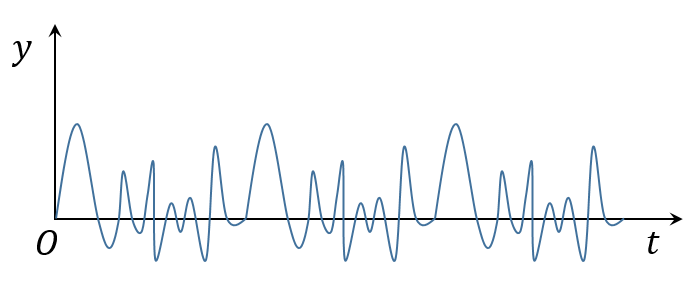
最常见的振动是机械振动，随时间周期变化的那个物理量是位置。质点的位置是一个时间的函数，对于一般的运动来说，它就是一个矢量函数，即

它也被称作运动方程。对于机械振动来说，由于位置是周期性变化的，运动方程应该是一个时间的周期函数。

机械振动非常直观，但它并非振动的全部，广义的振动可以是任何物理量随时间的周期变化。

例如，一天中，早上温度最低，随着太阳升起，温度逐渐上升，到下午2点左右，温度达到最高，然后开始降低，直到第二天早上达到最低，如此反复。

更简单的例子，摆动的吊灯，相对于竖直线的偏离角度，随时间来回往复的变化。类似的，一个持续摆动的牛顿摆也是如此。

01

几个振动的例子

下面来仔细看几个振动的例子。

一个球竖直上抛后落下，与地面弹性碰撞后弹起，再落下又弹起，这个过程就是一个典型的振动过程。以上抛点为原点，向上为轴，则其振动曲线如下，它由一段段完全相同的抛物线拼接而成。

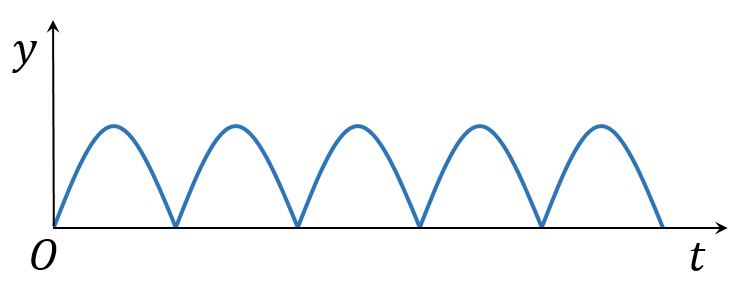
温馨提示：由于实际的机械振动曲线中，不可能出现速度不存在的点——例如图中那些导数不存在的地方。所以，这里列举的几个振动只是理论上的振动曲线，作为机械振动是不可能真实存在的。

设上图中每一段抛物线的宽度为，高为。你能写出描述该振动的函数吗？看起来很难，因为它不是一个普通的周期函数，不信你可以试试。

太复杂？那就来个更简单点的吧，看下面的振动曲线，某个物理量随时间变化如下

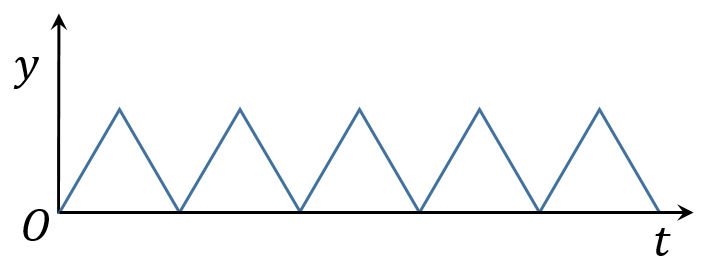
曲线中的三角形都是全等正三角形，边长为。是不是仍然无法写出它的函数？

的确，除非你借助那些特殊的函数，例如对内的部分，可表示为

温馨提示：这里面的和围起来是floor函数的符号，它是用来取整的。

否则，你还真没办法写出它的表达式。

再看一种更简单的振动曲线，某物理量随时间变化如下

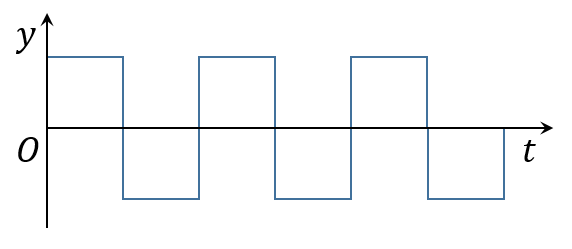
设曲线的每一段长度都为。你能写出这个函数吗？

再次抱歉，你同样写不出来！除非你借助符号函数将其写成

温馨提示：的定义为：称作符号函数。

看到了吧，那些看起来很直观的振动，其运动方程却都如此复杂！

看来，从数学上讲，这几个振动都不太好对付啊。

那么，有没有简单一点的振动呢？

02

匀速圆周运动与简谐振动

仔细想一下，什么样的振动可能是最简单的振动呢？

别忘了，振动的一般定义是物理量随时间周期变化的运动，不要总想着沿一个维度左右、上下来回的运动，思路放开一点嘛！

绕着一个闭合路径做周期运动算不算振动？当然算！

矮油！这么一提示，顿时就想到了，它不就是匀速圆周运动嘛！

没错，我相信大多数人认为非它莫属！是啊，还有什么周期运动有匀速圆周运动这般简单和谐？！

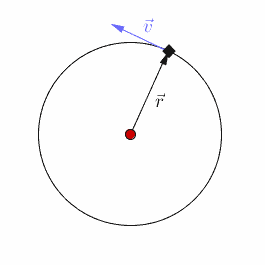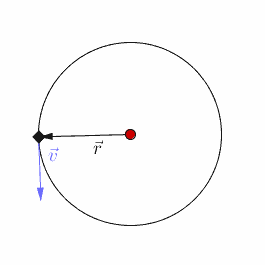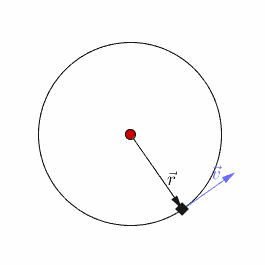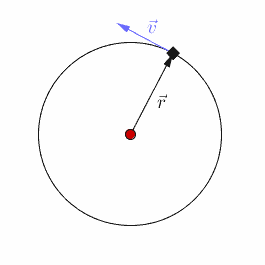
设匀速圆周运动的角速度为，则每隔的时间，质点重回原位。运动具有周期性，所以圆周运动的确是振动！一种极为特殊的振动！

既然匀速圆周运动如此简单，那么它的运动方程是什么呢？

设其圆周的半径为，角速度为，设零时刻，它相对轴的正向已转过了角，则运动方程为：

搞半天，就只有匀速圆周运动能用一个比较简单的周期函数表示。

那么，匀速圆周运动的振动方程意味着什么呢？

看看它所包含的东东——正弦和余弦函数！

物理上定义，位置随时间按照正弦或余弦函数变化的振动叫做简谐振动。其运动方程可表示为或例如弹簧振子的振动和单摆的小角度摆动都呈现这种形式。

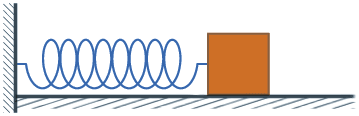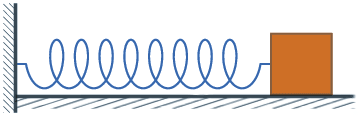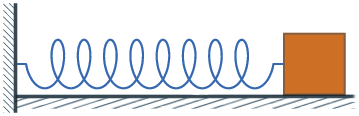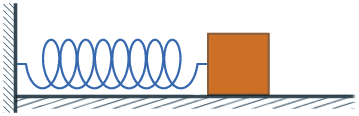
没错，匀速圆周运动本身就是由两个垂直的简谐振动合成得到的，正因为它的两个分振动分别由正弦和余弦函数描述，所以匀速圆周运动也是周期运动！

现在你知道了，匀速圆周运动不是最简单的振动！因为它包含两个更基本的振动。

如下图所示，可以看到，匀速圆周运动沿着圆的任一条直径上的分运动就是一个简谐振动。

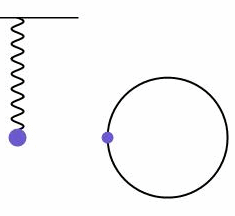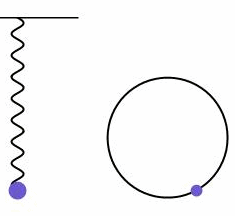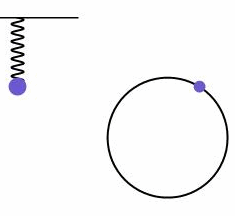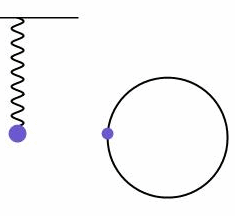
受此启发，设一个长度固定的矢量绕起点以角速度沿逆时针匀速转动，它的箭头在某条直径上的投影的运动是一个简谐振动。换句话说，任何一个简谐振动的背后总对应着一个旋转矢量，如下图

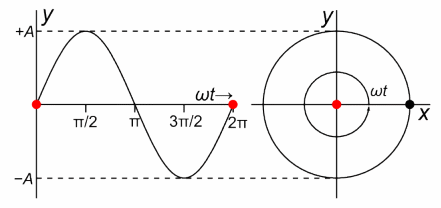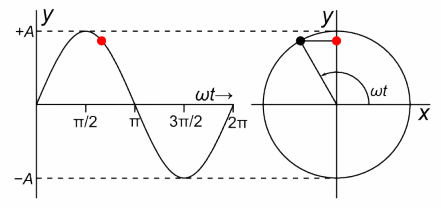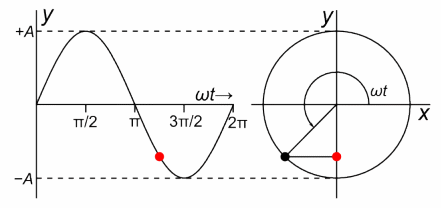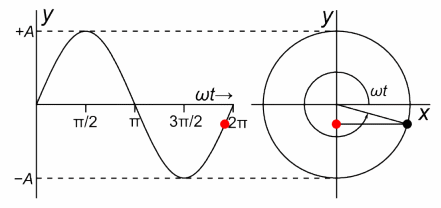
但实际上，简谐振动才是构成匀速圆周运动的基本元素，而不是相反。只不过对大多数人来说，匀速圆周运动更易于理解，所以借助“旋转矢量”，简谐振动看起来更直观。

03

正弦和余弦：最基本的周期函数

如此看来，只要用数学中的周期函数，或周期函数的组合，来构建运动方程，那么不就可以得到各种各样的振动吗？

那么，除了正弦和余弦，还有哪些周期函数呢？

周期函数，这么重要的一类函数，应该很多吧？

赶紧翻数学手册！

然而，结果有点令人意外！

除了正弦和余弦函数之外，要不就是一些由它俩构造的周期函数，比如tan、ctan和sec等等；要不就是一些不光滑的周期函数——就像我前面列举的三角和方形函数，它们根本无法代表真实的运动。

换句话说，正弦和余弦函数就是唯二的俩周期函数！

难怪啊难怪，难怪一般的周期运动都如此复杂，因为根本不存在简单的周期函数能够描述它们；难怪匀速圆周运动如此简单！原来是因为它所包含的两个振动成分是如此纯粹！

呃，这个发现简直太厉害了！

到此，你可能隐隐的感觉到：或许一切周期函数之所以能成为周期函数，本质上都归结于正弦和余弦函数？

事实的确如此！周期函数之所以是周期函数，一切皆因正弦和余弦函数这对孪生兄弟！谁叫他俩是仅有的两个“原创型”的光滑周期函数呢？

数学上可以证明，一个周期函数总可以通过若干个正弦和余弦函数组合来得到，即这就是傅里叶级数，其中系数(含)和为

举个例子，下面这个函数的图像看起来很复杂吧？

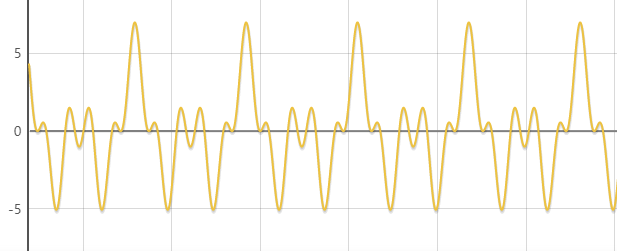
但实际上，此函数由三个余弦函数加起来得到，具体表达式是：你可用Matlab或者随便一个在线绘图工具来验证一下。

讲到这里意识到，之所以任意周期函数都能用正弦和余弦函数的组合来表示，这不是因为他哥俩多厉害，纯粹是因为物以稀为贵——只有他俩是最简单的周期函数。

换句话说，只有他俩才拥有周期的创始基因，但凡其他周期函数者，皆因他俩而起也，皆继承于他俩，由他俩组合而得。

04

简谐振动：最简单的振动

既然一般的周期函数可看作由正弦和余弦函数组合而成，那么相应的，任何一个一般的振动总可以看作是若干个正弦和余弦函数所表示的振动的合成。

不错，正弦和余弦函数是周期函数的基本元素，它们所描述的振动是最基本、最简单的振动！

例如，除匀速圆周运动之外，周期的椭圆运动也是由相互垂直的两个简谐振动合成得到。

而任意周期运动，总可由若干个简谐振动合成得到。例如，下面这种振动（蓝色线）可看作是由多个频率不同的简谐振动合成的，所采用的简谐振动越多，合成的振动越接近蓝色线代表的振动。

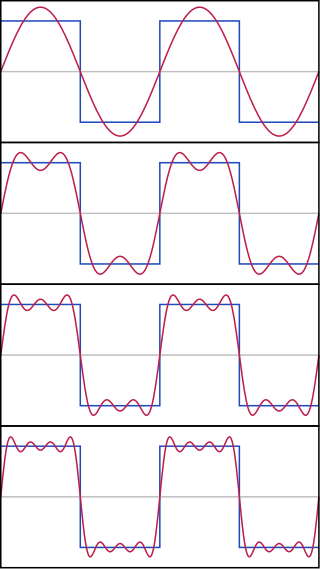
所以，正弦或余弦函数所描述的振动可看作是振动的基本成分。之所以被称作简谐振动，“简”字正是强调它是自然界中最简单的振动。而“谐”字的意思是，振动一直持续下去，强调其能量不会耗散。

更广泛的，非周期的函数可以看作是周期无限大的函数，它们也可以看作是正弦和余弦通过加权函数的组合，这就是傅里叶变换，它是傅里叶级数的推广。据此，即使非周期运动，形式上也可看作是由简谐振动合成的。

因此，正弦和余弦函数也可看作构成一切函数的基本元素，由他们描述的振动——简谐振动，是构成一切运动的基本单元。

审核编辑 ：李倩