简述FPGA的快速傅立叶变换

摘要：在对FFT（快速傅立叶变换）算法进行研究的基础上，描述了用FPGA实现FFT的方法，并对其中的整体结构、蝶形单元及性能等进行了分析。 傅立叶变换是数字信号处理中的基本操作，广泛应用于表述及分析离散时域信号领域。但由于其运算量与变换点数Ｎ的平方成正比关系，因此，在Ｎ较大时，直接应用ＤＦＴ算法进行谱变换是不切合实际的。然而，快速傅立叶变换技术的出现使情况发生了根本性的变化。本文主要描述了采用ＦＰＧＡ来实现２ｋ／４ｋ／８ｋ点ＦＦＴ的设计方法。

１整体结构

一般情况下，Ｎ点的傅立叶变换对为： 其中，ＷＮ＝ｅｘｐ（－２ ｐｉ／Ｎ）。Ｘ（ｋ）和ｘ（ｎ）都为复数。与之相对的快速傅立叶变换有很多种，如ＤＩＴ（时域抽取法）、ＤＩＦ（频域抽取法）、Ｃｏｏｌｅｙ－Ｔｕｋｅｙ和Ｗｉｎｏｇｒａｄ等。对于２ｎ傅立叶变换，Ｃｏｏｌｅｙ－Ｔｕｋｅｙ算法可导出ＤＩＴ和ＤＩＦ算法。

本文运用的基本思想是Ｃｏｏｌｅｙ－Ｔｕｋｅｙ算法，即将高点数的傅立叶变换通过多重低点数傅立叶变换来实现。虽然ＤＩＴ与ＤＩＦ有差别，但由于它们在本质上都是一种基于标号分解的算法，故在运算量和算法复杂性等方面完全一样，而没有性能上的优劣之分，所以可以根据需要任取其中一种，本文主要以ＤＩＴ方法为对象来讨论。

Ｎ＝８１９２点ＤＦＴ的运算表达式为： 式中，ｍ＝（４ｎ１＋ｎ２）（２０４８ｋ１＋ｋ２）（ｎ＝４ｎ１＋ｎ２，ｋ＝２０４８ｋ１＋ｋ２）其中ｎ１和ｋ２可取０，１，．．．，２０４７，ｋ１和ｎ２可取０，１，２，３。 由式（３）可知，８ｋ傅立叶变换可由４×２ｋ的傅立叶变换构成。

同理，４ｋ傅立叶变换可由２×２ｋ的傅立叶变换构成。而２ｋ傅立叶变换可由１２８×１６的傅立叶变换构成。１２８的傅立叶变换可进一步由１６×８的傅立叶变换构成，归根结底，整个傅立叶变换可由基２、基４的傅立叶变换构成。２ｋ的ＦＦＴ可以通过５个基４和１个基２变换来实现；

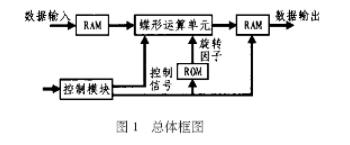
４ｋ的ＦＦＴ变换可通过６个基４变换来实现；８ｋ的ＦＦＴ可以通过６个基４和１个基２变换来实现。也就是说：ＦＦＴ的基本结构可由基２／４模块、复数乘法器、存储单元和存储器控制模块构成，其整体结构如图１所示。 图１中，ＲＡＭ用来存储输入数据、运算过程中的中间结果以及运算完成后的数据，ＲＯＭ用来存储旋转因子表。蝶形运算单元即为基２／４模块，控制模块可用于产生控制时序及地址信号，以控制中间运算过程及最后输出结果。

２蝶形运算器的实现

基４和基２的信号流如图２所示。

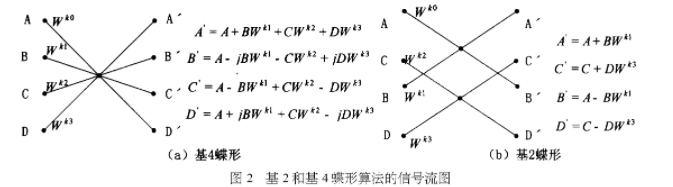
图中，若Ａ＝ｒ０＋ｊ＊ｉ０，Ｂ＝ｒ１＋ｊ＊ｉ１，Ｃ＝ｒ２＋ｊ＊ｉ２，Ｄ＝ｒ３＋ｊ＊ｉ３是要进行变换的信号，Ｗｋ０＝ｃ０＋ｊ＊ｓ０＝１，Ｗｋ１＝ｃ１＋ｊ＊ｓ１，Ｗｋ２＝ｃ２＋ｊ＊ｓ２，Ｗｋ３＝ｃ３＋ｊ＊ｓ３为旋转因子，将其分别代入图２中的基４蝶形运算单元，

则有： Ａ′＝［ｒ０＋（ｒ１×ｃ１－ｉ１×ｓ１）＋（ｒ２×ｃ２－ｉ２×ｓ２）＋（ｒ３×ｃ３－ｉ３×ｓ３）］＋ｊ［ｉ０＋（ｉ１×ｃ１＋ｒ１×ｓ１）＋（ｉ２×ｃ２＋ｒ２×ｓ２）＋（ｉ３×ｃ３＋ｒ３×ｓ３）］？？ （４） Ｂ′＝［ｒ０＋（ｉ１×ｃ１＋ｒ１×ｓ１）－（ｒ２×ｃ２－ｉ２×ｓ２）－（ｉ３×ｃ３＋ｒ３×ｓ３）］＋ｊ［ｉ０－（ｒ１×ｃ１－ｉ１×ｓ１）－（ｉ２×ｃ２＋ｒ２×ｓ２）＋（ｒ３×ｃ３－ｉ３×ｓ３）］ （５） Ｃ′＝［ｒ０－（ｒ１×ｃ１－ｉ１×ｓ１）＋（ｒ２×ｃ２－ｉ２×ｓ２）－（ｒ３×ｃ３－ｉ３×ｓ３）］＋ｊ［ｉ０－（ｉ１×ｃ１＋ｒ１×ｓ１）＋（ｉ２×ｃ２＋ｒ２×ｓ２）－（ｉ３×ｃ３＋ｒ３×ｓ３）］ （６） Ｄ′＝［ｒ０－（ｉ１×ｃ１＋ｒ１×ｓ１）－（ｒ２×ｃ２－ｉ２×ｓ２）＋（ｉ３×ｃ３＋ｒ３×ｓ３）］＋ｊ［ｉ０＋（ｒ１×ｃ１－ｉ１×ｓ１）－（ｉ２×ｃ２＋ｒ２×ｓ２）－（ｒ３×ｃ３－ｉ３×ｓ３）］？？ （７）

而在基２蝶形中，Ｗｋ０和Ｗｋ２的值均为１，这样，将Ａ，Ｂ，Ｃ和Ｄ的表达式代入图２中的基２运算的四个等式中，则有： Ａ′＝ｒ０＋（ｒ１×ｃ１－ｉ１×ｓ１）＋ｊ［ｉ０＋（ｉ１×ｃ１＋ｒ１×ｓ１）］？？ （８） Ｂ′＝ｒ０－ （ｒ１×ｃ１－ｉ１×ｓ１）＋ｊ［ｉ０－（ｉ１×ｃ１＋ｒ１×ｓ１）］ （９） Ｃ′＝ｒ２＋（ｒ３×ｃ３－ｉ３×ｓ３）＋ｊ［ｉ０＋（ｉ３×ｃ３＋ｒ３×ｓ３）］？？ （１０） Ｄ′＝ｒ２－（ｒ３×ｃ３－ｉ３×ｓ３）＋ｊ［ｉ０－（ｉ３×ｃ３＋ｒ３×ｓ３）］？？ （１１） 在上述式（４）～（１１）中有很多类同项，如ｉ１×ｃ１＋ｒ１×ｓ１和ｒ１×ｃ１－ｉ１×ｓ１等，

它们仅仅是加减号的不同，其结构和运算均类似，这就为简化电路提供了可能。同时，在蝶形运算中，复数乘法可以由实数乘法以一定的格式来表示，这也为设计复数乘法器提供了一种实现的途径。 以基４为例，在其运算单元中，实际上只需做三个复数乘法运算，即只须计算ＢＷｋ１、ＣＷｋ２和ＤＷｋ３的值即可。

这样在一个基４蝶形单元里面，最多只需要３个复数乘法器就可以了。在实际过程中，在不提高时钟频率下，只要将时序控制好？煴憧衫？用流水线（Ｐｉｐｅｌｉｎｅ）技术并只用一个复数乘法器就可完成这三个复数乘法，大大节省了硬件资源。

３ＦＦＴ的地址

ＦＦＴ变换后输出的结果通常为一特定的倒序，因此，几级变换后对地址的控制必须准确无误。 倒序的规律是和分解的方式密切相关的，以基８为例，其基本倒序规则如下： 基８可以用２×２×２**基２变换来表示，则其输入顺序则可用二进制序列（ｎ１ ｎ２ ｎ３）来表示，变换结束后，其顺序将变为（ｎ３ ｎ２ ｎ１）。

如：Ｘ？煟埃保保？→ ｘ？煟保保埃牐？即输入顺序为３，输出时顺序变为６。 更进一步，对于基１６的变换，可由２×２×２×２，４×４，４×２×２等形式来构成，相对于不同的分解形式，往往会有不同的倒序方式。以４×４为例，其输入顺序可以用二进制序列（ｎ１ ｎ２ ｎ３ ｎ４）来表示变换结束后，其顺序可变为（（ｎ３ ｎ４）（ｎ１ ｎ２））。

如：Ｘ？煟埃保保保？→ ｘ？煟保保埃保牎＜词淙胨承蛭？７，输出时顺序变为１３。 在２ｋ／４ｋ／８ｋ的傅立叶变换中，由于要经过多次的基４和基２运算，因此，从每次运算完成后到进入下一次运算前，应对运算的结果进行倒序，以保证运算的正确性。

４旋转因子

Ｎ点傅立叶变换的旋转因子有着明显的周期性和对称性。其周期性表现为： FFT之所以可使运算效率得到提高，就是利用 ＦＦＴ之所以可使运算效率得到提高，就是利用了对称性和周期性把长序列的ＤＦＴ逐级分解成几个序列的ＤＦＴ，并最终以短点数变换来实现长点数变换。

根据旋转因子的对称性和周期性，在利用ＲＯＭ存储旋转因子时，可以只存储旋转因子表的一部分，而在读出时增加读出地址及符号的控制，这样可以正确实现ＦＦＴ。因此，充分利用旋转因子的性质，可节省７０％以上存储单元。 实际上，由于旋转因子可分解为正、余弦函数的组合，故ＲＯＭ中存的值为正、余弦函数值的组合。

对２ｋ／４ｋ／８ｋ的傅立叶变换来说，只是对一个周期进行不同的分割。由于８ｋ变换的旋转因子包括了２ｋ／４ｋ的所有因子，因此，实现时只要对读ＲＯＭ的地址进行控制，即可实现２ｋ／４ｋ／８ｋ变换的通用。

５存储器的控制

因ＦＦＴ是为时序电路而设计的，因此，控制信号要包括时序的控制信号及存储器的读写地址，并产生各种辅助的指示信号。同时在计算模块的内部，为保证高速，所有的乘法器都须始终保持较高的利用率。这意味着在每一个时钟来临时都要向这些单元输入新的操作数，而这一切都需要控制信号的紧密配合。

为了实现ＦＦＴ的流形运算，在运算的同时，存储器也要接收数据。这可以采用乒乓ＲＡＭ的方法来完成。

这种方式决定了实现ＦＦＴ运算的最大时间。对于４ｋ操作，其接收时间为４０９６个数据周期，这样？煟疲疲缘淖畲笤怂闶奔渚褪牵矗埃梗陡鍪？据周期。另外，由于输入数据是以一定的时钟为周期依次输入的，故在进行内部运算时，可以用较高的内部时钟进行运算，然后再存入ＲＡＭ依次输出。

为节省资源，可对存储数据ＲＡＭ采用原址读出原址写入的方法，即在进行下一级变换的同时，首先应将结果回写到读出数据的ＲＡＭ存贮器中；而对于ＲＯＭ，则应采用与运算的数据相对应的方法来读出存储器中旋转因子的值。

在２ｋ／４ｋ／８ｋ傅立叶变换中，要实现通用性，控制器是最主要的模块。２ｋ、４ｋ、８ｋ变换具有不同的内部运算时间和存储器地址，在设计中，针对不同的点数应设计不同的存储器存取地址，同时，在完成变换后，还要对开始输出有用信号的时刻进行指示。

６硬件的选择

本设计的硬件实现选用的是现场可编程门阵列（ＦＰＧＡ）来满足较高速度的需要。本系统在设计时选用的是ＡＬＴＥＲＡ公司的ＳＴＲＡＴＩＸ芯片，该芯片中包含有ＤＳＰ单元，可以完成较为耗费资源的乘法器单元。

同时，该器件也包含有大量存储单元，从而可保证旋转因子的精度。 除了一些专用引脚外，ＦＰＧＡ上几乎所有的引脚均可供用户使用，这使得ＦＰＧＡ信号处理方案具有非常好的Ｉ／Ｏ带宽。大量的Ｉ／Ｏ引脚和多块存储器可使设计获得优越的并行处理性能。其独立的存储块可作为输入／工作存储区和结果的缓存区，这使得Ｉ／Ｏ可与ＦＦＴ计算同时进行。

在实现的时间方面，该设计能在４０９６个时钟周期内完成一个４０９６点的ＦＦＴ。若采用１０ＭＨｚ的输入时钟，其变换时间在２００μｓ左右。而由于最新的ＦＰＧＡ使用了ＭｕｌｔｉＴｒａｃｋ互连技术，故可在２５０ＭＨｚ以下频率稳定地工作，同时，ＦＦＴ的实现时间也可以大大缩小。

ＦＦＴ运算结果的精度与输入数据的位数及运算过程中的位数有关，同时和数据的表示形式也有很大关系。一般来说，浮点方式比定点方式精度高。而在定点计算中，存储器数据的位数越大，运算精度越高，使用的存储单元和逻辑单元也越多。在实际应用中，应根据实际情况折衷选择精度和资源。

本设计通过ＭＡＴＬＡＢ进行仿真证明：其实现的变换结果与ＭＡＴＬＡＢ工具箱中的ＦＦＴ函数相比，信噪比可以达到６５ｄｂ以上，完全可以满足一般工程的实际应用要求。

作者：连冰，宫丰奎，张力，李兵兵

编辑：jq