什么是牛顿-拉夫逊方法?
牛顿其人:Isaac Newton(1642年12月25日– 1727年3月20日)是一位英国数学家,物理学家,天文学家,神学家和作家,被公认为有史以来最有影响力的科学家之一,并且是科学革命的关键人物。他的书《自然哲学的数学原理》于1687年首次出版,奠定了古典力学的基础。牛顿还为光学做出了开创性的贡献,并与戈特弗里德·威廉·莱布尼兹(Gottfried Wilhelm Leibniz)发展了无穷微积分的学科。
牛顿
拉弗森Joseph Raphson 生卒不详,其最著名的著作是1690年出版的《通用分析方程》。它包含一种方法,现在称其为牛顿-拉夫森方法,用于近似方程式的求根。艾萨克·牛顿(Isaac Newton)在1671年写的《通量法》中开发了一个非常相似的公式,但是这项工作要到1736年才出版,这是拉夫森分析之后近50年。但是,该方法的Raphson版本比Newton方法更简单,因此通常被认为是更好的方法。
所以,牛顿迭代法(简写)就是一种近似求解实数域与复数域求解方程的数学方法。那么这个方法是具体是什么原理呢?
牛顿迭代如何迭代?
直接看数学公式描述如何迭代不直观,先来看动图就很容易理解牛顿迭代法为什么叫迭代法以及怎样迭代的:
牛顿迭代法是原理是根据一个初始点在该点做切线,切线与X轴相交得出下一个迭代点的坐标,再在处做切线,依次类推,直到求得满足精度的近似解为止。
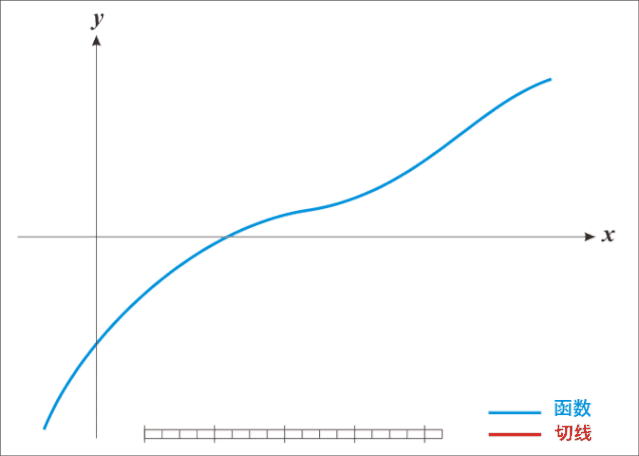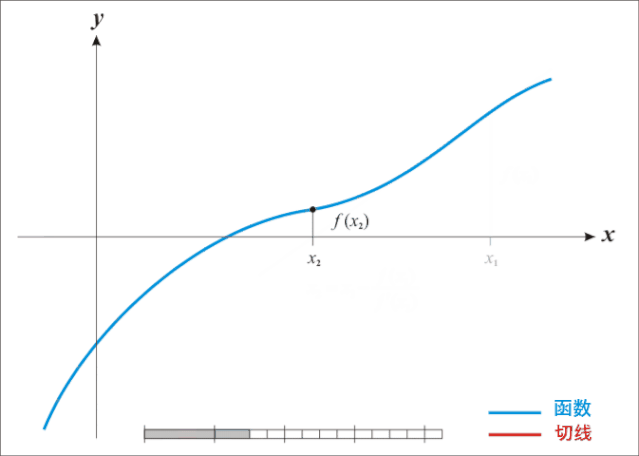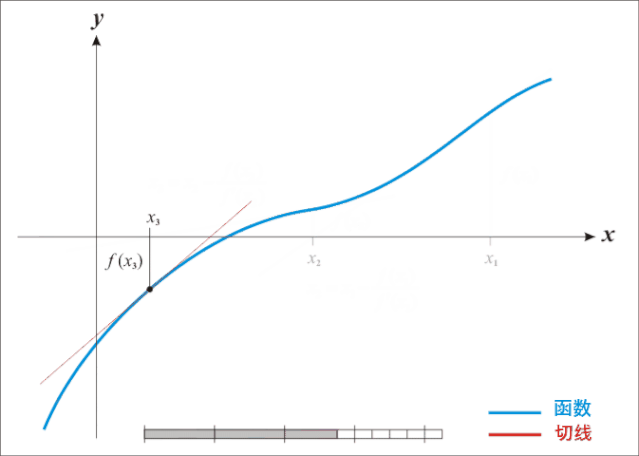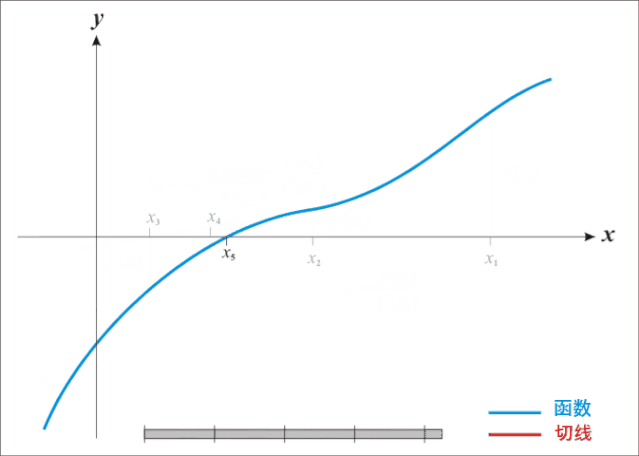
由前面描述知道,牛顿迭代法是用来近似求解方程的,这里有两个点需要说明:
为啥要近似求解?很多方程可能无法直接求取其解
迭代法非常适合计算机编程实现,实际上计算机编程对于牛顿迭代法广为应用
来看看,数学上如何描述的? 其中为函数在处的一阶导数,也就是该点的切线。 来简单推一推上面公式的由来,直线函数方程为: 知道一个直线的一个坐标点以及斜率则该直线的方程就很容易可以得知:那么该直线与轴的交点,就是也即等式的解:
啥时候停止迭代呢?
计算出
给出一个初始假定根值,利用上面迭代式子进行迭代
计算绝对相对迭代近似误差
将绝对相对近似误差与预定的相对误差容限进行比较。如果,则迭代步骤2,否则停止算法。另外,检查迭代次数是否已超过允许的最大迭代次数。如果是这样,则需要终止算法并退出。另一个终止条件是:
如何编码呢?
由于牛顿迭代法主要目的是解方程,当然也有可能用于某一个数学函数求极值,所以无法写出通用的代码,这里仅仅给出一个编代码的思路。相信掌握了思路,对于各种实际应用应该能很快的写出符合实际应用的代码。 假定一函数为 其波形图如下:
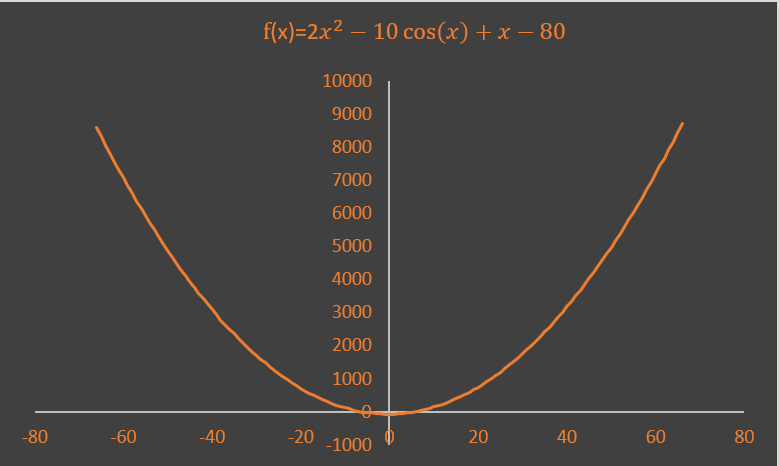
其一阶导数为: 那么对于该函数的根: 从图上大致可以知道有两个根,如果直接解方程,则很难求出其根,可以编个代码试试:
#include
需要注意些啥?
求斜率可能为0,如为0时,则可能找到了函数的极值,比如:
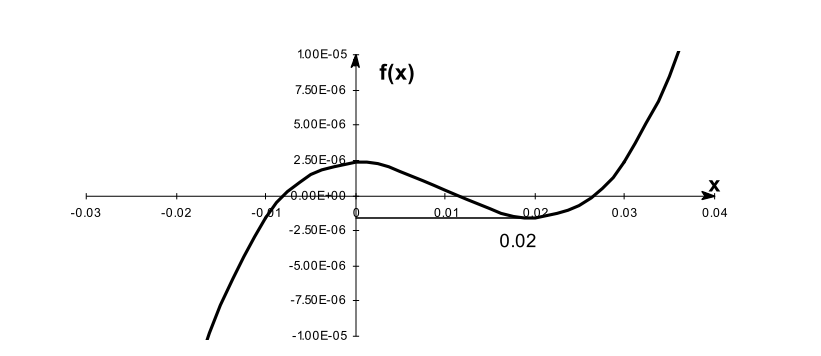
如果选择的初始猜测根的接近方程f(x)=0中函数f(x)的拐点 ,Newton-Raphson方法可能开始偏离根。然后,它可能会又收敛回到根。例如:

5435866
如果选择的初值不合适,可能会跳掉一些根,比如:

所以实际应用时,需要知道自己待求解模型的大致情况,在合理的加以调整。
有哪些应用?
比如知道某系统的传递函数,求解传函的参数,可以将上述方法推而广之,求解多维变量方程组,求导就变成求偏导了
又比如设计一电路测量某物质的阻抗
总结一下
牛顿迭代法在解决实际问题时,利用迭代求方程近似根的数学原理,在工程中有着很好的实用价值。比如求一个趋势的极值,传递函数参数辨识等都有广泛的实际应用。本文抛砖引玉,有可能文章也有很多错误疏漏的地方,如有不同看法或者发现错误,欢迎留言交流指正。
责任编辑人:CC
-
迭代法
+关注
关注
0文章
4浏览量
6395
原文标题:数学之美:牛顿-拉夫逊迭代法原理及其实现
文章出处:【微信号:elecfans,微信公众号:电子发烧友网】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
Labview 解析dxf文件并显示<一>
e203除法器算法改进(二)
如何理解工业物联网网关的协议解析功能
拉夫劳伦携手微软推出对话式AI应用购物助手Ask Ralph
捕捉微观世界的电子眼:汤姆逊散射诊断读出电子学解决方案

光学实验教具应用:迈克尔逊干涉仪实验
永磁同步电机二阶迭代学习控制
ADC技术的工作原理解析
继经典迈克尔逊干涉后的零差式激光干涉技术的出现

蓄电池放电原理解析
UPS电源的工作原理解析 UPS电源使用注意事项
SSM框架的源码解析与理解
防水测试仪的多样化测试方法:浸水法与气压法的深度解析






 牛顿拉夫逊迭代法的原理解析
牛顿拉夫逊迭代法的原理解析











评论