引言
DFT(Discrete Fourier Transformation)是数字信号分析与处理如图形、语音及图像等领域的重要变换工具,直接计算DFT的计算量与变换区间长度N的平方成正比。当N较大时,因计算量太大,直接用DFT算法进行谱分析和信号的实时处理是不切实际的。快速傅立叶变换(Fast Fourier Transformation,简称FFT)使DFT运算效率提高1~2个数量级。其原因是当N较大时,对DFT进行了基4和基2分解运算。FFT算法除了必需的数据存储器ram和旋转因子rom外,仍需较复杂的运算和控制电路单元,即使现在,实现长点数的FFT仍然是很困难。本文提出的FFT实现算法是基于FPGA之上的,算法完成对一个序列的FFT计算,完全由脉冲触发,外部只输入一脉冲头和输入数据,便可以得到该脉冲头作为起始标志的N点FFT输出结果。由于使用了双ram,该算法是流型(Pipelined)的,可以连续计算N点复数输入FFT,即输入可以是分段N点连续复数数据流。采用DIF(Decimation In Frequency)-FFT和DIT(Decimation In Time)-FFT对于算法本身来说是无关紧要的,因为两种情况下只是存储器的读写地址有所变动而已,不影响算法的结构和流程,也不会对算法复杂度有何影响。算法实现的可以是基2/4混合基FFT,也可以是纯基4FFT和纯基2FFT运算。
傅立叶变换和逆变换
对于变换长度为N的序列x(n)其傅立叶变换可以表示如下:
| N | nk | |
| X(k)=DFT[x(n)] = Σ x(n)W | ||
| n=0 | ||
式(1)
其中,W=exp(-2π/N)。 当点数N较大时,必须对式(1)进行基4/基2分解,以短点数实现长点数的变换。而IDFT的实现在DFT的基础上就显得较为简单了:
![]()
式(2)
由式(2)可以看出,在FFT运算模块的基础上,只需将输入序列进行取共轭后再进行FFT运算,输出结果再取一次共轭便实现了对输入序列的IDFT运算,因子1/N对于不同的数据表示格式具体实现时的处理方式是不一样的。IDFT在FFT的基础上输入和输出均有一次共轭操作,但它们共用一个内核,仍然是十分方便的。
基4和基2
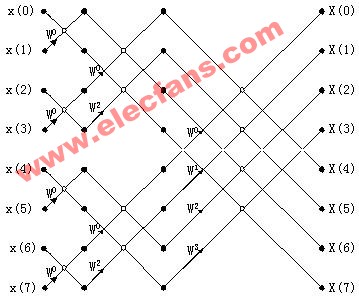
基4和基2运算流图及信号之间的运算关系如图1所示:
 |  |
(a)基4蝶形算法 | (b)基2蝶形算法 |
以基4为例,令A=r0+j×i0;B=r1+j×i1;C=r2+j×i2;D=r3+j×i3;Wk0=c0+j×s0:Wk1=c1+j×s1;Wk2=c2+j×s2;Wk3=c3+j×s3。分别代入图1中的基4运算的四个等式中有:
A'=[r0+(r1×c1-i1×s1)+(r2×c2-i2×s2)+(r3×c3-i3×s3)]+j[i0+(i1×c1+r1×s1)+(i2×c2+r2×s2)+(i3×c3+r3×s3)] 式(3)
B'=[r0+(i1×c1+r1×s1)-(r2×c2-i2×s2)-(i3×c3+r3×s3)]+j[i0-(r1×c1-i1×s1)-(i2×c2+r2×s2)+(r3×c3-i3×s3)] 式(4)
C'=[r0-(r1×c1-i1×s1)+(r2×c2-i2×s2)-(r3×c3-i3×s3)]+j[i0-(i1×c1+r1×s1)+(i2×c2+r2×s2)-(i3×c3+r3×s3)] 式(5)
D'=[r0-(i1×c1+r1×s1)-(r2×c2-i2×s2)+(i3×c3+r3×s3)]+j[i0+(r1×c1-i1×s1)-(i2×c2+r2×s2)-(r3×c3-i3×s3)] 式(6)
可以看出,式(3)至式(6)有多个公共项和类似项,这一点得到充分利用之后可以大大缩减基4和基2运算模块中的乘法器的个数,如上面A'至D'的四个等式中的这三对类似项:(r1×c1-i1×s1)与(i1×c1+r1×s1)、(r2×c2-i2×s2)与(i2×c2+r2×s2)、(r3×c3-i3×s3)与(i3×c3+r3×s3)以高于输入数据率的时钟进行时分复用,最终可以做到只需要3个甚至1个复数乘法器便可以实现。基2运算之所以采用图1-(b)中的形式进行基2运算,是为了将基本模块做成基4/2复用模块,它对于N有着更大的适用性和可借鉴性。在基4、基2和基4/2模块的基础上,构建基16、基8和基16/8模块有着非常大的意义。
算法实现
傅立叶变换实现时首先进行基2、基4分解,一般来说,如果算法使用基4实现,虽然使用的资源多了一些,但速度上的好处足以弥补。如果资源充足,使用基16、基8或基16/8复用模块,速度可以大大提高。一般FFT实现简单框图如图2所示。

在图2中,运算模块即为基2/4/8/16模块或它们的复用模块,Rom表中存储的是N点旋转因子表。控制模块产生所有的控制信号,存储器1和2的读写地址、写使能、运算模块的启动信号及因子表的读地址等信号。当然对于运算模块为基16/8复用模块时,控制模块就需要产生模式选择信号,如对于运算模块是基4/2模块时,该信号就决定了内部运算模块是进行基4运算还是基2运算。存储器1作为当前输入标志对应输入N点数据的缓冲器,存储器2作为中间结果存储器,用于存储运算模块计算出的各Pass的结果。在图中的各种地址、使能和数据的紧密配合下,经过一定延时后输出计算结果及其对应指示标志。图2只是一定点或浮点的FFT实现模块,如果是块浮点运算,则必须加入一个数据因子控制器,控制每遍运算过程中的数据大小,并根据各个Pass的乘性因子之和的大小,对最终输出进行大小控制,以保证每段FFT运算输出增益一致。
外部输入为N点数据段流和启动信号(N点之间如无间隔,则每N数据点输入一脉冲信号),一方面,外部数据存入存储器1中,同时通过控制模块的控制,读出存储器1中的前段N点数据和Rom表中的因子及相关控制信号送入运算核心模块进行各个Pass的运算,每个Pass的输出都存入存储器2中,最后一个Pass的计算结果存入存储器2中,并在下一个启动头到来后,输出计算结果。对图2的实现,除去运算模块,关键是各个Pass数据因子读写地址及控制信号的配合。
速度、资源和精度
假定输入数据的速率为fin,则每数据的持续时间T=1/fin,运算模块的计算时钟频率为fa,对于N(N=2p,p即为Pass数目)点FFT计算时延与Pass数目直接相关。如果使用基2运算不考虑控制开销,纯粹的计算时延为td=p×N×T×fin/fa。显然在fa>p× fin时,在N点内可完成FFT运算。否则不能完成,即不能实现流型的变换。这在N很大且输入数据速率较高时以FPGA实现几乎是不可能的,而且内部计算时钟过高容易导致电路的工作不稳定。设基2时的最小可流型工作运算频率为fa0,则使用基4实现流型的变换,计算时钟fa= fa0就可以。而使用基8时计算时钟fa= fa0便可完成,基16时为fa0的1/4。上面所讨论的是纯基运算,当N不为4的幂次方时(如N=2048=16×16×8,运算模块为基16/8复用模块),而又希望使用较低倍的时钟完成运算时,图2中的运算模块必然包括基4/2复用模块(即基16/8复用模块),这也就是前面提到复用模块的主要用意。由上面的分析可以得出结论,如果计算使用的基越大,完成速度越快。 但是,使用基16/8模块所使用的逻辑资源要比基4/2模块多将近一倍,这是因为基16/8复用模块是以基4模块和基4/2复用模块构建而成。当然,可以直接实现基16/8复用模块,但用FPGA很难解决复杂度和成本问题。另外,如果流型运算间隔比N点数据长度长一倍以上,可以考虑在较低的计算时钟下使用基2运算模块实现流型FFT。
运算结果的精度直接与计算过程中数据和因子位数(浮点算法)相关,如果中间计算的位数、存储数据位数和Rom表中的位数越大,输出精度就越大。当然,位数增大后逻辑运算资源和存储资源都会直线上升。
浮点、块浮点和定点FFT
根据运算过程中对数据位数取位和表示形式的不同,可以将FFT分为浮点FFT、块浮点FFT和定点FFT。它们在实现时对于系统资源的要求是不同的,而且有着不同的适用范围。
浮点FFT是基于数据表示为浮点的基础之上的,即数据是由一纯小数和一因子组成,输入要转成纯小数和因子的浮点表示形式,所有计算过程中保存应得计算结果大小,而输出要变成所需大小的定点表示形式。只要因子位数足够大,浮点FFT计算是不会溢出的。而定点则是所有计算过程中都是定点运算,如果各个Pass的截位规则不适当,很容易出现溢出,必须要有溢出控制。块浮点是介于它们之间的一种运算机制,它是根据本Pass的输入数据的大小,在计算之前进行控制(数据上移一比特或下移一比特或乘以一特定因子),可以保证不溢出,但一般也需要溢出控制。
浮点运算没有溢出,信号平均信噪比高,但由于因子的运算必然导致电路复杂,实现困难。定点运算实现简单,难以保证不溢出,需要统计得出合适的截位规则,否则溢出严重导致输出结果错误。块浮点由于每个Pass(包括最后输出前)结束后有一统计控制过程,延时较大,但是可以保证不溢出而且电路又相对浮点来说简单得多。 应根据具体应用的具体要求,选择合适的FFT。如果要求精度,并且要解决频域很高的单频干扰,就必须使用浮点的FFT,使用数据位数很大的定点和块浮点也能解决这个问题,但位数的确定十分困难。如果不要求高精度,逻辑资源和Rom比较紧张,可考虑定点运算。如果输入在频域集中于几个点上或者对精度要求一般,可以慢速处理,可以采用块浮点运算,就能够保证这几点的信噪比,而忽略其他点处的信噪比。
- 用FPG(5717)
- FT算法(5189)
相关推荐
FFT 算法的一种 FPGA 实现
FFT算法的FPGA实现
FFT的基本原理及算法结构
FFT至简设计法实现法_FFT算法_蝶形运算_fpga
FPGA实现高速FFT处理器的设计
DFT算法与FFT算法的优劣分析
HLS中FFT的反向输入算法不能实现
一种基于FPGA的可配置FFT IP核实现设计
一种基于Xilinx FPGA的电力谐波检测设计
基于FPGA的FFT算法硬件实现
基于FPGA的超高速FFT硬件实现
基于DSP的FFT算法实现
基于改进的CORDIC算法的FFT复乘及其FPGA实现
如何在FPGA上实现硬件上的FFT算法
嵌入式系统中怎么实现FFT算法?
浅谈实数FFT算法及其C语言的设计实现案
硬件实现EMD算法用那种架构比较好?
第32章 实数FFT的实现
基于FPGA的超高速FFT硬件实现
 26
26利用CORDIC 算法在FPGA 中实现可参数化的FFT
 9
9一种基于FPGA实现的FFT结构
 16
16基于Stratix系列FPGA 的FFT模块设计与实现
 19
19基于FPGA的FFT处理器的设计
 59
59基于FPGA的FFT处理器的研究与设计
 40
40利用CORDIC算法在FPGA中实现可参数化的FFT
 55
55一种块递推实时FFT算法模块设计与实现
 26
26利用FFT IP Core实现FFT算法
 6709
6709N为合数的FFT算法
 1436
1436
用FPGA实现FFT算法
 1426
1426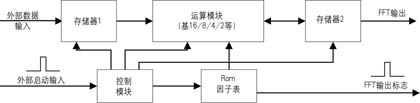
用C语言实现FFT算法
 6179
6179用FPGA实现FFT算法
 697
697
固定几何结构的FFT算法及其FPGA实现
 1004
1004
用FPGA实现FFT算法
 1105
1105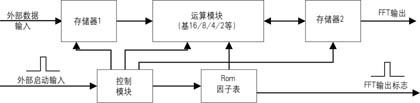
基于FPGA的高速定点FFT算法的设计方案
 992
992
基于FPGA的apFFT算法实现
 69
69基于改进FFT算法的OFDM调制解调模块设计
 40
40FPGA内嵌的块RAM在FFT算法中的应用
 54
54基于FPGA的高速高阶流水线工作FFT设计
 55
55高速高阶FPGA流水线工作FFT设计
 32
32基于并行FFT的pn码快速捕获算法实现
 35
35fft原理及实现
 203
203实数FFT算法的设计及其C语言实现
 10749
10749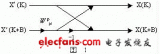
采用TMS320F2812的分裂基FFT算法的实现
 10
10FPGA的电力谐波检测的各部分电路组成及其设计与实现
 7
7数字信号处理技术FFT算法与FPGA的FFT变换设计
 20
20以FPGA实现FFT算法
 32
32fft算法是什么_如何提高fft算法分辨率
 7985
7985
基于FPGA的FFT实现方案
 11
11基于Xilinx FPGA 实现FFT算法的电力谐波检测的设计方案详解
 3391
3391
DSP芯片在基于FFT算法的电力系统谐波检测装置中的应用
 13
13基于FPGA-IPCore的FFT仿真与硬件实现
 2
2浅谈FFT算法原理 基于FPGA的FFT算法的硬件实现
 25530
25530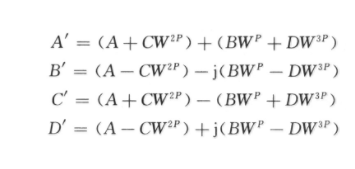
基于Quartus II的综合仿真实现FFT IP核的FFT算法
 8932
8932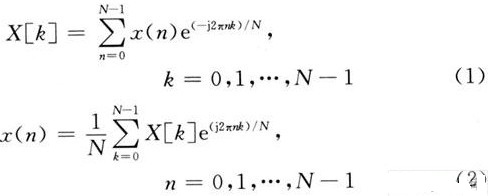
采用FPGA实现FFT算法
 17287
17287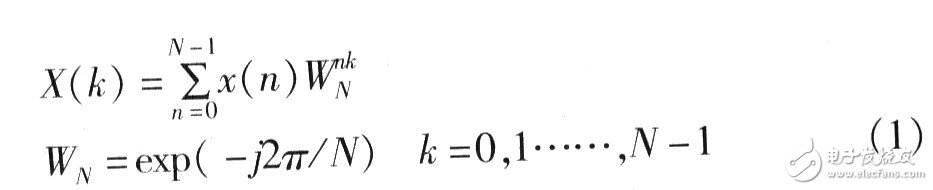
基于FPGA器件实现微波接力机中的FFT模块设计
 1191
1191
LTE物理上行共享信道中FFT算法分析与FPGA实现
 8
8使用FPGA实现流水线结构的FFT处理器论文讲解
 12
12如何使用FPGA和CPLD实现FFT算法与仿真分析
 19
19如何使用FPGA实现FFT的研究
 13
13如何使用FPGA实现基于修正Rife算法的正弦波频率估计
 7
7如何使用FPGA实现全并行结构FFT
 11
11用FPGA实现FFT算法的方法
 4515
4515傅里叶变换(FFT)的主要思想与算法
 3229
3229利用FFT算法实现快速傅里叶变换
 2632
2632采用FPGA实现FFT算法示例
 1649
1649
基2FFT的verilog代码实现及仿真
 630
630
从Xilinx FFT IP核到FPGA实现OFDM
 632
632
如何用FPGA实现FFT算法?
 445
445 电子发烧友App
电子发烧友App



















评论