如何用FPGA实现FFT算法？

点击上方蓝字关注我们

引言
DFT（Discrete Fourier Transformation）是数字信号分析与处理如图形、语音及图像等领域的重要变换工具，直接计算DFT的计算量与变换区间长度N的平方成正比。当N较大时，因计算量太大，直接用DFT算法进行谱分析和信号的实时处理是不切实际的。快速傅立叶变换（Fast Fourier Transformation，简称FFT）使DFT运算效率提高1～2个数量级。其原因是当N较大时，对DFT进行了基4和基2分解运算。FFT算法除了必需的数据存储器ram和旋转因子rom外，仍需较复杂的运算和控制电路单元，即使现在，实现长点数的FFT仍然是很困难。本文提出的FFT实现算法是基于FPGA之上的，算法完成对一个序列的FFT计算，完全由脉冲触发，外部只输入一脉冲头和输入数据，便可以得到该脉冲头作为起始标志的N点FFT输出结果。由于使用了双ram，该算法是流型（Pipelined）的，可以连续计算N点复数输入FFT，即输入可以是分段N点连续复数数据流。采用DIF（Decimation In Frequency）-FFT和DIT（Decimation In Time）-FFT对于算法本身来说是无关紧要的，因为两种情况下只是存储器的读写地址有所变动而已，不影响算法的结构和流程，也不会对算法复杂度有何影响。算法实现的可以是基2/4混合基FFT，也可以是纯基4FFT和纯基2FFT运算。
傅立叶变换和逆变换
对于变换长度为N的序列x（n）其傅立叶变换可以表示如下：
［td］N
［td］nk
［/tr］
X（k）=DFT［x（n）］=［td］Σ［td］x（n）W［/tr］
［td］n=0［td］［/tr］
式（１）
其中，W=exp（-2π/N）。
当点数N较大时，必须对式（1）进行基4/基2分解，以短点数实现长点数的变换。而IDFT的实现在DFT的基础上就显得较为简单了：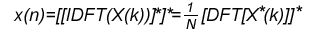
式（２）
由式（2）可以看出，在FFT运算模块的基础上，只需将输入序列进行取共轭后再进行FFT运算，输出结果再取一次共轭便实现了对输入序列的IDFT运算，因子1/N对于不同的数据表示格式具体实现时的处理方式是不一样的。IDFT在FFT的基础上输入和输出均有一次共轭操作，但它们共用一个内核，仍然是十分方便的。
基4和基2
基4和基2运算流图及信号之间的运算关系如图1所示：

（a）基４蝶形算法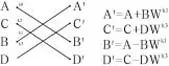
（b）基２蝶形算法
以基4为例，令A=r0+j×i0；B=r1+j×i1；C=r2+j×i2；D=r3+j×i3；Wk0=c0+j×s0：Wk1=c1+j×s1；Wk2=c2+j×s2；Wk3=c3+j×s3。分别代入图1中的基4运算的四个等式中有：
A‘=［r0+（r1×c1-i1×s1）+（r2×c2-i2×s2）+（r3×c3-i3×s3）］+j［i0+（i1×c1+r1×s1）+（i2×c2+r2×s2）+（i3×c3+r3×s3）］ 式（3）
B’=［r0+（i1×c1+r1×s1）-（r2×c2-i2×s2）-（i3×c3+r3×s3）］+j［i0-（r1×c1-i1×s1）-（i2×c2+r2×s2）+（r3×c3-i3×s3）］ 式（4）
C‘=［r0-（r1×c1-i1×s1）+（r2×c2-i2×s2）-（r3×c3-i3×s3）］+j［i0-（i1×c1+r1×s1）+（i2×c2+r2×s2）-（i3×c3+r3×s3）］ 式（5）
D’=［r0-（i1×c1+r1×s1）-（r2×c2-i2×s2）+（i3×c3+r3×s3）］+j［i0+（r1×c1-i1×s1）-（i2×c2+r2×s2）-（r3×c3-i3×s3）］ 式（6）
可以看出，式（3）至式（6）有多个公共项和类似项，这一点得到充分利用之后可以大大缩减基4和基2运算模块中的乘法器的个数，如上面A‘至D’的四个等式中的这三对类似项：（r1×c1-i1×s1）与（i1×c1+r1×s1）、（r2×c2-i2×s2）与（i2×c2+r2×s2）、（r3×c3-i3×s3）与（i3×c3+r3×s3）以高于输入数据率的时钟进行时分复用，最终可以做到只需要3个甚至1个复数乘法器便可以实现。基2运算之所以采用图1-（b）中的形式进行基2运算，是为了将基本模块做成基4/2复用模块，它对于N有着更大的适用性和可借鉴性。在基4、基2和基4/2模块的基础上，构建基16、基8和基16/8模块有着非常大的意义。
算法实现
傅立叶变换实现时首先进行基2、基4分解，一般来说，如果算法使用基4实现，虽然使用的资源多了一些，但速度上的好处足以弥补。如果资源充足，使用基16、基8或基16/8复用模块，速度可以大大提高。一般FFT实现简单框图如图2所示。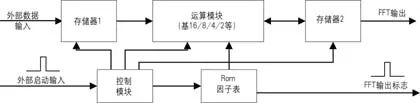

在图2中，运算模块即为基2/4/8/16模块或它们的复用模块，Rom表中存储的是N点旋转因子表。控制模块产生所有的控制信号，存储器1和2的读写地址、写使能、运算模块的启动信号及因子表的读地址等信号。当然对于运算模块为基16/8复用模块时，控制模块就需要产生模式选择信号，如对于运算模块是基4/2模块时，该信号就决定了内部运算模块是进行基4运算还是基2运算。存储器1作为当前输入标志对应输入N点数据的缓冲器，存储器2作为中间结果存储器，用于存储运算模块计算出的各Pass的结果。在图中的各种地址、使能和数据的紧密配合下，经过一定延时后输出计算结果及其对应指示标志。图2只是一定点或浮点的FFT实现模块，如果是块浮点运算，则必须加入一个数据因子控制器，控制每遍运算过程中的数据大小，并根据各个Pass的乘性因子之和的大小，对最终输出进行大小控制，以保证每段FFT运算输出增益一致。
外部输入为N点数据段流和启动信号（N点之间如无间隔，则每N数据点输入一脉冲信号），一方面，外部数据存入存储器1中，同时通过控制模块的控制，读出存储器1中的前段N点数据和Rom表中的因子及相关控制信号送入运算核心模块进行各个Pass的运算，每个Pass的输出都存入存储器2中，最后一个Pass的计算结果存入存储器2中，并在下一个启动头到来后，输出计算结果。对图2的实现，除去运算模块，关键是各个Pass数据因子读写地址及控制信号的配合。
速度、资源和精度
假定输入数据的速率为fin，则每数据的持续时间T=1/fin，运算模块的计算时钟频率为fa，对于N（N=2p，p即为Pass数目）点FFT计算时延与Pass数目直接相关。如果使用基2运算不考虑控制开销，纯粹的计算时延为td=p×N×T×fin/fa。显然在fa》p× fin时，在N点内可完成FFT运算。否则不能完成，即不能实现流型的变换。这在N很大且输入数据速率较高时以FPGA实现几乎是不可能的，而且内部计算时钟过高容易导致电路的工作不稳定。设基2时的最小可流型工作运算频率为fa0，则使用基4实现流型的变换，计算时钟fa= fa0就可以。而使用基8时计算时钟fa= fa0便可完成，基16时为fa0的1/4。上面所讨论的是纯基运算，当N不为4的幂次方时（如N=2048=16×16×8，运算模块为基16/8复用模块），而又希望使用较低倍的时钟完成运算时，图2中的运算模块必然包括基4/2复用模块（即基16/8复用模块），这也就是前面提到复用模块的主要用意。由上面的分析可以得出结论，如果计算使用的基越大，完成速度越快。
但是，使用基16/8模块所使用的逻辑资源要比基4/2模块多将近一倍，这是因为基16/8复用模块是以基4模块和基4/2复用模块构建而成。当然，可以直接实现基16/8复用模块，但用FPGA很难解决复杂度和成本问题。另外，如果流型运算间隔比N点数据长度长一倍以上，可以考虑在较低的计算时钟下使用基2运算模块实现流型FFT。
运算结果的精度直接与计算过程中数据和因子位数（浮点算法）相关，如果中间计算的位数、存储数据位数和Rom表中的位数越大，输出精度就越大。当然，位数增大后逻辑运算资源和存储资源都会直线上升。
浮点、块浮点和定点FFT
根据运算过程中对数据位数取位和表示形式的不同，可以将FFT分为浮点FFT、块浮点FFT和定点FFT。它们在实现时对于系统资源的要求是不同的，而且有着不同的适用范围。
浮点FFT是基于数据表示为浮点的基础之上的，即数据是由一纯小数和一因子组成，输入要转成纯小数和因子的浮点表示形式，所有计算过程中保存应得计算结果大小，而输出要变成所需大小的定点表示形式。只要因子位数足够大，浮点FFT计算是不会溢出的。而定点则是所有计算过程中都是定点运算，如果各个Pass的截位规则不适当，很容易出现溢出，必须要有溢出控制。块浮点是介于它们之间的一种运算机制，它是根据本Pass的输入数据的大小，在计算之前进行控制（数据上移一比特或下移一比特或乘以一特定因子），可以保证不溢出，但一般也需要溢出控制。
浮点运算没有溢出，信号平均信噪比高，但由于因子的运算必然导致电路复杂，实现困难。定点运算实现简单，难以保证不溢出，需要统计得出合适的截位规则，否则溢出严重导致输出结果错误。块浮点由于每个Pass（包括最后输出前）结束后有一统计控制过程，延时较大，但是可以保证不溢出而且电路又相对浮点来说简单得多。
应根据具体应用的具体要求，选择合适的FFT。如果要求精度，并且要解决频域很高的单频干扰，就必须使用浮点的FFT，使用数据位数很大的定点和块浮点也能解决这个问题，但位数的确定十分困难。如果不要求高精度，逻辑资源和Rom比较紧张，可考虑定点运算。如果输入在频域集中于几个点上或者对精度要求一般，可以慢速处理，可以采用块浮点运算，就能够保证这几点的信噪比，而忽略其他点处的信噪比。

有你想看的精彩

至芯科技FPGA就业培训班——助你步入成功之路、9月23号北京中心开课、欢迎咨询！

FPGA芯片在编程器烧录器里的应用

FPGA是什么（超级详细）

扫码加微信邀请您加入FPGA学习交流群

欢迎加入至芯科技FPGA微信学习交流群，这里有一群优秀的FPGA工程师、学生、老师、这里FPGA技术交流学习氛围浓厚、相互分享、相互帮助、叫上小伙伴一起加入吧！

点个在看你最好看

---

原文标题：如何用FPGA实现FFT算法？

文章出处：【微信公众号：FPGA设计论坛】欢迎添加关注！文章转载请注明出处。