量子机器学习入门：三种数据编码方法对比与应用

本文转自：DeepHub IMBA

---

在传统机器学习中数据编码确实相对直观：独热编码处理类别变量，标准化调整数值范围，然后直接输入模型训练。整个过程更像是数据清洗，而非核心算法组件。

量子机器学习的编码完全是另一回事。

传统算法可以直接消化特征向量[0.7, 1.2, -0.3]，但量子电路运行在概率幅和量子态的数学空间里。你的每个编码决策——是用角度旋转、振幅映射还是基态表示——都在重新定义信息在量子系统中的存在形式。这不是简单的格式转换，而是从根本上塑造了量子算法能够"看到"和处理的数据结构。

在量子机器学习中，编码不是预处理，而是算法设计的核心。

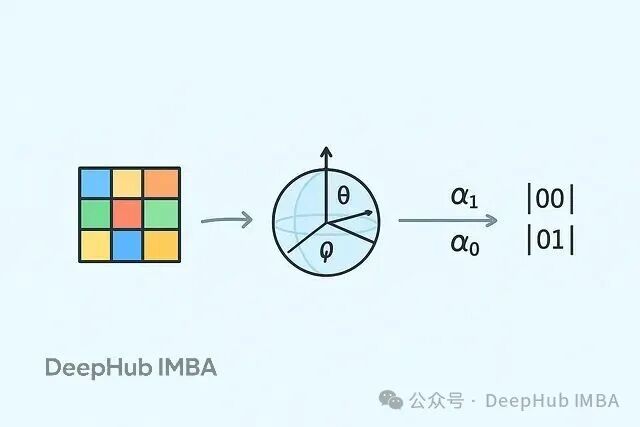
本文我们会详细讲解量子数据编码的三种主要方法，分析它们与传统方法的区别，以及为什么选对编码方式会决定你的量子模型成败。

---

量子编码的底层逻辑

量子电路处理数据的方式和传统算法截然不同，即使是在普通电脑上模拟运行也是如此。你没法直接把数值列表或者归一化向量塞给量子电路。数据必须先编码成量子态——这些数学对象可以模拟叠加和纠缠行为。这个编码过程就是连接经典数据集和量子计算环境的桥梁，让我们能在本地机器上做量子机器学习实验。

量子电路运行在一个完全不同的计算空间里。它们操作的是量子态，这些数学对象存在于叠加状态中，可以在多个量子比特之间形成纠缠，测量时会发生坍缩。量子电路处理不了2.3这样的普通数字，因为量子门操作的是概率幅和相位关系，不是经典的标量。

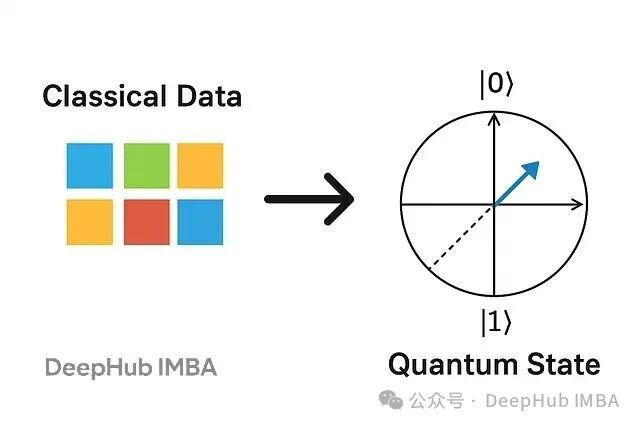
编码方法的选择从根本上决定了量子模型能学到什么。基础编码把数据直接映射成二进制量子态，实现简单但表达能力有限。振幅编码把整个数据集压缩进量子态的振幅里，效率很高但需要复杂的归一化处理。角度编码用量子门根据数据值旋转量子比特，在简单性和功能性之间找到了平衡点。

这个选择不只影响准确率，还决定了电路深度、量子比特需求，以及模型能利用哪些量子现象。选错了编码方式，即使是理论上有优势的量子算法也可能跑不过经典基线。

---

角度编码：最直观的映射方式

角度编码是把经典特征转换为量子态最直接的方法。每个特征值变成一个旋转角度，作用在对应的量子比特上。通常用RY门（绕Y轴旋转），因为它能让量子比特在Bloch球面的Y轴上旋转。

对于特征向量x = [x₁, x₂, …, xₙ]，角度编码的操作是：第一个量子比特RY(x₁)|0⟩ → cos(x₁/2)|0⟩ + sin(x₁/2)|1⟩，第二个量子比特RY(x₂)|0⟩ → cos(x₂/2)|0⟩ + sin(x₂/2)|1⟩，以此类推。

旋转角度直接控制量子比特在Bloch球面上的位置。角度0保持量子比特在|0⟩状态，π/2创建等权叠加(|0⟩ + |1⟩)/√2，π翻转到|1⟩状态。这种几何解释让角度编码很好理解——每个特征实际上在旋转对应的量子比特，把信息编码在量子态的几何结构里。

用Qiskit实现角度编码很简单。每个特征通过一个RY门处理，作用在独立的量子比特上：

from qiskit import QuantumCircuit
import numpy as np

class AngleEncoder:
def __init__(self, num_features):
self.num_features = num_features

def encode(self, features):
"""Encode a single feature vector into a quantum circuit."""
qc = QuantumCircuit(self.num_features)
for i, x in enumerate(features):
qc.ry(x, i)
return qc

处理批量样本只需要遍历数据集：

def batch_encode(encoder, data):
circuits = []
for features in data:
circuits.append(encoder.encode(features))
return circuits

想看编码后的量子态，Qiskit提供了可视化工具：

from qiskit.visualization import plot_bloch_multivector
from qiskit.quantum_info import Statevector

features = [np.pi/4, np.pi/2]
qc = AngleEncoder(len(features)).encode(features)

state = Statevector.from_instruction(qc)
plot_bloch_multivector(state)

这会在Bloch球面上画出每个量子比特的状态，让你直观看到数据是怎么嵌入的。

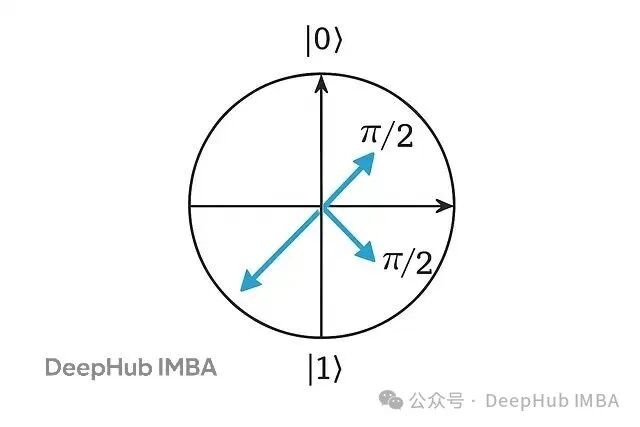
角度编码的优势很明显：特征到量子比特的映射很直接，适用于任何连续数据。但限制也不少，每个量子比特只能编码一个特征作为单个角度，表达能力有限。每个特征只影响一个量子比特，所以多特征之间的交互没法自然表示出来，也抓不到特征间的相关性。扩展到高维数据时需要很多量子比特这在实际应用中是个大问题。

---

振幅编码：量子优势的体现

振幅编码真正展现了量子计算的指数优势。它不是给每个特征分配一个量子比特，而是把整个特征向量压缩到量子态的振幅里。

比如特征向量x = [x₁, x₂, x₃, x₄]，振幅编码会创建量子态|ψ⟩ = α₁|00⟩ + α₂|01⟩ + α₃|10⟩ + α₄|11⟩，每个αᵢ对应一个归一化的特征值。这里的关键是指数信息密度：n个特征只需要log₂(n)个量子比特。256个特征的向量只要8个量子比特就够了，而角度编码需要256个。

但这种压缩有个硬性要求：Σ|αᵢ|² = 1，保证量子态的有效性。你的特征向量必须先归一化为单位长度。与角度编码直接映射不同，振幅编码需要复杂的数学预处理，把经典向量转换成概率幅。

这种指数压缩带来了独特的量子现象。特征不再独立它们存在于叠加态中，测量任何量子比特都会影响整个系统状态。这让量子算法能处理传统算法难以应对的特征相关性和高维模式，但也让编码的实现和理解变得复杂得多。

振幅编码面临两个角度编码没有的难题：归一化复杂性和电路深度问题。

归一化这步看起来简单，实际上很要命。你的特征向量必须满足Σ|αᵢ|² = 1，这直接影响模型对数据关系的解释。用L2归一化、先做min-max缩放再归一化，或者基于概率的归一化，对同一份经典数据会产生完全不同的量子表示。

负特征值更麻烦。量子概率幅可以是复数，但实现复振幅编码需要额外的量子比特或者复杂的相位编码。很多实际应用把振幅限制为实数，如果你的特征有重要的负值信息，就可能丢失关键信息。

电路深度是另一个坑。创建任意振幅状态需要复杂的量子电路，不像角度编码每个特征用一个RY门就完事。振幅编码需要一串受控旋转、受控NOT门，还要辅助量子比特。电路深度随特征数量对数增长，实现起来相当复杂。

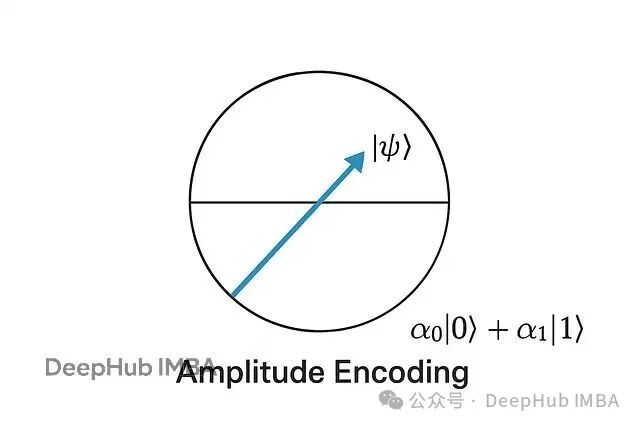
用Qiskit的initialize方法可以直接在量子比特上设置振幅：

from qiskit import QuantumCircuit

class AmplitudeEncoder:
def __init__(self, num_qubits):
self.num_qubits = num_qubits

def encode(self, features):
"""Encode normalized feature vector into quantum circuit."""
qc = QuantumCircuit(self.num_qubits)
qc.initialize(features, qc.qubits)
return qc

处理任意长度的数据集，需要结合归一化：

def encode_vector(vector):
vec = normalize(vector)
num_qubits = int(np.ceil(np.log2(len(vec))))
# Pad vector to length 2^num_qubits
pad_len = 2**num_qubits - len(vec)
padded = np.append(vec, [0]*pad_len)
return AmplitudeEncoder(num_qubits).encode(padded)

这样就能处理任意长度的向量，编码器会自动填充到最近的2的幂次。

---

基础编码：简单高效的离散表示

基础编码把分类数据直接映射到计算基础状态∣0⟩和∣1⟩。它不依赖叠加或干涉，而是用不同的正交状态表示不同类别，测量时能完美区分。

这创建了经典标签和二进制量子态的一对一映射。2量子比特系统有四个基础状态：∣00⟩,∣01⟩,∣10⟩,∣11⟩，可以表示四个类别。编码就是把分类标签转成二进制，然后初始化量子比特匹配这个二进制模式。类别"A"可能对应∣00⟩，类别"B"对应∣01⟩，测量时能100%确定地恢复原类别。

数学上很优雅：n个类别只需要 [log₂(n)] 个量子比特，对离散数据非常高效。

Qiskit实现基础编码很直接，把量子比特准备到对应的基础状态：

class BasisEncoder:
def __init__(self, num_qubits):
self.num_qubits = num_qubits

def encode(self, binary_string):
"""Prepare qubits in basis state from a binary string."""
qc = QuantumCircuit(self.num_qubits)
for i, bit in enumerate(binary_string):
if bit == "1":
qc.x(i) # Apply X gate to flip |0⟩ → |1⟩
return qc

多类问题可以把整数标签映射成二进制字符串：

def int_to_basis(n, num_qubits):
return format(n, f"0{num_qubits}b")

encoder = BasisEncoder(3)
qc = encoder.encode(int_to_basis(5, 3)) # Encodes integer 5 as |101⟩

基础编码对分类变量很合适，但处理连续或高维数据就效率太低了。编码大数据集会消耗太多量子比特，不实用。对数值特征，角度或振幅编码是更好的选择。

---

如何选择编码方式

选择哪种编码方式主要看你的具体需求。

如果你在学习量子机器学习基础，特征之间相对独立，需要简单易懂的电路，或者在NISQ设备上工作，角度编码是最好的起点。

如果你有高维连续数据，特征相关性很重要，能接受电路复杂度，想要最大化量子优势，振幅编码更合适。

如果数据主要是分类或离散的，需要完美的可解释性，要求最小电路深度，处理的是分类问题，基础编码是理想选择。

量子数据编码不只是预处理步骤，它从根本上定义了量子模型能学到什么、怎么学。选对编码方式，你的量子算法就有了成功的基础；选错了，再先进的量子算法也可能表现平平。

作者：Aadish Parate