傅里叶变换的数学原理主要基于一种将函数分解为正弦和余弦函数(或复指数函数)的线性组合的思想。以下是对傅里叶变换数学原理的介绍:
一、基本原理
- 傅里叶级数 :对于周期性连续信号,可以将其表示为傅里叶级数,即一系列正弦和余弦函数的线性组合。这是傅里叶变换的基础。
- 正交性 :正弦和余弦函数(或复指数函数)具有正交性,即在一定周期内,它们的内积为0。这使得它们成为理想的基底函数,用于表示和分解其他函数。
- 线性组合 :利用正交基底,可以将任意函数表示为这些基底函数的线性组合。在傅里叶变换中,这些基底函数是正弦和余弦函数(或复指数函数)。
二、傅里叶变换的定义
傅里叶变换是将一个函数从时域(或空间域)转换到频域的数学工具。根据原信号的不同类型,傅里叶变换可以分为四种类别:
- 非周期性连续信号 :傅里叶变换(Fourier Transform)。
- 周期性连续信号 :傅里叶级数(Fourier Series)。
- 非周期性离散信号 :离散时域傅里叶变换(Discrete Time Fourier Transform)。
- 周期性离散信号 :离散傅里叶变换(Discrete Fourier Transform)。
三、欧拉公式与复指数形式
欧拉公式e^ix=cosx+isinx提供了将正弦和余弦函数转换为复指数函数的方法。这使得傅里叶变换的表达式更加简洁和统一。在复指数形式下,傅里叶变换可以表示为一系列复指数函数的线性组合。
四、数学性质
- 线性算子 :傅里叶变换是线性算子,满足线性叠加原理。
- 逆变换 :傅里叶变换存在逆变换,可以将频域信号转换回时域信号。
- 卷积定理 :傅里叶变换可以简化卷积运算,将其转换为频域中的乘法运算。
- 能量守恒 :傅里叶变换保留了信号的能量信息,即原信号在时域中的能量等于变换后在频域中的能量。
五、应用领域
傅里叶变换在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用。例如,在信号处理中,傅里叶变换可以用于分析信号的频率成分;在图像处理中,傅里叶变换可以用于图像的滤波和增强等。
综上所述,傅里叶变换的数学原理基于正交基底和线性组合的思想,通过欧拉公式和复指数形式实现时域与频域之间的转换。其数学性质使得傅里叶变换成为科学、工程和数学等领域中不可或缺的工具。
-
函数
+关注
关注
3文章
4406浏览量
66838 -
时域
+关注
关注
1文章
80浏览量
29237 -
傅里叶变换
+关注
关注
6文章
444浏览量
43517
发布评论请先 登录
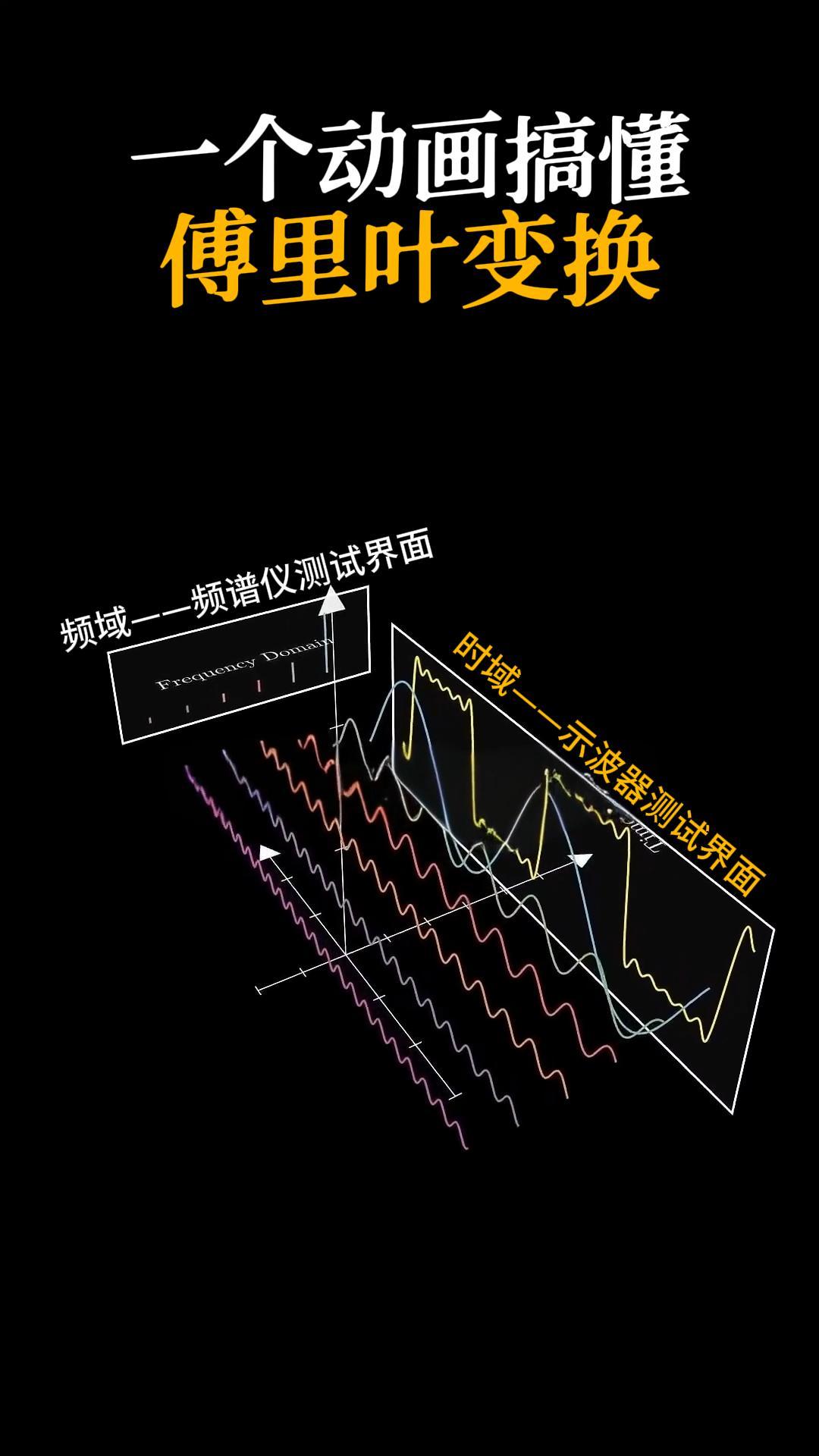
泰克示波器FFT功能详解

FFT快速傅里叶变换——方波及其谐波验证






 傅里叶变换的数学原理
傅里叶变换的数学原理












评论