谷歌AI最新发布的一篇论文给出了首个关于深度神经网络训练相关的理论证明,实验观察结果也为初步解释梯度下降强于贝叶斯优化奠定了基础。神经网络的理论面纱,正逐步被揭开。
原来,神经网络实际上跟线性模型并没那么大不同!
谷歌AI的研究人员日前在arxiv贴出一篇文章,给出了首个神经网络训练相关的理论证明。
实验中,他们将一个实际的神经网络训练过程与线性模型的训练过程相比,发现两者高度一致。这里用到的神经网络是一个wide ResNet,包括ReLU层、卷积层、pooling层和batch normalization;线性模型是用ResNet关于其初始(随机)参数的泰勒级数建立的网络。

将神经网络的训练过程与线性模型的相比,两者高度一致
在多个不同模型上试验并排除量化误差后,观察结果依旧保持一致。由此,谷歌AI研究人员得出结论,当学习率比较小且网络足够宽(不必无限宽)的时候,神经网络就是线性模型。
由此得出的一个推论是,使用梯度下降训练的大型网络集成能够用一个高斯过程描述,而且在梯度下降的任意时间都能用完备形式化描述这个高斯过程。
这些观察结果也构成了一个理论框架基础,可以用来初步解释长期以来困扰深度学习研究界的一个难题:梯度下降究竟在哪些情况下,具体是如何优于贝叶斯优化?
在训练深度神经网络被戏谑为“调参炼丹”的当下,这一发现犹如一道希望的强光,射进还被排除在“科学”之外的深度学习领域,激动人心。
相关论文:使用梯度下降训练的任意深度的Wide神经网络与线性模型的一致性
终于,调参不再是炼丹:首个关于神经网络训练的理论证明
基于深度神经网络的机器学习模型在许多任务中取得了前所未有的性能。通常,这些模型被认为是复杂系统,其中许多类型的理论分析是很棘手的。此外,由于控制优化的通常是高维的非凸损失平面(non-convex loss surfaces),因此要描述这些模型的基于梯度的训练动态机制具有挑战性。
就像在物理科学中常见的那样,研究这些系统的极限通常可以解释这些难题。对于神经网络来说,其中一个极限就是它的“无限宽度”(infinite width),指的是完全连接层中的隐藏单元数量,或卷积层中的通道数量。
在此限制下,网络初始化时的输出取自高斯过程(GP);此外,在使用平方损失进行精确贝叶斯训练后,网络输出仍然由GP控制。除了理论上的简单性,nfinite-width这一限制也具有实际意义,因为许多研究已经证明,更宽的网络可以更好地进行泛化。
在这项工作中,我们探索了梯度下降下宽的神经网络的学习动态机制(learning dynamics),并发现动态的权重空间描述变得非常简单:随着宽度变大,神经网络可以有效地被关于其初始化参数的一阶泰勒展开式(first-order Taylor expansion)取代。
对于这种诱导的线性模型,梯度下降的动态机制变得易于分析了。虽然线性化只在无限宽度限制下是精确的,但我们发现,即使是有限宽度的情况下,原始网络的预测与线性化版本的预测仍然非常一致。这种一致性在不同的架构、优化方法和损失函数之间都存在。
对于平方损失(squared loss),精确的学习动态机制允许封闭形式的解决方案,这允许我们用GP来描述预测分布的演化。这一结果可以看作是“先采样再优化”(sample-then-optimize)后验采样对深度神经网络训练的延伸。我们的经验模拟证实,该结果准确地模拟了具有不同随机初始化的有限宽度模型集合中预测的变化。
谷歌AI的研究人员表示,这篇论文的几大主要贡献包括:
首先,我们以 Jacot et al. (2018) 最近的研究成果为基础,该成果描述了在infinite width 限制下,整个梯度下降训练过程中网络输出的精确动态。他们的结果证明了参数空间的梯度下降对应于函数空间中关于新核的核梯度下降(kernel gradient descent),即Neural Tangent Kernel (NTK)。
我们工作的一个关键贡献是证明了参数空间中的动态等价于所有网络参数、权重和偏差集合中的仿射模型的训练动态。无论损失函数的选择如何,这个结果都成立。在平方损失的情况下, dynamics允许一个封闭形式的解作为时间函数。
无限宽(infinitely wide)神经网络初始化时的输出是高斯的,并且如Jacot et al.(2018)中所述,平方损失在整个训练过程中始终是高斯的。我们推导了该GP的均值和协方差函数的显式时间依赖表达式,并为结果提供了新的解释。
具体来说,该解释对梯度下降与参数的贝叶斯后验采样的不同机制提供了一种定量理解:虽然这两种方法都取自GP,但梯度下降不会从任何概率模型的后验生成样本。
这一观察结果与(Matthews et al.,2017)的“先采样后优化”(sample-then-optimize)框架形成了对比,在该框架中,只训练顶层权重,梯度下降从贝叶斯后验采样。
这些观察构成了一个框架,用来分析长期存在的问题,如梯度下降是否、如何以及在何种情况下提供了相对于贝叶斯推理的具体好处。
正如Chizat & Bach (2018b)中论述的,这些理论结果可能过于简单,无法适用于现实的神经网络。但是,我们通过实证研究证明了该理论在finite-width设置中的适用性,发现它准确地描述了各种条件下的学习动态机制和后验函数分布,包括一些实际的网络架构,如Wide Residual Network(Zagoruyko & Komodakis, 2016)。
具体实验:无限宽的神经网络就是线性模型
线性化网络(linearized network)
此处,我们将考虑线性化网络的训练动态,具体地说,就是用一阶泰勒展开代替神经网络的输出:
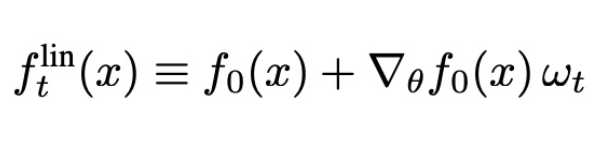
值得注意的是,flint是两项之和:第一项是网络的初始输出,在训练过程中保持不变;第二项是在训练过程中捕捉对初始值的变化。
使用这个线性化函数的梯度流的动态受到如下约束:
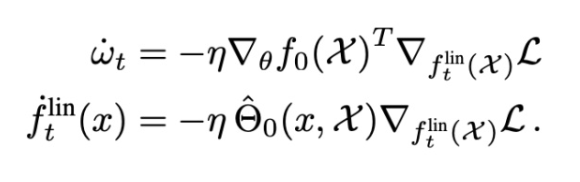
无限宽度限制产生高斯过程
当隐藏层的宽度接近无穷大时,中心极限定理(CLT)意味着初始化{f0(x)}x∈X时的输出在分布上收敛于多元高斯分布。这一点可以用归纳法非正式的进行证明。
因此,随机初始化的神经网络对应于一类高斯过程(以下简称NNGP),将有利于神经网络的完全贝叶斯处理。
梯度下降训练中的高斯过程
如果我们在初始化之后冻结变量θ≤L,并且只优化θ≤L+1,那么原始网络及其线性化是相同的。让宽度趋于无穷,这个特殊的tangent kernel的概率将收敛于K。这是用于评估高斯过程后验的“先采样后优化”方法的实现。
我们对比了NNGP、NTK-GP和NN集合的预测分布,如下图所示:
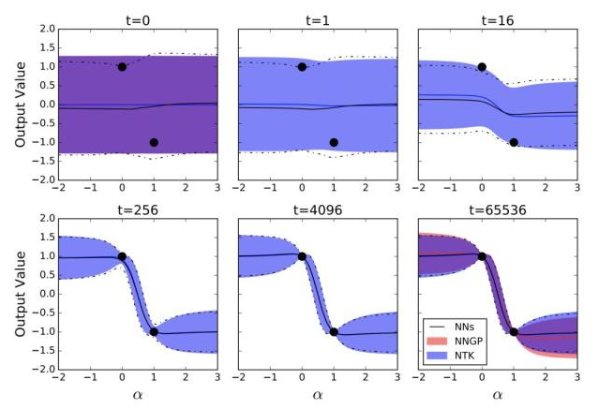
训练神经网络输出的均值和方差的动态遵循线性化的分析动态机制
黑线表示来自100个训练神经网络集合的预测输出分布的时间演变; 蓝色区域表示整个训练中输出分布的分析预测;最后,红色区域表示仅训练顶层的预测,对应于NNGP。
受过训练的网络有3个隐藏层,宽度为8192。阴影区域和虚线表示平均值的2个标准偏差。
无限宽度网络是线性化网络
原始网络的常微分方程(ODE)在一般情况下是不可解的。在积分函数梯度范数保持随机有界为n1,n2,…,nL→∞的技术假设下:
值得注意的是,上面公式中的上界只是理论性的,是根据经验观察得到的:
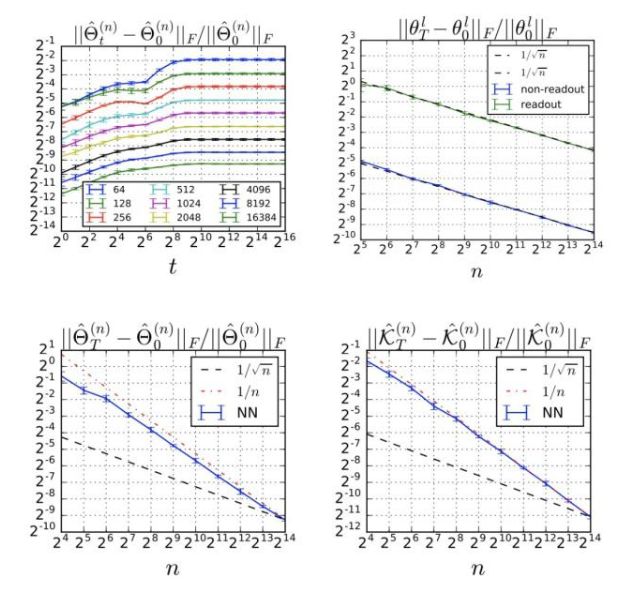
训练过程中Relative Frobenius范数的改变
在MSE设置中,我们可以对原始网络的输出与其线性化输出之间的差异进行上限:
对于非常宽的网络,我们可以用线性化动态机制来近似训练动态机制。
而从网络线性化中获得的另一个见解是,动态机制等效于随机特征法,其中,特征是模型相对于其权重的梯度。
-
神经网络
+关注
关注
42文章
4829浏览量
106828 -
梯度
+关注
关注
0文章
30浏览量
10549 -
机器学习
+关注
关注
66文章
8541浏览量
136241
发布评论请先 登录
NMSIS神经网络库使用介绍
在Ubuntu20.04系统中训练神经网络模型的一些经验
如何在机器视觉中部署深度学习神经网络
无刷电机小波神经网络转子位置检测方法的研究
基于FPGA搭建神经网络的步骤解析
BP神经网络的网络结构设计原则
BP神经网络与卷积神经网络的比较
如何优化BP神经网络的学习率
BP神经网络的优缺点分析
什么是BP神经网络的反向传播算法
BP神经网络与深度学习的关系
BP神经网络的基本原理
如何训练BP神经网络模型
深度学习入门:简单神经网络的构建与实现
人工神经网络的原理和多种神经网络架构方法
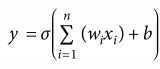





 首个关于深度神经网络训练相关的理论证明
首个关于深度神经网络训练相关的理论证明











评论