傅里叶变换的数学意义

傅里叶变换的数学意义

傅里叶变换是一种数学工具，它是一种将一个函数在一个频域转换为另一个函数在另一个频域中的操作。傅里叶变换起源于1807年，由法国数学家让·巴蒂斯特·约瑟夫·傅里叶提出，它是一种将一个函数拆分成若干个正弦函数的方法，并将每个正弦函数的振幅、相位和频率表示出来，从而对原函数进行分析的方法。

傅里叶变换是物理学、工程学和数学领域中广泛使用的一个工具，它被应用于信号处理、图像处理、量子力学、电子学、物理学和声学等多个领域。在计算机科学中，傅里叶变换用于处理数字信号，并在许多领域中被广泛使用，例如音频处理、图像处理、视频压缩、通信和控制等方面。

傅里叶变换的数学定义是将一个函数f(x)分解成无穷多个正弦函数和余弦函数的和，即：

$f(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}F(k)e^{ikx}dk$

其中，F(k)表示一个复数函数，称为f(x)的傅里叶变换。k是一个实数变量，表示频率。

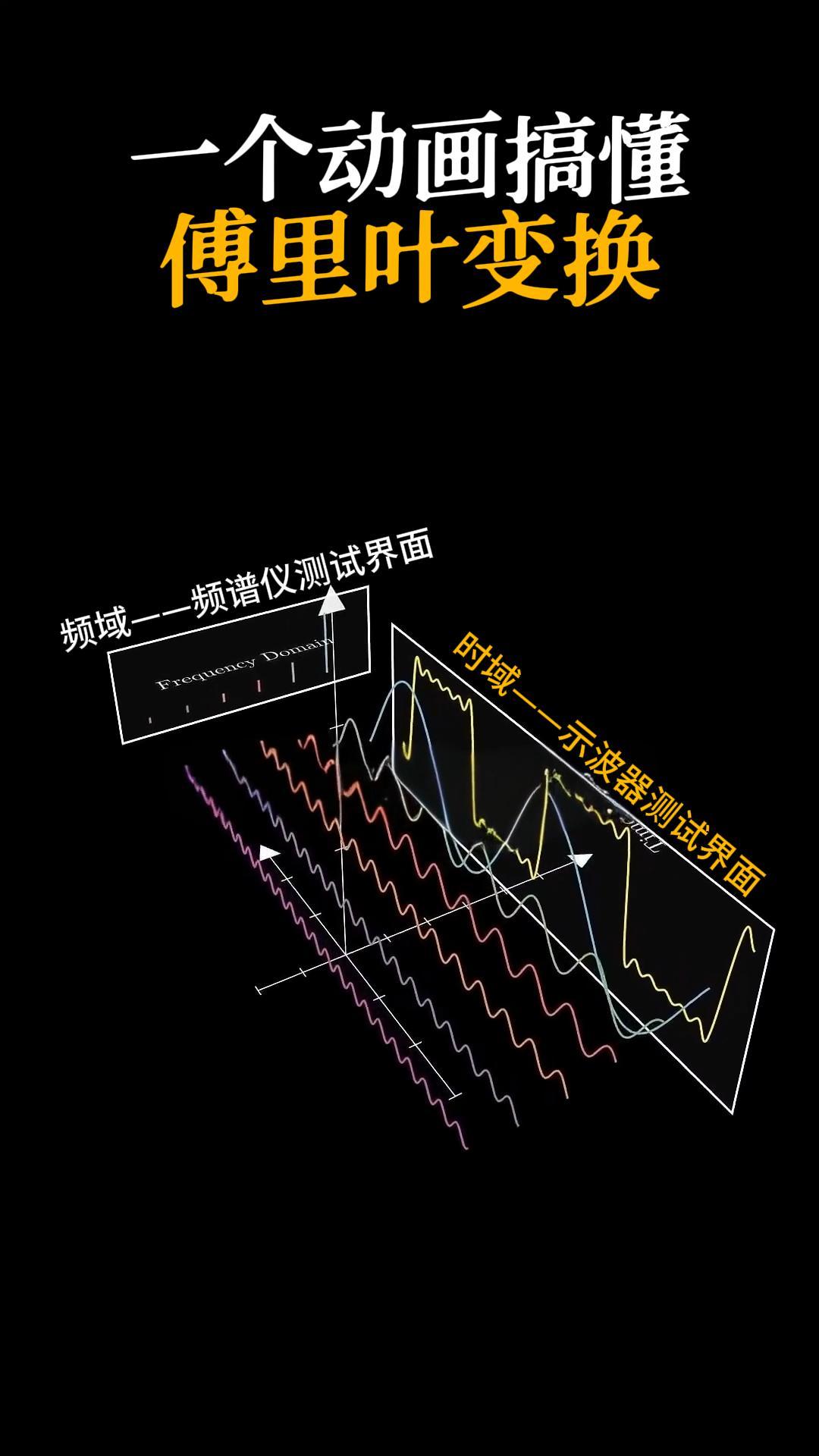
傅里叶变换的数学意义是将时间域中的信号转换为频率域表示，这样可以更好地了解信号所包含的信息。在时间域中，函数f(t)表示信号随时间的变化情况，而在频域中，函数F(ω)表示信号中所包含的频率分量。

以音频信号为例，当一个人说话时，嘴巴的振动产生声音，这种声音随时间变化。我们可以将这个信号表示为一个函数f(t)，其中t表示时间。但是，这个函数往往包含许多不同频率的分量，我们无法在时间域中直接分析这些分量。通过使用傅里叶变换，我们可以将f(t)分解为一个频域表示F(ω)，其中ω表示频率。这样我们可以更好地理解信号中包含的不同频率的分量。

傅里叶变换的理解有助于更好地理解一些与计算机数据处理相关的概念。例如，一个计算机数字音频文件可以通过傅里叶变换转换为在时间域中显示并以可视化形式呈现。这可以帮助人们更好地理解数字音频文件的工作原理，并且可以用于比较它们之间的相似性或不同之处。

傅里叶变换的主要应用是在时域和频域之间的转换，它可以帮助我们更好地了解信号中所包含的频率成分。它还可以应用于数字信号处理和通信领域，通过傅里叶变换可以对信号进行滤波、降噪和频率分析等操作，从而提高信号的质量和可靠性。

总之，傅里叶变换是一种非常有用的数学工具，可以将一个函数在时域和频域之间转换，并且可以用于信号处理、图像处理、量子力学、电子学、物理学和声学等领域。它对计算机数据处理的发展和理解具有重要意义，可以帮助我们更好地了解数字信号的特性，提高信号的质量和可靠性。