信号与系统中卷积分析和总结

“卷积”是信号与系统时域分析中的一个重要内容。本文对此知识点进行了详细的分析和总结，并给出了多道例题及详细解答。

（一）常用信号的卷积表

首先，将常用信号的卷积、以及卷积的性质整理成表格，这些信号的卷积，需要熟练掌握其计算方法，并且要记住结果。为了方便大家对比，帮助理解和记忆，我把连续时间信号的卷积积分与离散时间信号的卷积和放在同一张表格中。

（二）卷积的计算

卷积的计算方法有以下几种：

定义法；

性质法；

图解法；

竖式法（卷积和）

需要注意的是，这几种计算方法，不是孤立的，经常需要结合运用。

例题1：

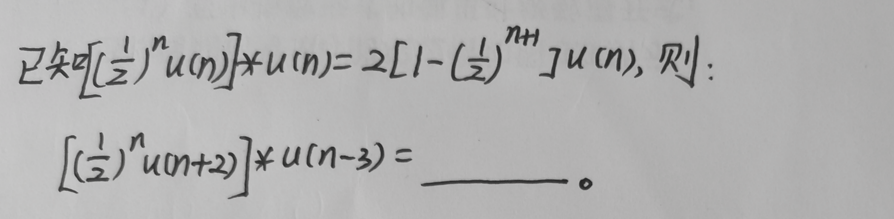
【分析】

这是一道填空题，如果不给题设中的条件，也可以直接计算出结果，但既然已经给了题设的条件，就不需要利用公式再去求解计算，而只需要利用卷积的时移特性。

【解答】

例题2：

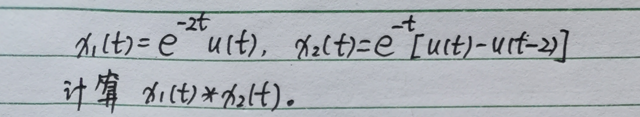
【分析】

此题是一道典型的求解卷积积分的题目，一个有限长信号与一个单边信号卷积题目难度不大，属于基本题。可以直接利用卷积积分的定义式计算，也可以利用图解法。

【解答】

方法一：

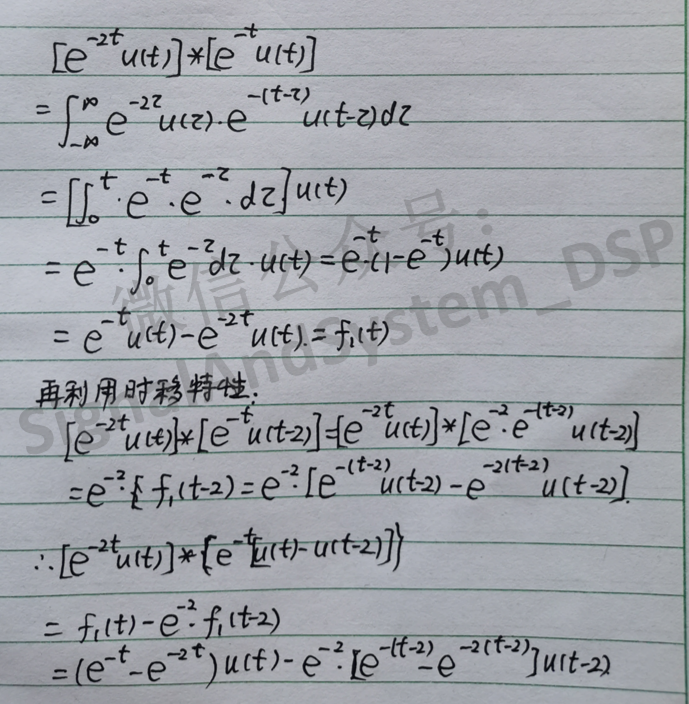
方法二：

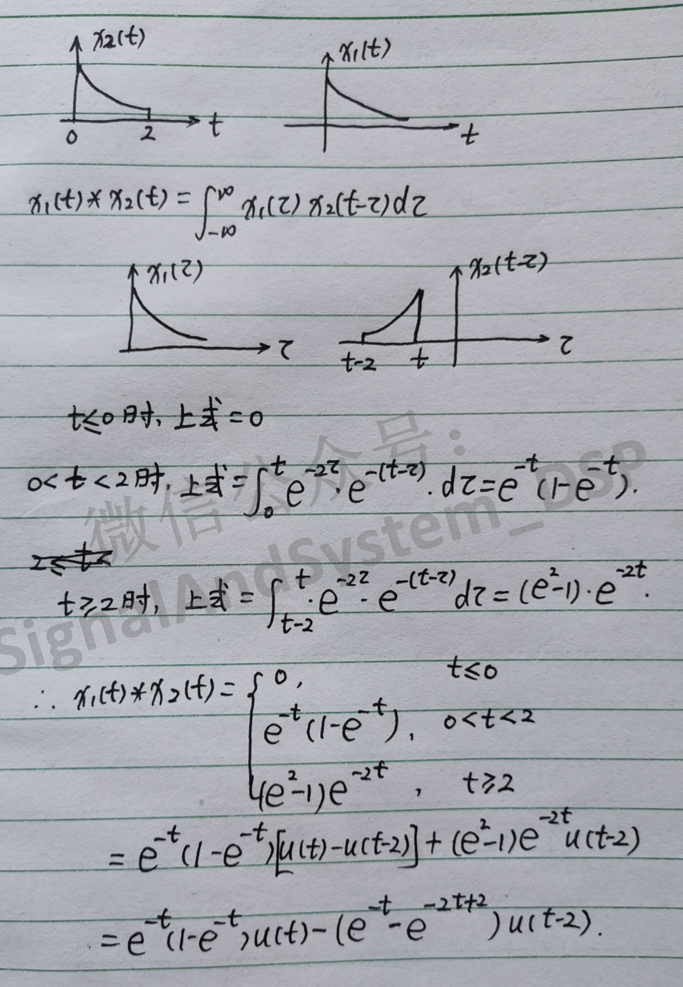
【总结】

有限长信号或者单边信号卷积，关键是判断被积函数公共的非零区间。

结果通常为分段函数，可以写成分段的表示形式，也可以利用阶跃信号，写成一个表达式。

例题3：

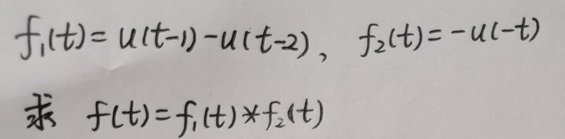
【分析】

此题也是一道典型的卷积积分计算题，与例题2类似之处是，也是一个有限长信号与一个单边信号卷积。但例题2中为右边信号，而此题中为左边信号。与例题2相比，难度稍大。此题可以直接从定义式出发计算，也可以利用图解法计算。正确解题的关键是：判断被积函数的共同的非零区间。

【解答】

f(t) 的图形如下图：

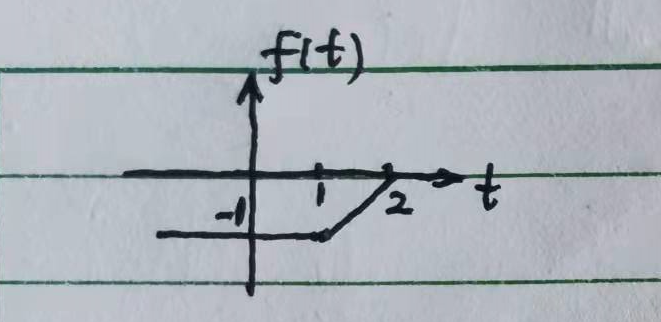
当然，最终结果也可以写成闭合表达式：

或者也可以写为：

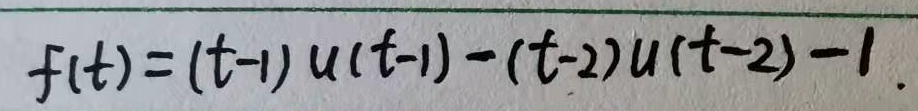
例题4：

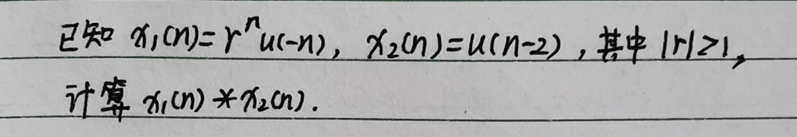
【分析】

此题是一道典型的离散卷积和计算的题目。可以利用卷积和的定义式计算，也可以利用 z 变换来求解。

【解答】

方法一：利用卷积和的定义式计算

注意，上图中，（1）式和（2）式中的边界条件，即可以写成n＞2和n≤2，也可以写成n≥2和n＜2，这样，写成闭合表达式就有两种形式，这两种形式的答案，实质是相同的。

方法二：利用 z 变换的方法。

注意，利用z变换来求解，一定要写清楚收敛域，否则计算反变换时容易出错。

【总结】

（1）右边序列与左边序列的卷积和，结果为双边序列；

（2）卷积和的最终结果，通常有多种不同的形式，但形式不同，本质相同。

例题5：

【分析】

这是一道很有趣的题目。需要用卷积的一些基本概念进行灵活分析，而不是死记硬背式的计算。

考察卷积的两个知识点：第一个，两个有限长序列的长度与卷积得到的序列长度之间的关系；第二个，卷积的竖式法。

【解答】

根据题意，序列 x(n) 共10个点，记为 L1 = 10；序列 h(n) 共 N+1 个点，记为 L2 = N+1。则卷积结果 y(n)的长度 L = L1 + L2 - 1 =N+10。

序列x(n)在 n = 0~9 内函数取值均为1，h(n) 在 n=0~N内函数取值均为1，而 y(14)等于0，说明序列 y(n) 的长度不大于14，即：

L= N+10≤ 14，即 N≤4

再根据 y(4)= 5，结合竖式法，可以推断：N = 4。验证如下：

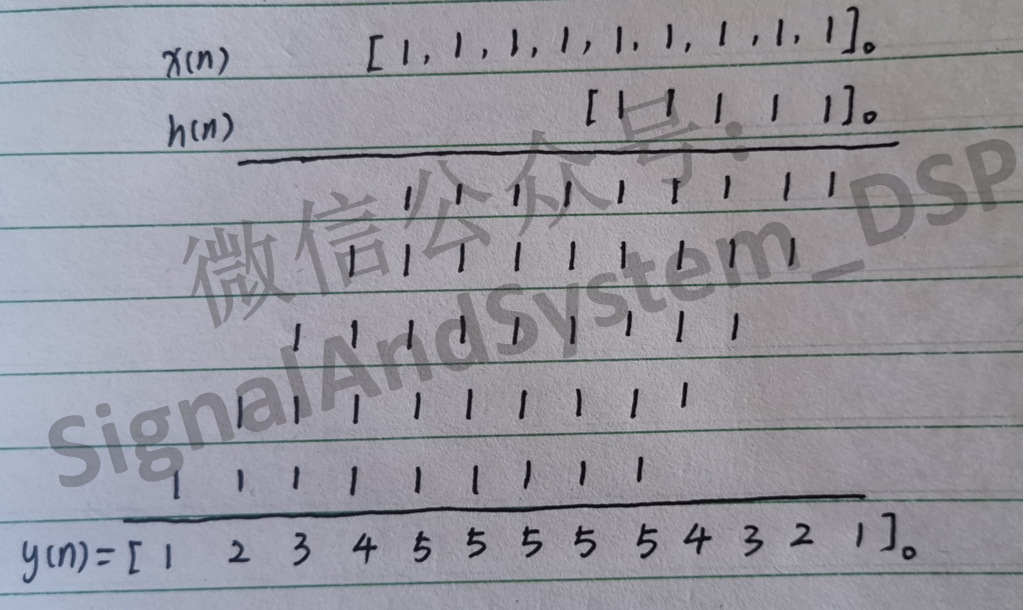
【总结】

（1）在解决有限长序列的卷积时，竖式法经常是一种简单的方法；

（2）两个有限长序列的卷积，卷积结果也是有限长的，其长度等于两个序列的长度之和减1。

例题6：

已知 x(t)*h(t) = y(t)，证明

x(-t)*h(-t) = y(-t)。

【分析】

此题有两种方法，第一种方法是，直接利用卷积的定义式证明；第二种方法是，利用傅里叶变换来证明。

【解答】

方法一：

方法二：

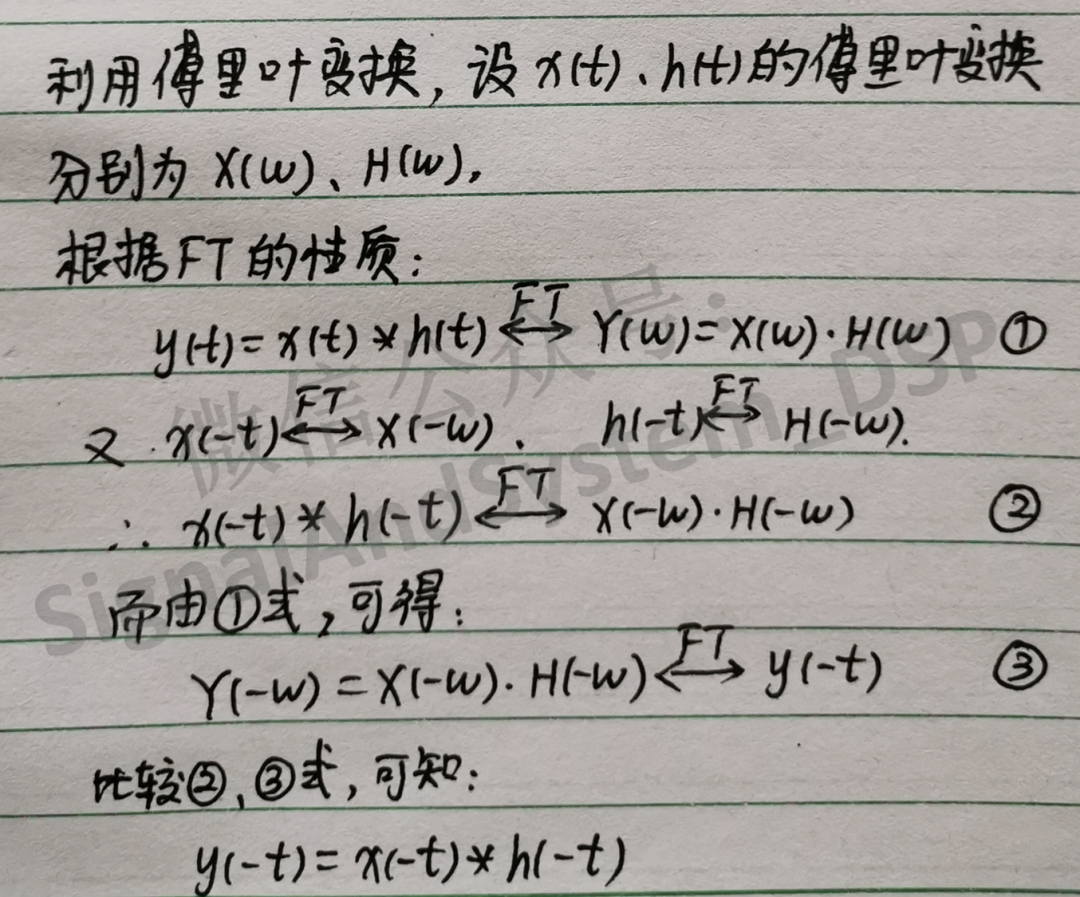
【总结】

（1）注意在运用卷积定义式时，注意下面两个式子，第一种写法对，第二种写法错：

（2）采取此题方法，可以得出以下结论：

x(at)*h(at)=1/|a|×y(at)

（三）卷积的物理含义

卷积的存在，有它的特殊意义，卷积之所以在信号与系统课程中如此重要，正是因为它的物理含义：

卷积，揭示了LTI系统的零状态响应与输入信号、系统单位冲激响应之间的关系，即：

零状态响应 = 输入信号 * 系统单位冲激响应

例题7：

【分析】

此题需利用卷积的物理含义进行分析。有两种方法。

【解答】

方法一：利用单位冲激响应的概念，令输入信号 x(t) 等于单位冲激信号，带入积分式中，则得到 h(t)。

方法二：利用卷积的概念，将题目中的积分式与卷积公式对照，得出 h(t)。

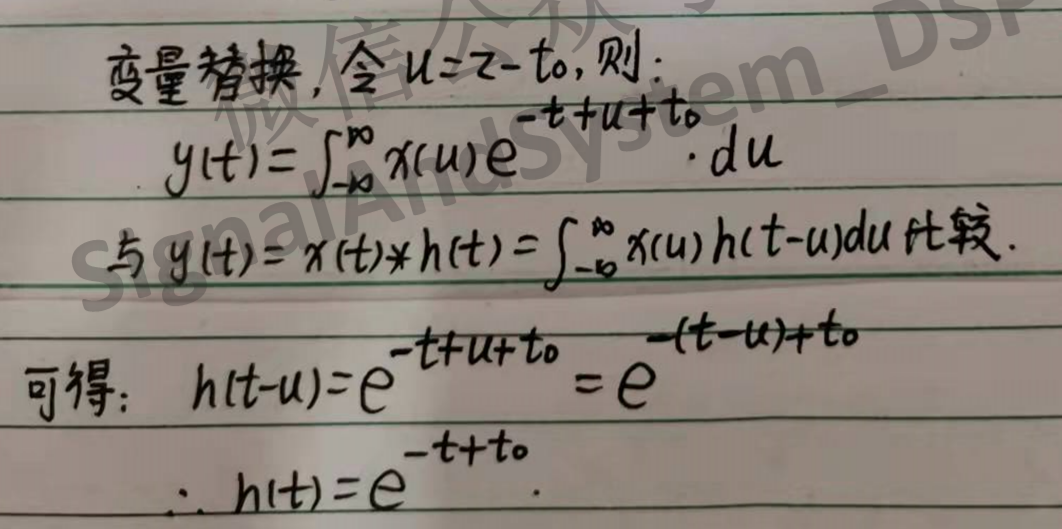
例题8：

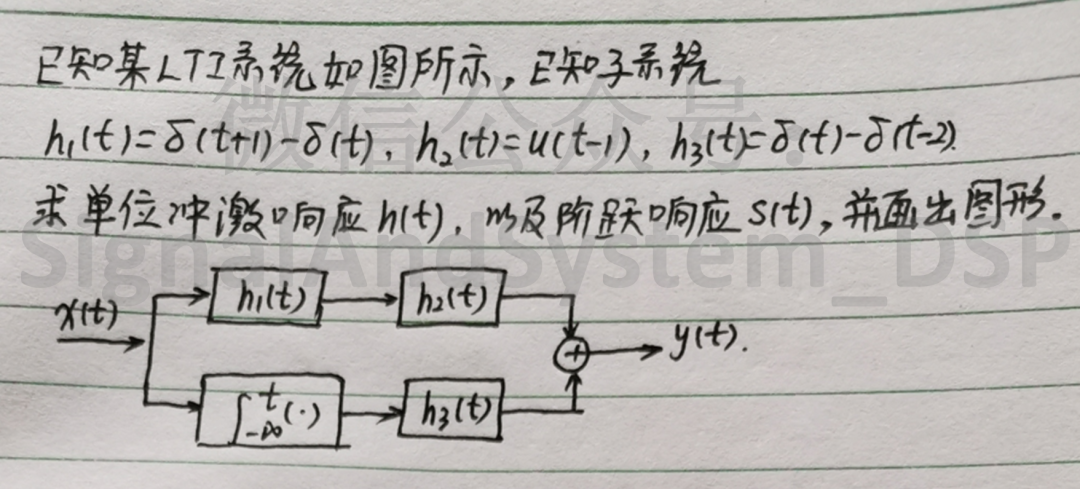
【分析】

此题用到的知识点：

（1）串联系统的单位冲激响应，等于各个分系统的单位冲激响应之卷积，并联系统的单位冲激响应，等于各个分系统的单位冲激响应之和；

（2）积分器的单位冲激响应就是 u(t)；

（3）单位阶跃响应 s(t) 与单位冲激响应 h(t) 之间的关系为：h(t) 是 s(t) 的微分，s(t) 是 h(t) 的积分。

【解答】

（四）后续章节中与卷积相关的知识点总结

卷积在信号与系统课程中扮演着重要角色，除了时域分析之外，在课程后续章节的多个知识点中，都有卷积的身影。大家一定要灵活处理。例如：

（1）一个域相乘，另外一个域卷积

（2）周期冲激串的傅里叶变换

（3）周期信号的傅里叶变换与主周期信号傅里叶变换之间的关系

（4）时域/频域抽样

（5）单边周期信号的拉氏变换、单边周期序列的 z 变换

另外，在数字信号处理课程中，也要用到卷积的概念，例如：DFT分析信号频谱、窗函数法和频率抽样法设计FIR滤波器、脉冲响应不变法设计IIR滤波器等。

由于篇幅关系，就这个问题不再展开。