探究比特对编码与比特对编码乘法器的设计

比特对编码与比特对编码乘法器的设计

今天一起看看比特对编码（有的也把它称为基4booth编码，名字不重要，主要是思想），可以解决上文中提到的问题

比特对编码原理

booth重编码的主要问题在于不能过滤掉010这样序列。故考虑将通过连续相邻两位进行编码，每次从低位向高位移动1位的方式（即booth比编码），变成连续相邻3位进行编码，每次从低位向高位移动2位的方式（比特对编码）。先讨论其原理。

一个数我们考虑从低位向高位对其进行编码，使其变成4进制（基4）的表示形式，每两位二进制表示一位的四进制数。

3（2'b11）比4少1，2(2'b10)比4少2。在4进制数中，2需要向前进位则需要减去2再向前进位；3需要向前进位则需要减去1再向前进位。

我们的比特对编码就是基于上述原理来的。

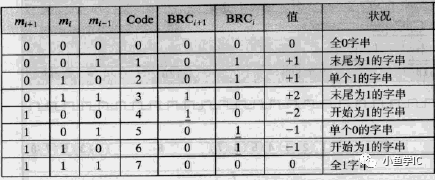
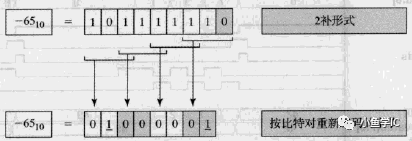
下面给出比特对编码规律，如下表和图所示，图为一个实例，是对1011_1111的编码，其表示-65。比特对编码结果为 -1 00-1,故其表示的十进制d为：

d=-4^3 -4^0= -65

再举个例子，比如对0001_1001进行比特对编码，得到编码为：

+2-2+1

故其表示的十进制计算如下：

d=2*(4^2) -2*(4^1) +4^0

=32+8+1=41

其中的乘2与乘4都可以通过移位操作来实现，这就是为什么需要这么编码的原因。

可以看到，每相邻三位进行编码，其中的最低位mi-1 其实表示来自前面的进位。故当其为 001时，得到的编码为 +1(表示4)，011时最低位1表示进位，故编码为1+1=+2。

从中可以得出，对于8位二进制数0101_0101，经过比特对编码后，得到的是 +1 +1 +1 +1，其表示的数为：

4^3 + 4^2 + 4^1 + 4^0 =

64+16+4+1=85

此时只需要进行3次加法运算，不会存在booth编码所存在的问题。

同时发现对于数据位宽非偶数的数，我们需要将其在最高位补填一位符号位，再进行比特对编码。

比特对编码（对乘数进行编码）乘法器，需要进行的加法次数为乘数位宽的一半。

比特对编码乘法器设计

设计思想概叙：定义位宽为DW_A+DW_B+2的product寄存器（DW_A为被乘数a的位宽，DW_B为乘数b的位宽）。当in_valid与in_ready同时为高时，将乘数b（位宽为b）加载到product的低DW_B位。然后在计算状态下（executing），将每次加法器的输出放到product的高位，并每个时钟周期将product右移2位。每个时钟周期，通过对

m={product[1:0],prd_r[1]}

（其中prd_r[1]为上一个时钟product的第二位）进行编码，得出本次操作是加1、加2，减1，减2，还是不用做加减法（编码为0）（代码中上述五种操作对应的标志信号分别为add_1,add_2,sub_1,sub_2，noneed_add）。并将加法结果每次存到product寄存器的高位。

这里有个巧妙的思想就是，每个时钟周期通过对product右移2位，再将其高DW_A位与a或者a*2进行相加或者相减操作，正好相当于每次product不动，把a或者a*2左移2位（乘以4）。这个思想源于《Verilog HDL 高级数字设计》中的精简寄存器时序乘法器设计。

注意，这里是有符号数乘法器，每次左移需要在高位补符号位，故左移不能简单的用 >> 描述（>>左移默认高位填0），具体描述见代码。

其中减法采用加上这个数的补码的方式；通过一个计数器（cnt）来指示什么时候结束运算；其中运算控制状态机采用《状态机的第四种描述方式》编写；条件选择多采用与或方式实现。

设计Verilog如下（dff_with_en为寄存器）：

module radix4_mul #( parameter DW_A = 16, parameter DW_B = 8)( input clk, input rst_n, input in_valid, output in_ready, input flush, output o_valid, input o_ready, input [DW_A-1:0] a, input [DW_B-1:0] b, output [DW_A+DW_B-1:0] mul_res); //state machine for mulwire state;wire [$clog2((DW_B+1)/2):0] cnt;

wire exe_cnt_final = (cnt == (DW_B+1)/2); wire execute_en = in_valid&in_ready; localparam GET_DATA = 1'b0;localparam EXECUTING = 1'b1; wire curr_get_data = (state == GET_DATA);wire curr_executing = (state == EXECUTING); wire is_executing = curr_executing & (~exe_cnt_final);

wire nxt_get_data_en = (curr_executing & exe_cnt_final & o_ready) | flush;wire nxt_executing = curr_get_data & execute_en; wire nxt_state = (nxt_get_data_en & GET_DATA) | (nxt_executing & EXECUTING); wire tran_en = nxt_get_data_en | nxt_executing; dff_with_en #( .DW(1))dff_state( .clk (clk), .rst_n (rst_n), .enable (tran_en), .d_in (nxt_state), .q_out (state)); //cnt//wire [$clog2((DW_B+1)/2):0] cnt_nxt = curr_executing ? cnt+1 : 'h0; dff_with_en #( .DW($clog2((DW_B+1)/2)+1))dff_cnt( .clk (clk), .rst_n (rst_n), .enable (1'b1), .d_in (cnt_nxt), .q_out (cnt));

//get the awire [DW_A-1:0] a_d;wire [DW_A-1:0] nxt_a_d = nxt_executing ? a : a_d; dff_with_en #( .DW(DW_A))dff_a( .clk (clk), .rst_n (rst_n), .enable (1'b1), .d_in (nxt_a_d), .q_out (a_d));//radix 4 codingwire prd_r;wire [DW_A+DW_B+1:0] product;//wire [DW_B-1:0] b_shift;wire [2:0] m = is_executing ? {product[1:0],prd_r} : 3'b000; wire add_1 = (m == 3'b001) | (m == 3'b010);wire add_2 = (m == 3'b011);wire sub_1 = (m == 3'b110) | (m == 3'b101);wire sub_2 = (m == 3'b100); //wire [DW_A+DW_B+1:0] product; wire [DW_A+1:0] adder_op1 = ( {DW_A+2{add_1}}& { {2{a_d[DW_A-1]}},a_d} ) | ( {DW_A+2{add_2}}& { {1{a_d[DW_A-1]}},a_d,1'b0} ) | ( {DW_A+2{sub_1}}& (~{ {2{a_d[DW_A-1]}},a_d}) ) | ( {DW_A+2{sub_2}}& (~{ {1{a_d[DW_A-1]}},a_d,1'b0})); wire add_en = (add_1 | add_2 | sub_1 | sub_2)& is_executing;

wire noneed_add = is_executing & (~(add_1 | add_2 | sub_1 | sub_2)); wire [DW_A+1:0] adder_op2 = product[DW_A+DW_B+1:DW_B]; wire adder_cin = sub_1|sub_2; wire [DW_A+1:0] adder_res = adder_op1 + adder_op2 + adder_cin; wire [DW_A+DW_B+1:0] nxt_product = ({DW_A+DW_B+2{add_en}} &{{2{adder_res[DW_A+1]}},adder_res,product[DW_B-1:2]})| ({DW_A+DW_B+2{noneed_add}} & {{2{product[DW_A+DW_B+1]}},product[DW_A+DW_B+1:2]}) | ({DW_A+DW_B+2{o_valid}} & product) | ({DW_A+DW_B+2{nxt_executing}} & {{DW_A+2{1'b0}},b}); dff_with_en #( .DW(DW_A+DW_B+2))dff_product( .clk (clk), .rst_n (rst_n), .enable (1'b1),

.d_in (nxt_product), .q_out (product)); wire prd_nxt = curr_get_data ? 1'b0 : product[1]; dff_with_en #( .DW(1))dff_prd( .clk (clk), .rst_n (rst_n), .enable (1'b1), .d_in (prd_nxt), .q_out (prd_r));assign in_ready = curr_get_data;assign o_valid = exe_cnt_final;assign mul_res = product[DW_A+DW_B-1:0]; endmodule

如果乘数b位宽为奇数，请补一位符号位，变成偶数位宽，再输入。

编辑：jq