基本数学运算在FPGA中的实现算法仿真分析

作者：没落骑士

一、前言

FPGA以擅长高速并行数据处理而闻名，从有线/无线通信到图像处理中各种DSP算法，再到现今火爆的AI应用，都离不开卷积、滤波、变换等基本的数学运算。但由于FPGA的硬件结构和开发特性使得其对很多算法不友好，之前本人零散地总结和转载了些基本的数学运算在FPGA中的实现方式，今天做一个系统的总结归纳。

二、FPGA中的加减乘除

1.硬件资源

Xilinx 7系列的FPGA中有DSP Slice ，叫做“DSP48E1”这一专用硬件资源，这是一个功能强大的计算单元，单就用于基本运算的部分有加减单元和乘法器。详见参考文献1.

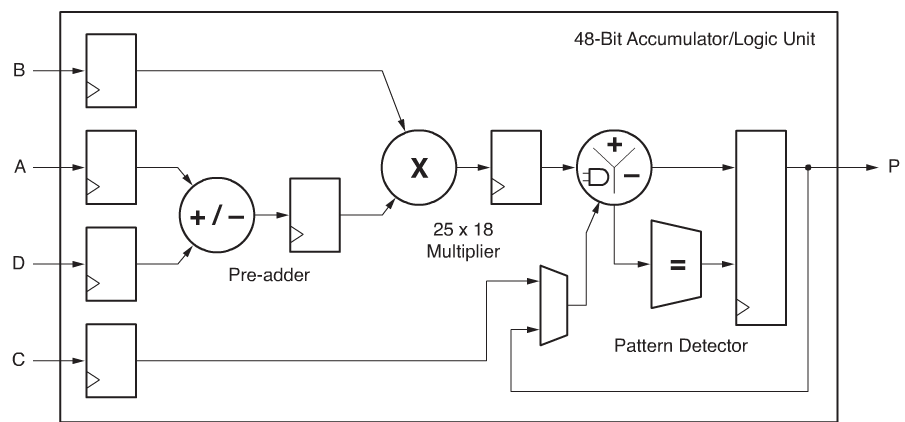
因此可以直接用HDL语言中的加、减、乘符号实现变量与常量间运算操作以及变量与变量间操作。而四则运算中的除法没有基本的逻辑计算单元可以对应，因此计算除法需要调用除法器IP核。

2.确认数据的表示范围

有符号数：（补码）-2^(N-1) ~ 2^(N-1)-1 如N = 8，则表示范围是：-128 ~ 127.

无符号数：0~2^N-1 如N = 8，则表示范围是：0~255.

定点数：2Q13 范围是：-4~4-2^(-13) 精度是：2^(-13)

3.结果有效位宽

首先讨论结果位宽问题。在FPGA中往往采用定点运算替代浮点运算来降低硬件资源占用率和计算延迟，其中的精髓就是精度与资源的权衡。若按照保留计算结果的全部精度，N bit数与Mbit数相加结果需要N+1bit（N>M）。N bit数与M bit数相乘之积需要N+M bit。而减法可以转化为加法，除法则转换为乘法和加减法的组合。如果操作数是定点小数，则在满足以上准则的前提下，A与B相加（A小数点位数>B小数点位数），结果小数点位数与A相同；A与B相乘（小数点位数分别为p和q），结果小数点位数是p+q。

4.定点运算步骤

然而（话锋一转），在大多数场合下，不需要以上这么多位来保留计算结果，因为我们在进行数学运算时，已经知道输入数据的大致范围，一个数除以1000和除以1结果数据所需最小位宽能一样么？加减运算的操作步骤是先对齐小数点位数，后加减。而乘法是先计算后取小数点。这实际上与十进制运算一致，我们看看具体的计算步骤：

整数之间加减以及乘法的统一步骤：预估结果位宽N --> 按照结果位宽扩展操作数符号位以防止溢出 --> 运算取低N位。

定点小数加减运算步骤：预估结果位宽N --> 得到结果小数点后位数 --> 对齐操作数整数位和小数位，确定扩展位宽M（M≥N） --> 加减运算取低M位。

定点小数乘法运算步骤：预估结果位宽N --> 得到结果小数点后位数 --> 扩展操作数位宽 --> 相乘取低N位

5. 变量与常量运算化简

以上讨论的均是两变量之间的运算规则，当然结果位宽及格式准则是适用的。变量与常量的运算的优势在于，可以将乘除法转换成加减以及移位运算实现，从而降低计算复杂度和延迟。当常数项C为2的整数次幂（C = 2^p），则乘C等于变量左移p位，除以C等于变量右移p位。几个在书中看到的几个简单示例：A*16 = A >1A除以3 = A*(0.25+0.0625+0.0156) = A>>2+A>>4+A>>6A除以5 = A*(0.125+0.0625+0.0156) = A>>3 + A>>4 + A>>6.其中乘法完全等价对应的移位相加操作，而除法的移位代替会损失精度。

三、如何计算特殊函数

FPGA内部的DSP Slice可以直接进行最基本的加法和乘法运算，但是对于其他比如对数、指数、三角函数、开根号等特殊函数就无能为力了。这时需要借助算法对这些特殊函数进行变换和简化。FPGA实现复杂函数的常用手段一个是级数展开，再一个就是CORDIC算法。关于CORDIC的理论知识和具体内容详见参考文献2，这里主要阐述CORDIC的IP核调用以及应用示例。CORDIC算法就是通过一定的手段，将很多复杂的特殊函数变为相加移位运算，这一点对于硬件芯片实现来说非常友好。CORDIC分为旋转模式和矢量模式，配合圆周坐标、线性坐标和双曲线坐标会有六种组合，具体见下表：

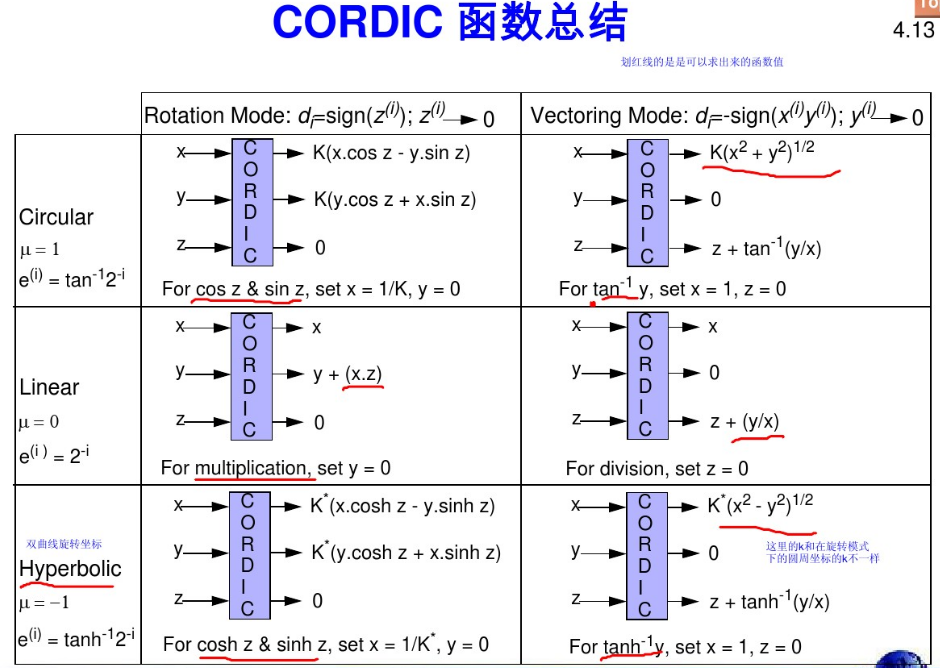
从表中发现，基本的乘除法、三角函数、反三角函数、双曲函数、反双曲函数、开根号都能够直接求得，那其他函数怎么办？

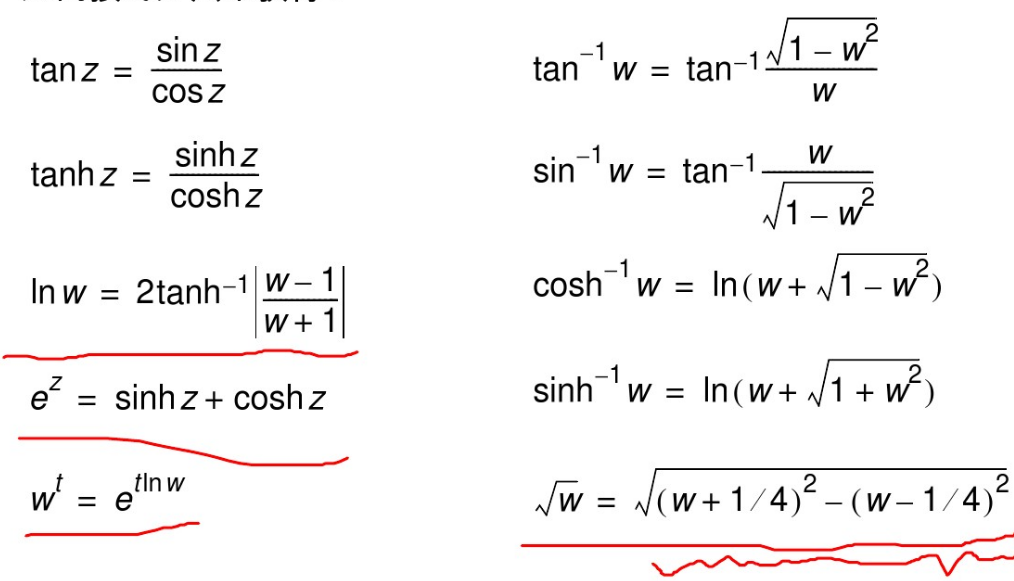
常见的函数计算需求基本都能满足，虽上述变换式对自变量定义域有限制，但同样可以分析输入数据的取值范围并利用简单的数学变换得到想要的结果。Xilinx同时提供了浮点IP核以及CORDIC IP核，前者调用简单但占用资源大，延迟高，因此利用CORDIC算法计算函数是个较好的选择。

四、CORDIC计算e^x Demo

1. 算法仿真分析

要计算e^x数值需要让CORDIC工作在双曲坐标的旋转模式下，通过e^x = sinhx+coshx关系式间接求得。首先看下sinh和cosh函数的曲线，有个直观认识。

我们用MATLAB毫不费力地验证一下公式正确性：

在设计后也同样要借助MATLAB进行仿真验证。

2. CORDIC IP核

现在通过查看user guide得知CORDIC IP核的接口及主要特性。

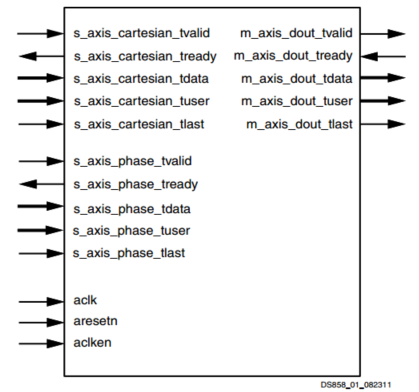
接口包括输入笛卡尔数据输入通道、相位输入通道、全局信号以及数据输出通道。该IP核有两种结构：串行和并行，可根据数据吞吐量需求选择，并行结构可以每个时钟输出一个计算结果。如果计算sinh和cosh，要向phase通道输入相位信息，X_OUT是cosh(phase),Y_OUT是sinh(phase).输入phase必须满足数据范围，否则出现不可预计结果。输出帧结构及数据范围如下：

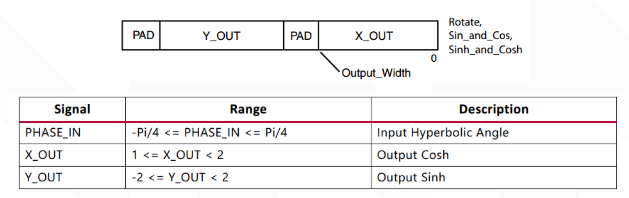
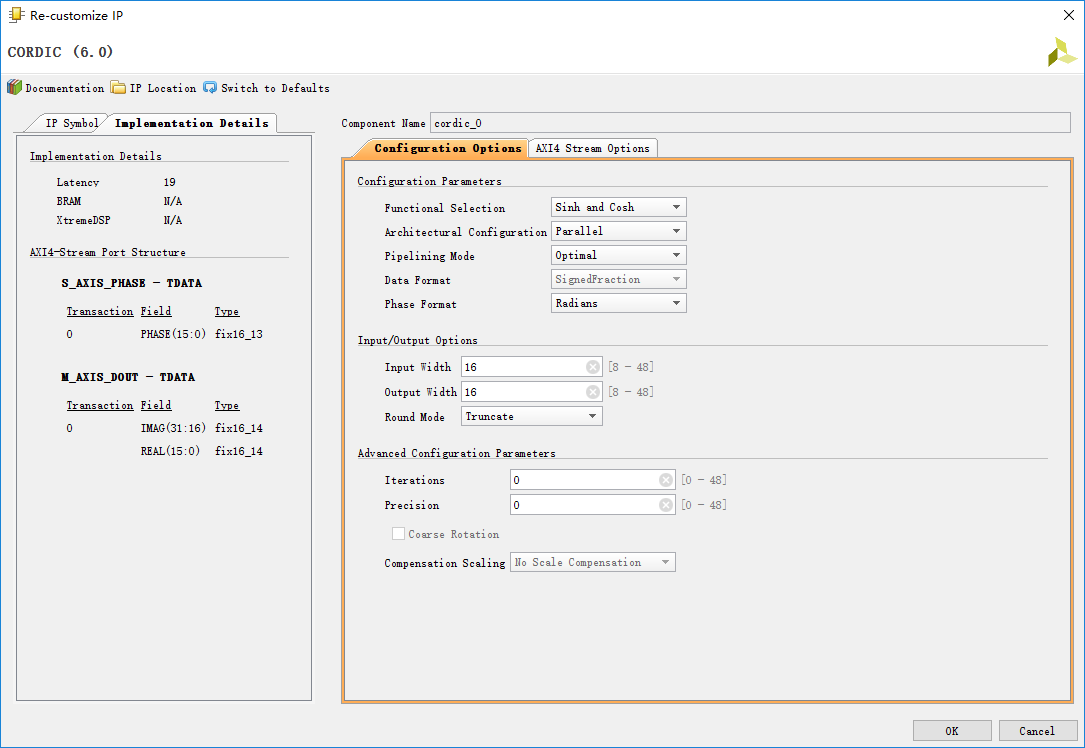
其中输入数据格式为2QN，输出则是1QN。由于均是有符号数，也就是输入整数部分3bit，输出整数部分2bit。接下来对IP核进行配置，重点是第一页，此处将其配置为计算sinh和cosh模式，采用并行优化的流水线结构。相位以角度为单位，输入输出位宽设置成16bit。

3.HDL代码设计及仿真验证

设计代码：
`timescale 1ns / 1ps

module cordic_ex#(parameter DIN_W = 16,
DOUT_W = 16)
(
input clk,
input [DIN_W-1:0] din,//2Q13
input din_vld,

output reg [DOUT_W+1-1:0] dout = 0,//2Q14
output reg dout_vld = 0
);

wire [DOUT_W*2-1 : 0] m_axis_dout_tdata;
wire m_axis_dout_tvalid;
wire signed [DOUT_W-1:0] sinh,cosh;

// ex = sinhx + coshx
always @(posedge clk)begin
dout end

assign sinh = m_axis_dout_tdata[DOUT_W*2-1 -:DOUT_W];
assign cosh = m_axis_dout_tdata[DOUT_W-1 -:DOUT_W];

always @(posedge clk)begin
if(m_axis_dout_tvalid)begin
dout_vld end
else
dout_vld end

cordic_0 cordic_cosh_sinh (
.aclk(clk), // input wire aclk
.s_axis_phase_tvalid(din_vld), // input wire s_axis_phase_tvalid
.s_axis_phase_tdata(din), // input wire [15 : 0] s_axis_phase_tdata
.m_axis_dout_tvalid(m_axis_dout_tvalid), // output wire m_axis_dout_tvalid
.m_axis_dout_tdata(m_axis_dout_tdata) // output wire [31 : 0] m_axis_dout_tdata
);

endmodule

cordic_ex

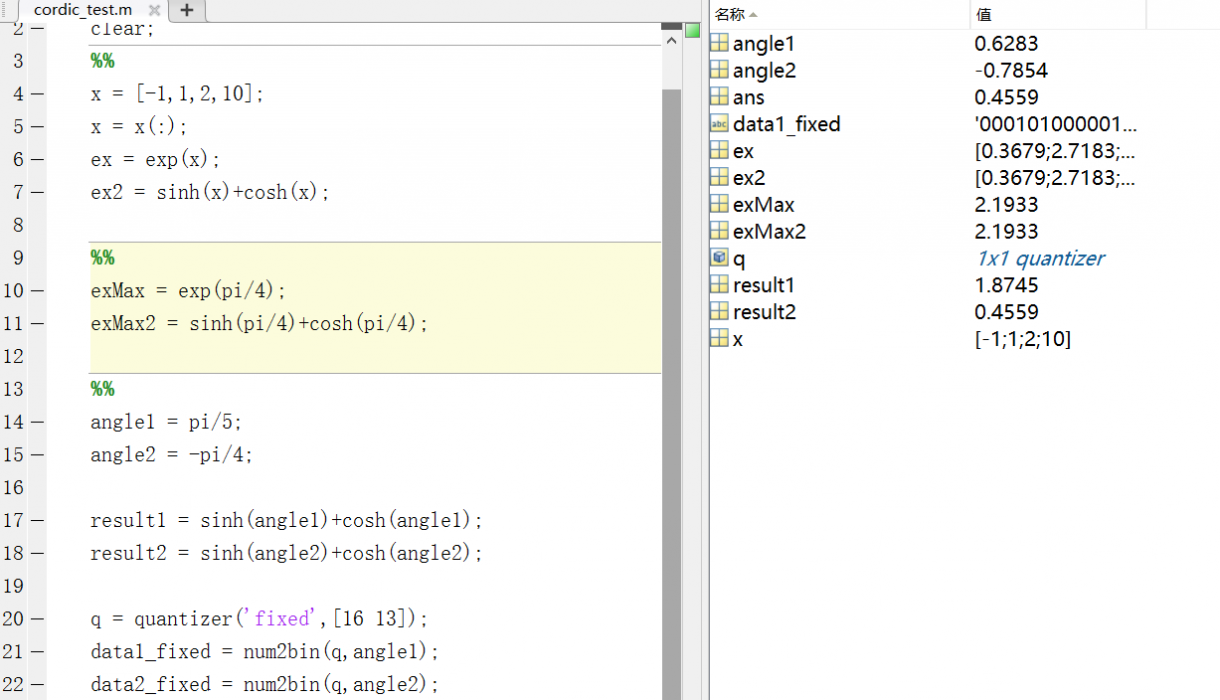
用MATLAB产生两组数据，并将角度值定点化后作为设计模块数据激励：

testbench：
`timescale 1ns / 1ps

module cordic_ex_tb();

parameter CYC = 20;

reg clk;
reg [16-1:0] din;
reg din_vld;

wire signed [17-1:0] dout;
wire dout_vld;

cordic_ex#(.DIN_W(16),
.DOUT_W(16))
uut(
.clk (clk) ,
.din (din) ,//2Q13
.din_vld (din_vld) ,
.dout (dout) ,//2Q14
.dout_vld (dout_vld)
);

initial begin
clk = 1;
forever #(CYC/2) clk = ~clk;
end

initial begin
#1;
din = 0;
din_vld = 0;
#(CYC*10);

din_vld = 1;
din = 16'b0001010000011011;//pi * 1/5
#(CYC*1);
din = 16'b1110011011011110;//-pi * 1/4
#5;
$stop;
end

endmodule

cordic_ex_tb

仿真结果：

仿真波形表明，计算结果与MATLAB浮点运算相近，满足一般计算需求。若想提高精度，可以增加CORDIC输出数据位宽。

参考文献：

1 ug479 7 Series DSP48E1 Slice User Guide.

2 Xilinx CORDIC算法(非常经典)_图文_百度文库 https://wenku.baidu.com/view/6c623aa8910ef12d2bf9e732.html

编辑：hfy