在之前的文章中,我们研究了信号x(t)的傅立叶变换的一些特性。总结一下:

考虑到傅里叶变换是可逆的,我们可以写成:
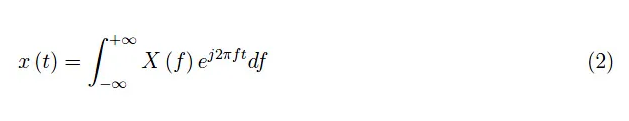
这个概念如图1所示。
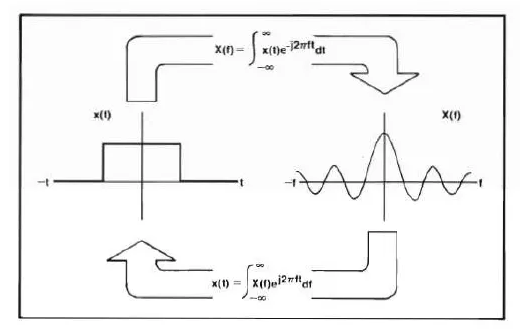
图1:傅里叶变换的反演运算
单位脉冲
让我们设想一个电路,它携带的电流在短时间内保持恒定值,然后消失。理想情况下,我们有:
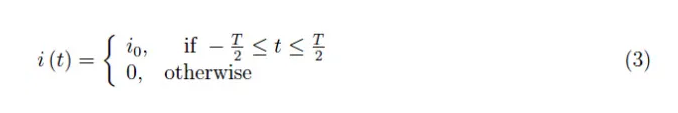
其中持续时间T足够小。此外,我们假设i0=Q0/T,其中Q0是与电流i0值相关的电荷(图2)。这个理想的实验使我们能够控制电流的持续时间T,同时保留电荷值。因此,通过减小T,我们得到如图3所示的趋势。
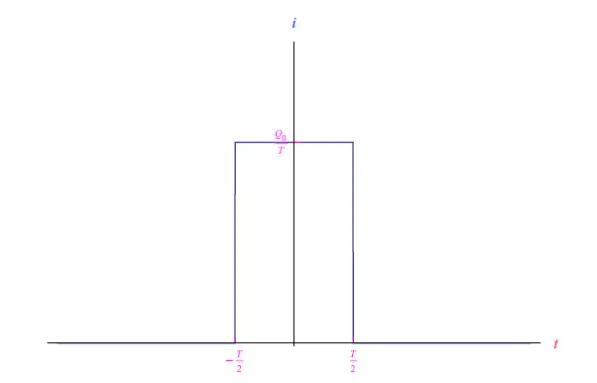
图2:方程(3)的电流趋势
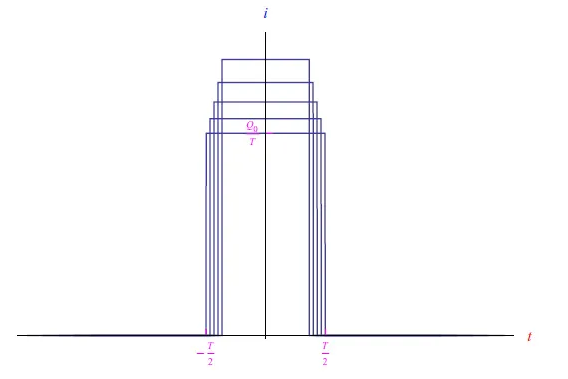
图3:持续时间T值减小的方程(3)的电流趋势。出于图形的原因,我们仅针对起始值突出显示i0/T
T的逐渐减小在数学上由极限通过运算表示:
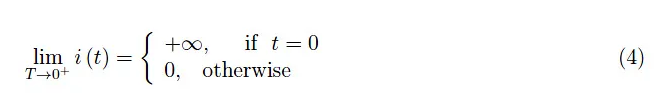
这显然是无稽之谈。然而,运算(4)中所涉及的电荷是Q0。事实上,电荷由下式给出:
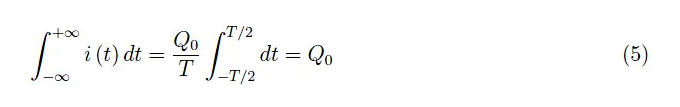
也就是说,图2中与T无关的矩形的面积:
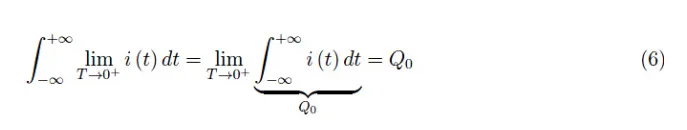
因此,“电流”(4)仍然与电荷Q0相关。由于(4)的模糊性,我们使用了引号。然而,结果(6)是显而易见的,因为“电流”尽管有一个无穷大的峰值,但持续时间却无穷小,并且我们知道0·∞也是无穷的形式,在这种情况下,它返回的是最终量Q0。用符号表示就是:

其中δ(t)是狄拉克δ函数:

式(6)涉及:
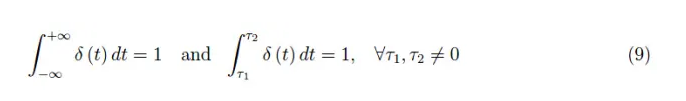
这一特性可概括为如下式子:

其中g(t)是任意正则函数。因此,积分值等于δ函数自变量消失时g(t)所假定的值。由此可见,对于一个平移的δ函数,我们有:
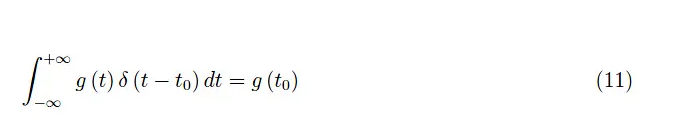
请注意,δ函数的量纲是其参数的倒数。因此,在我们的例子中,它具有时间的倒数(即频率)的量纲。
根据δ函数,电流(4)可以写成如下:

这就是所谓的单位脉冲或数学脉冲(图4)。
我们已经考虑了电流的具体情况,但也可以考虑电压。这里,单位脉冲可以写为v(t)=Aδ(t),其中A是一个常数,量纲为V·s。
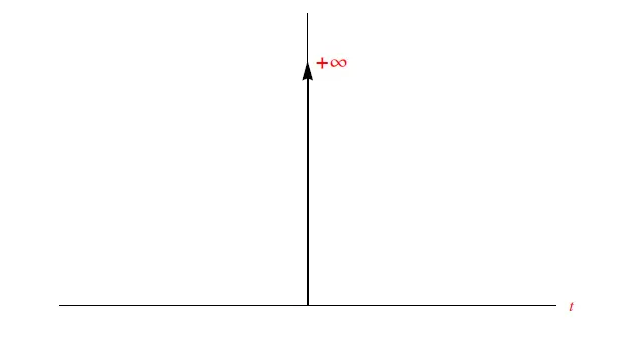
图4:单位脉冲的图形表示
傅里叶变换
任何单位脉冲在t=0处出现奇点都不会吓到我们,因为脉冲在任何情况下都会在无穷远处为零,因此我们预计傅里叶积分会收敛。事实上,对于特性(10),我们有:
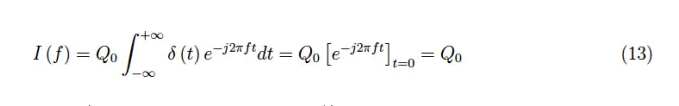
也就是说,单位脉冲的傅立叶频谱是平坦的。从物理上讲,这意味着单位脉冲可以分解为无数个从−∞到+∞的正弦频率振荡。
结论
为了定义单位脉冲,我们从矩形脉冲(3)开始,它在数学上更简单。从正弦振荡开始也能得到同样的结果,正弦振荡从−T/2处开始并在T/2处抵消。
我们建议读者证明傅里叶变换是一个“sinc”函数,即sin(f−f0)/(f−f0)类型,其中f0是截断振荡的频率。通过减少后者的持续时间,sinc函数“变宽”,在T→0的极限范围内变得严格平坦,从而再现了单位脉冲的傅里叶变换。相反,如果持续时间T逐渐增加,则sinc函数“收缩”,并且对于T→+∞为δ(f−f0),即以f0为中心的δ函数。这并不奇怪,因为我们现在有一个频率为f0的从−∞到+∞的完整振荡,因此傅里叶频谱是一条以f0为中心的线,在数学上用δ(f−f0)表示。
我们的结论是,必须牢记以下双重性:
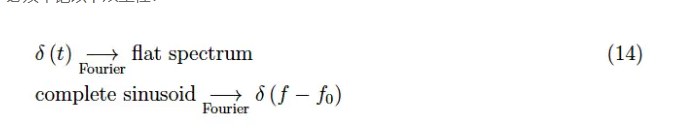
-
电流
+关注
关注
40文章
7192浏览量
140303 -
电荷
+关注
关注
1文章
663浏览量
37212 -
傅立叶变换
+关注
关注
3文章
105浏览量
33140
发布评论请先 登录
分贝单位的定义和应用
EE-70:ADSP-2106x SPORT DTx引脚:不同SHARC之间是否存在潜在的MCM数据争用






 单位脉冲的傅立叶变换是否存在?
单位脉冲的傅立叶变换是否存在?













评论