如何由傅里叶变换推出傅里叶反变换
傅里叶变换和傅里叶反变换是信号处理和通信领域中的两个重要概念,是数字信号和连续信号的重要数学分析方法之一。傅里叶变换可以将时间域信号转化为频率域信号,而傅里叶反变换则可以将频率域信号转化为时间域信号。本文将详细介绍如何由傅里叶变换推出傅里叶反变换。
一、傅里叶变换
傅里叶变换是一种将时间域信号表示为其频率分量的方法。其定义公式如下:
$$X(f)=\int_{-\infty}^{\infty}x(t)e^{-j2\pi ft}dt$$
其中,$x(t)$ 是时间域的信号,$X(f)$ 是频率域的信号,$f$ 是频率。该公式可以将信号 $x(t)$ 的频率分量 $X(f)$ 分解出来,可以得到信号在不同频率上的成分。
二、傅里叶反变换
傅里叶反变换是一种将频率域信号表示为其时间域成分的方法。其定义公式如下:
$$x(t)=\int_{-\infty}^{\infty}X(f)e^{j2\pi ft}df$$
其中,$x(t)$ 是时间域的信号,$X(f)$ 是频率域的信号,$f$ 是频率。该公式可以将频率域信号 $X(f)$ 解析成时间域信号 $x(t)$,可以得到信号在时间域上的成分。
三、如何由傅里叶变换推出傅里叶反变换
1. 推导傅里叶反变换的定义公式
我们先将傅里叶变换的定义公式进行变形,得到:
$$x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(f)e^{j2\pi ft}df$$
分析这个公式,可以看出它与傅里叶反变换的定义公式非常相似,只是多了一个系数 $\frac{1}{2\pi}$。因此,我们可以将傅里叶变换的定义公式中的 $X(f)$ 换成 $Y(f)$,得到:
$$y(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}Y(f)e^{j2\pi ft}df$$
这样就得到了傅里叶反变换的定义公式。
2. 推导傅里叶反变换的具体计算公式
上面的定义公式可以求出信号在时间域上的波形,但是并没有给出具体的计算方法。因此,我们需要推导傅里叶反变换的具体计算公式。
根据傅里叶变换的定义公式,可以得到:
$$X(f)=\int_{-\infty}^{\infty}x(t)e^{-j2\pi ft}dt$$
对该公式进行复数共轭操作,得到:
$$X^{*}(f)=\int_{-\infty}^{\infty}x^{*}(t)e^{j2\pi ft}dt$$
其中,$*$ 表示复数共轭。由于 $x(t)$ 是实函数,因此 $X^{*}(f)=X(-f)$。将其代入傅里叶反变换的定义公式中,得到:
$$y(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(-f)e^{j2\pi ft}df$$
对其进行变形,得到:
$$y(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(f)e^{-j2\pi ft}df$$
也就是傅里叶反变换的具体计算公式。
四、总结
本文详细介绍了如何由傅里叶变换推出傅里叶反变换。通过对傅里叶变换的定义公式进行复数共轭操作和代换,我们成功推导出了傅里叶反变换的定义公式和具体计算公式。由于傅里叶变换和傅里叶反变换是数字信号和连续信号的重要分析方法,对于信号处理和通信领域的研究具有非常重要的意义。
傅里叶变换和傅里叶反变换是信号处理和通信领域中的两个重要概念,是数字信号和连续信号的重要数学分析方法之一。傅里叶变换可以将时间域信号转化为频率域信号,而傅里叶反变换则可以将频率域信号转化为时间域信号。本文将详细介绍如何由傅里叶变换推出傅里叶反变换。
一、傅里叶变换
傅里叶变换是一种将时间域信号表示为其频率分量的方法。其定义公式如下:
$$X(f)=\int_{-\infty}^{\infty}x(t)e^{-j2\pi ft}dt$$
其中,$x(t)$ 是时间域的信号,$X(f)$ 是频率域的信号,$f$ 是频率。该公式可以将信号 $x(t)$ 的频率分量 $X(f)$ 分解出来,可以得到信号在不同频率上的成分。
二、傅里叶反变换
傅里叶反变换是一种将频率域信号表示为其时间域成分的方法。其定义公式如下:
$$x(t)=\int_{-\infty}^{\infty}X(f)e^{j2\pi ft}df$$
其中,$x(t)$ 是时间域的信号,$X(f)$ 是频率域的信号,$f$ 是频率。该公式可以将频率域信号 $X(f)$ 解析成时间域信号 $x(t)$,可以得到信号在时间域上的成分。
三、如何由傅里叶变换推出傅里叶反变换
1. 推导傅里叶反变换的定义公式
我们先将傅里叶变换的定义公式进行变形,得到:
$$x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(f)e^{j2\pi ft}df$$
分析这个公式,可以看出它与傅里叶反变换的定义公式非常相似,只是多了一个系数 $\frac{1}{2\pi}$。因此,我们可以将傅里叶变换的定义公式中的 $X(f)$ 换成 $Y(f)$,得到:
$$y(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}Y(f)e^{j2\pi ft}df$$
这样就得到了傅里叶反变换的定义公式。
2. 推导傅里叶反变换的具体计算公式
上面的定义公式可以求出信号在时间域上的波形,但是并没有给出具体的计算方法。因此,我们需要推导傅里叶反变换的具体计算公式。
根据傅里叶变换的定义公式,可以得到:
$$X(f)=\int_{-\infty}^{\infty}x(t)e^{-j2\pi ft}dt$$
对该公式进行复数共轭操作,得到:
$$X^{*}(f)=\int_{-\infty}^{\infty}x^{*}(t)e^{j2\pi ft}dt$$
其中,$*$ 表示复数共轭。由于 $x(t)$ 是实函数,因此 $X^{*}(f)=X(-f)$。将其代入傅里叶反变换的定义公式中,得到:
$$y(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(-f)e^{j2\pi ft}df$$
对其进行变形,得到:
$$y(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(f)e^{-j2\pi ft}df$$
也就是傅里叶反变换的具体计算公式。
四、总结
本文详细介绍了如何由傅里叶变换推出傅里叶反变换。通过对傅里叶变换的定义公式进行复数共轭操作和代换,我们成功推导出了傅里叶反变换的定义公式和具体计算公式。由于傅里叶变换和傅里叶反变换是数字信号和连续信号的重要分析方法,对于信号处理和通信领域的研究具有非常重要的意义。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
傅里叶变换
+关注
关注
6文章
444浏览量
43513
发布评论请先 登录
相关推荐
热点推荐
应用实例——如何解决双管反激变换器中的关断电压不均衡
反激变换器作为电源产品中几乎不可缺少的一个拓扑,从事电力电子产品开发的工程师是相当的熟悉,尤其是单管反激变换器,更是工程师从小白开始修炼的起点,万丈高楼平地起嘛。在经典的单管
数学-傅里叶级数的推导
本篇摘录“信号与系统3-傅里叶变换与频域分析”的小部分内容,作为正弦波生成的傅里叶级数展开法的补充。 1、矢量的正交分解 两矢量V1与V2正交,夹角为90°,那么两正交矢量的 内积为零
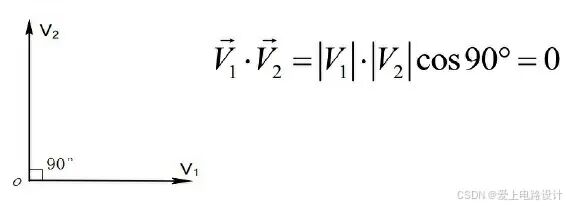
傅里叶变换的原理及应用
01什么是傅里叶变换?一句话概括:“把复杂信号拆成多个简单正弦波的叠加。”就像把一道混合光分解成彩虹(七色光),傅里叶变换能把任何波动信号(声音、图像、电磁波等)拆解成不同频率的“正弦波”组合。02

VirtualLab 应用:薄元近似(TEA)与傅里叶模态法(FMM)的光栅建模
(General Grating Component)允许用户在模拟中选择不同的求解算法。用户可以在严格的傅里叶模态法(FMM)和近似,但更快的薄元近似(TEA)之间进行选择。关于解算器的更多信息可以在这里找到
发表于 05-22 08:56
进群免费领FPGA学习资料!数字信号处理、傅里叶变换与FPGA开发等
进群免费领FPGA学习资料啦!小编整理了数字信号处理、傅里叶变换与FPGA开发等FPGA必看资料,需要的小伙伴可以加小助手(微信:elecfans123)或进 QQ 群:913501156 群免费领
发表于 04-07 16:41
VirtualLab Fusion应用:非近轴衍射分束器的设计与优化
地介绍了这一部分。
非近轴衍射分束器的严格分析
采用傅里叶模态法(FMM)对非近轴衍射分束器进行了严格的评价,该方法最初采用迭代傅里叶变换算法(IFTA)和薄元近似算法(TEA)进行
发表于 03-10 08:56
VirtualLab Fusion案例:高NA傅里叶单分子成像显微镜
1.摘要
傅里叶显微术广泛应用于单分子成像、表面等离子体观测、光子晶体成像等领域。它使直接观察空间频率分布成为可能。在高NA傅里
发表于 01-15 09:39
DFT与离散时间傅里叶变换的关系 DFT在无线通信中的应用
DFT与离散时间傅里叶变换(DTFT)的关系 DFT(离散傅里叶变换)与DTFT(离散时间傅里叶变换)都是信号处理中的重要工具,用于将信号从时域转换到频域。它们之间存在一定的联系和区别: 定义与对象
傅立叶变换在机器学习中的应用 常见傅立叶变换的误区解析
傅里叶变换在机器学习中的应用 傅里叶变换是一种将信号分解为其组成频率分量的数学运算,它在机器学习中的应用日益广泛。以下是一些主要的应用领域: 信号处理 : 音频处理:傅里叶变换有助于识别音频信号中
傅立叶变换与时域信号的关系 傅立叶变换在音频信号处理中的应用
傅里叶变换与时域信号的关系 傅里叶变换是一种数学工具,它能够将时域信号(即随时间变化的信号)转换为频域信号(即随频率变化的信号),或者将频域信号转换回时域信号。这种转换关系使得我们能够更加深入地理
傅立叶变换在图像处理中的作用
傅里叶变换在图像处理中发挥着至关重要的作用。以下是傅里叶变换在图像处理中的几个主要作用: 一、图像增强与去噪 去噪 :图像中的噪声通常表现为高频分量。通过傅里叶变换,可以将图像从空间域转换到频率域
傅立叶变换与拉普拉斯变换的区别
傅里叶变换与拉普拉斯变换在信号处理中都是非常重要的工具,但它们之间存在一些显著的区别。以下是对这两种变换区别的介绍: 定义域与适用范围 傅里叶变换 : 定义域:
傅立叶变换的基本概念 傅立叶变换在信号处理中的应用
傅里叶变换的基本概念 傅里叶变换是一种数学变换,它能够将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。这种变换在不同的研究领域有多种变体形式,如连





 如何由傅里叶变换推出傅里叶反变换
如何由傅里叶变换推出傅里叶反变换











评论