为什么有四种形式的傅里叶变换
傅里叶变换是一种十分重要的数学工具,它可以将函数从时域(即时间域)转换到频域,从而能够帮助人们更好地理解信号的特性。在傅里叶变换的研究过程中,出现了几种不同的变形方式,这其中包括了一维、二维、实数、离散四种形式,每种形式都有其独特的特点和适用场景。
一、一维傅里叶变换
一维傅里叶变换是最基础的傅里叶变换形式,它的变换公式如下:
$$ F(\omega) = \int_{-\infty}^{\infty}f(x)e^{-i\omega x}dx $$
其中,$f(x)$表示时域函数,$F(\omega)$表示频域函数,$\omega$表示频率。
此种变换主要适用于对一维信号的处理,如音频信号、振动信号等。经过一维傅里叶变换后,人们可以更加深入地分析信号的频域特性,从而能够对信号进行进一步的处理。
二、二维傅里叶变换
二维傅里叶变换是在一维傅里叶变换基础上发展而来的。它主要适用于处理二维信号,例如图像信号。
二维傅里叶变换的表达式如下:
$$ F(u,v) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)e^{-i(ux+vy)}dxdy $$
其中,$f(x,y)$表示二维信号(即图像),$F(u,v)$表示二维频域函数,$u$和$v$分别表示在$x$轴和$y$轴方向的频率。
二维傅里叶变换能够帮助人们更好地理解图像信号的频域特点,并且可以对图像进行一系列的处理,如图像增强、压缩等。
三、实数傅里叶变换
实数傅里叶变换是对傅里叶变换的一个特殊形式,它主要适用于实数信号处理。实数傅里叶变换的表达式如下:
$$ F_k=\sum_{n=0}^{N-1}f_n\cos\left(\frac{2\pi kn}{N}\right)-\sum_{n=0}^{N-1}f_ni\sin\left(\frac{2\pi kn}{N}\right) $$
其中,$f_n$为实数序列,$k$为频率,$N$为序列长度。需要注意的是,实数傅里叶变换得到的频域序列是对称的。
实数傅里叶变换的适用范围比较窄,但是在一些实际应用场景中,如声音信号处理、图像压缩等,常常需要使用实数傅里叶变换进行处理。
四、离散傅里叶变换
离散傅里叶变换是一种数字信号处理中最常用的傅里叶变换形式。它将时域信号转换为频域信号,并使用数字计算机进行处理。
离散傅里叶变换的表达式如下:
$$ X_k=\sum_{n=0}^{N-1}x_n e^{-i2\pi kn/N} $$
其中,$x_n$为时域离散信号,$X_k$为频域离散信号,$N$为序列长度。
离散傅里叶变换具有计算方便、速度快等优点,在数字信号处理中被广泛应用,如数据压缩、图像处理、视频压缩、声音处理等。
综上所述,傅里叶变换是十分重要的数学工具,能够帮助人们更好地理解信号的特性。通过不同形式的傅里叶变换,可以更好地处理不同类型的信号,例如一维信号、二维信号、实数信号和离散信号。对于傅里叶变换在数字化时代的应用,我们还需要不断探索和挖掘,为实际应用提供更好的支持。
傅里叶变换是一种十分重要的数学工具,它可以将函数从时域(即时间域)转换到频域,从而能够帮助人们更好地理解信号的特性。在傅里叶变换的研究过程中,出现了几种不同的变形方式,这其中包括了一维、二维、实数、离散四种形式,每种形式都有其独特的特点和适用场景。
一、一维傅里叶变换
一维傅里叶变换是最基础的傅里叶变换形式,它的变换公式如下:
$$ F(\omega) = \int_{-\infty}^{\infty}f(x)e^{-i\omega x}dx $$
其中,$f(x)$表示时域函数,$F(\omega)$表示频域函数,$\omega$表示频率。
此种变换主要适用于对一维信号的处理,如音频信号、振动信号等。经过一维傅里叶变换后,人们可以更加深入地分析信号的频域特性,从而能够对信号进行进一步的处理。
二、二维傅里叶变换
二维傅里叶变换是在一维傅里叶变换基础上发展而来的。它主要适用于处理二维信号,例如图像信号。
二维傅里叶变换的表达式如下:
$$ F(u,v) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)e^{-i(ux+vy)}dxdy $$
其中,$f(x,y)$表示二维信号(即图像),$F(u,v)$表示二维频域函数,$u$和$v$分别表示在$x$轴和$y$轴方向的频率。
二维傅里叶变换能够帮助人们更好地理解图像信号的频域特点,并且可以对图像进行一系列的处理,如图像增强、压缩等。
三、实数傅里叶变换
实数傅里叶变换是对傅里叶变换的一个特殊形式,它主要适用于实数信号处理。实数傅里叶变换的表达式如下:
$$ F_k=\sum_{n=0}^{N-1}f_n\cos\left(\frac{2\pi kn}{N}\right)-\sum_{n=0}^{N-1}f_ni\sin\left(\frac{2\pi kn}{N}\right) $$
其中,$f_n$为实数序列,$k$为频率,$N$为序列长度。需要注意的是,实数傅里叶变换得到的频域序列是对称的。
实数傅里叶变换的适用范围比较窄,但是在一些实际应用场景中,如声音信号处理、图像压缩等,常常需要使用实数傅里叶变换进行处理。
四、离散傅里叶变换
离散傅里叶变换是一种数字信号处理中最常用的傅里叶变换形式。它将时域信号转换为频域信号,并使用数字计算机进行处理。
离散傅里叶变换的表达式如下:
$$ X_k=\sum_{n=0}^{N-1}x_n e^{-i2\pi kn/N} $$
其中,$x_n$为时域离散信号,$X_k$为频域离散信号,$N$为序列长度。
离散傅里叶变换具有计算方便、速度快等优点,在数字信号处理中被广泛应用,如数据压缩、图像处理、视频压缩、声音处理等。
综上所述,傅里叶变换是十分重要的数学工具,能够帮助人们更好地理解信号的特性。通过不同形式的傅里叶变换,可以更好地处理不同类型的信号,例如一维信号、二维信号、实数信号和离散信号。对于傅里叶变换在数字化时代的应用,我们还需要不断探索和挖掘,为实际应用提供更好的支持。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
信号处理
+关注
关注
49文章
1094浏览量
104869 -
傅里叶变换
+关注
关注
6文章
444浏览量
43511
发布评论请先 登录
相关推荐
热点推荐
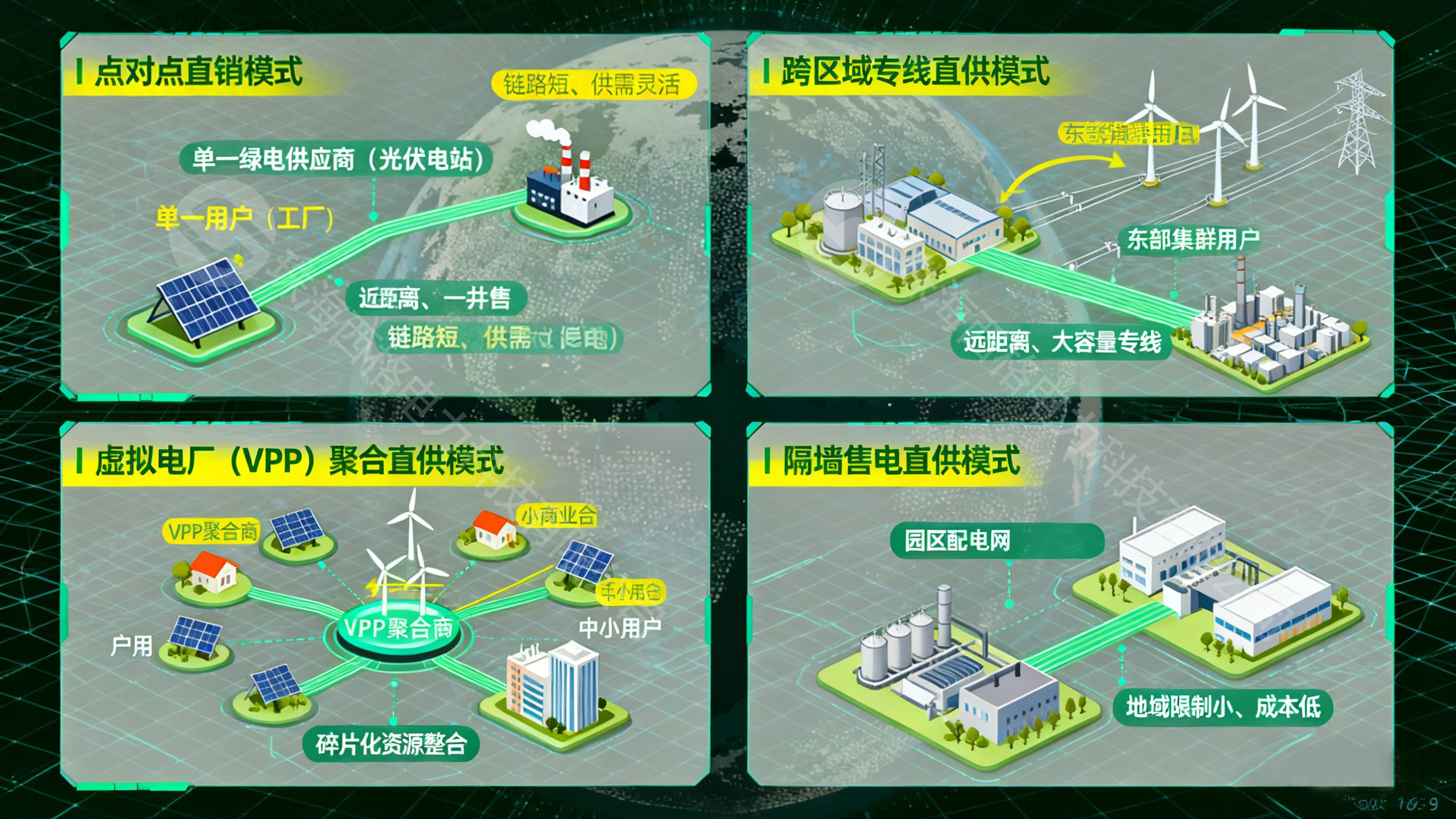
一图看懂绿电直连的四种玩法
通过 “总览框架 + 分模式图解” 的形式,用可视化逻辑拆解绿电直连的四种核心模式,涵盖每种模式的核心特征、适用场景、参与主体三大关键信息,帮你快速区分不同 “玩法” 的差异与适配性。
从入门到精通:基于开源代码的BLE四种模式开发详解
通过分析BLE低功耗蓝牙的四种核心工作模式,结合可下载、可修改的开放源码,本教程为开发者提供一套系统、实用的开发学习路径。 BLE(Bluetooth Low Energy): 也称为
傅里叶变换的原理及应用
01什么是傅里叶变换?一句话概括:“把复杂信号拆成多个简单正弦波的叠加。”就像把一道混合光分解成彩虹(七色光),傅里叶变换能把任何波动信号(声音、图像、电磁波等)拆解成不同频率的“正弦波”组合。02

RDMA简介3之四种子协议对比
RDMA协议共有四种子协议,分别为InfiniBand、iWARP、RoCE v1和RoCE v2协议。这四种协议使用统一的RDMA API,但在具体的网络层级实现上有所不同,如图1所示,接下来将
发表于 06-04 16:05
变频器主要支持哪四种模式?有什么区别?
变频器作为现代工业自动化领域中的关键设备,其控制模式的多样性和灵活性对于满足不同应用场景的需求至关重要。变频器主要支持四种控制模式:无PG的V/F模式、有PG的V/F模式、无PG的矢量控制模式以及有

芯片封装中的四种键合方式:技术演进与产业应用
自动键合和混合键合四种主流技术,它们在工艺流程、技术特点和应用场景上各具优势。本文将深入剖析这四种键合方式的技术原理、发展现状及未来趋势,为产业界提供技术参考。

进群免费领FPGA学习资料!数字信号处理、傅里叶变换与FPGA开发等
进群免费领FPGA学习资料啦!小编整理了数字信号处理、傅里叶变换与FPGA开发等FPGA必看资料,需要的小伙伴可以加小助手(微信:elecfans123)或进 QQ 群:913501156 群免费领
发表于 04-07 16:41
四种常见ADC的特性和应用
模拟-数字转换器(ADC)在现代电子系统中扮演着至关重要的角色,它们负责将连续的模拟信号转换为离散的数字信号。这一转换过程对于信号处理、通信、控制等多个领域都至关重要。本文将深入探讨四种常见的ADC
MSP430F4250的四种模式分别是在什么情况下使用呢?
我是一名初学者,看了书知道MSP430F4250的AD转换模式有四种,我想知道这四种转化模式有什么区别,分别应该在什么情况下使用。各位高手能否为我解答哈,在下不胜感激。因为是初学者,
发表于 01-06 06:16
私藏技术大公开!四种常见供电方案
在现代生活中,供电问题直接关系到我们的生活质量与工作效率。以下是四种超实用的供电方案,无论是在家庭生活还是工作场景中,都能为你提供稳定可靠的电力支持。 常见的物联网应用场景下,供电方式有四种
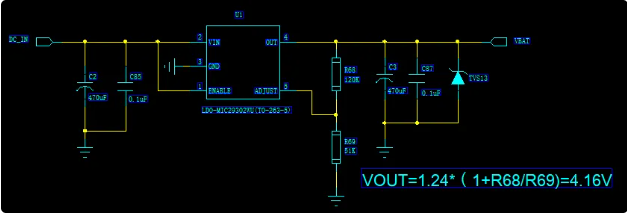
被问爆的四种供电方式,来啦~
4G模组的外部电源供电设计十分重要,对系统稳定、射频性能都有直接影响。 常见的物联网应用场景下,供电方式有四种: LDO供电方式 DCDC供电方式 锂电池供电以及充电方式 不可充电锂亚/锂锰电池供电

DFT与离散时间傅里叶变换的关系 DFT在无线通信中的应用
DFT与离散时间傅里叶变换(DTFT)的关系 DFT(离散傅里叶变换)与DTFT(离散时间傅里叶变换)都是信号处理中的重要工具,用于将信号从时域转换到频域。它们之间存在一定的联系和区别: 定义与对象
傅立叶变换在机器学习中的应用 常见傅立叶变换的误区解析
傅里叶变换在机器学习中的应用 傅里叶变换是一种将信号分解为其组成频率分量的数学运算,它在机器学习中的应用日益广泛。以下是一些主要的应用领域: 信号处理 : 音频处理:傅里叶变换有助于识
傅立叶变换与时域信号的关系 傅立叶变换在音频信号处理中的应用
傅里叶变换与时域信号的关系 傅里叶变换是一种数学工具,它能够将时域信号(即随时间变化的信号)转换为频域信号(即随频率变化的信号),或者将频域信号转换回时域信号。这种转换关系使得我们能够更加深入地理
傅立叶变换的基本概念 傅立叶变换在信号处理中的应用
傅里叶变换的基本概念 傅里叶变换是一种数学变换,它能够将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。这种变换





 为什么有四种形式的傅里叶变换
为什么有四种形式的傅里叶变换











评论