拉普拉斯变换的意义
拉普拉斯变换是微积分中的一种重要方法,用于将时间域函数转换为复平面的频域函数。它是工程和科学中常用的一种数学工具,尤其是电路理论、信号处理和控制理论中。
拉普拉斯变换的意义可以从下面四个方面来阐述:
一、用于描述电路系统的行为
在电路理论中,我们经常需要描述电路的行为,如电压、电流等的变化情况,利用拉普拉斯变换可以将电路中的时域信号转换为复频域信号,方便我们进行分析和计算。
利用拉普拉斯变换的性质,可以将电路中的微分方程或积分方程转换为代数方程。这种转换为求解电路的稳态或暂态问题提供了更为方便的方法。
例如,对于一个简单的电路,其电压与时间的关系可以表示为V(t),如果我们将其进行拉普拉斯变换,得到复频域函数V(s)。这样,我们就可以通过对V(s)进行分析,了解电路在频域中的行为,获得更加全面的信息。
二、用于信号处理
信号处理是指将信号进行变换或处理,获取信号的有用信息的过程。在信号处理中,我们常常需要对信号进行滤波、降噪、压缩等处理。利用拉普拉斯变换,我们可以将信号由时域转换为复频域,便于我们对信号进行处理和分析。
例如,将一个幅度为A、频率为f的正弦波S(t)=Asin(2πft)进行拉普拉斯变换,得到复频域函数S(s)=A/(s+j2πf)。这样,我们就可以通过对S(s)进行分析来进行滤波处理。
三、用于控制理论
控制理论在许多领域中都有应用,如机械、化工、航空等领域。在控制理论中,我们需要对系统的传递函数进行分析和设计。利用拉普拉斯变换,可以方便地对系统进行建模和分析,对系统进行控制。
例如,我们可以将系统的微分方程表示为x''(t)+2ξωnx'(t)+ωn^2x(t)=F(t),其中ξ和ωn分别为系统的阻尼比和固有频率。将其进行拉普拉斯变换,得到X(s)=[F(s)+sx(0)+x'(0)]/[(s^2)+2ξωns+sωn^2]。这样,我们就可以通过对X(s)的分析来设计系统的传递函数,并进行控制。
四、用于微积分研究
拉普拉斯变换可以用于微积分研究中,如傅里叶变换、广义函数等的研究。其中,傅里叶变换可以看作是拉普拉斯变换的特例,当拉普拉斯变换的实部s为无穷大时,便得到了傅里叶变换。
广义函数(或称狄拉克函数)是一种函数,其积分在某些情况下得到的结果是0,但在某些情况下却得到了非零结果。广义函数与拉普拉斯变换之间存在着密切的关系。通过拉普拉斯变换,我们可以更好地理解广义函数在微积分研究中的作用和意义。
总之,拉普拉斯变换在工程和科学中的应用非常广泛,可以帮助我们更好地理解和分析各种系统、信号和函数的特性,为工程和科学的发展提供了强有力的数学支撑。
拉普拉斯变换是微积分中的一种重要方法,用于将时间域函数转换为复平面的频域函数。它是工程和科学中常用的一种数学工具,尤其是电路理论、信号处理和控制理论中。
拉普拉斯变换的意义可以从下面四个方面来阐述:
一、用于描述电路系统的行为
在电路理论中,我们经常需要描述电路的行为,如电压、电流等的变化情况,利用拉普拉斯变换可以将电路中的时域信号转换为复频域信号,方便我们进行分析和计算。
利用拉普拉斯变换的性质,可以将电路中的微分方程或积分方程转换为代数方程。这种转换为求解电路的稳态或暂态问题提供了更为方便的方法。
例如,对于一个简单的电路,其电压与时间的关系可以表示为V(t),如果我们将其进行拉普拉斯变换,得到复频域函数V(s)。这样,我们就可以通过对V(s)进行分析,了解电路在频域中的行为,获得更加全面的信息。
二、用于信号处理
信号处理是指将信号进行变换或处理,获取信号的有用信息的过程。在信号处理中,我们常常需要对信号进行滤波、降噪、压缩等处理。利用拉普拉斯变换,我们可以将信号由时域转换为复频域,便于我们对信号进行处理和分析。
例如,将一个幅度为A、频率为f的正弦波S(t)=Asin(2πft)进行拉普拉斯变换,得到复频域函数S(s)=A/(s+j2πf)。这样,我们就可以通过对S(s)进行分析来进行滤波处理。
三、用于控制理论
控制理论在许多领域中都有应用,如机械、化工、航空等领域。在控制理论中,我们需要对系统的传递函数进行分析和设计。利用拉普拉斯变换,可以方便地对系统进行建模和分析,对系统进行控制。
例如,我们可以将系统的微分方程表示为x''(t)+2ξωnx'(t)+ωn^2x(t)=F(t),其中ξ和ωn分别为系统的阻尼比和固有频率。将其进行拉普拉斯变换,得到X(s)=[F(s)+sx(0)+x'(0)]/[(s^2)+2ξωns+sωn^2]。这样,我们就可以通过对X(s)的分析来设计系统的传递函数,并进行控制。
四、用于微积分研究
拉普拉斯变换可以用于微积分研究中,如傅里叶变换、广义函数等的研究。其中,傅里叶变换可以看作是拉普拉斯变换的特例,当拉普拉斯变换的实部s为无穷大时,便得到了傅里叶变换。
广义函数(或称狄拉克函数)是一种函数,其积分在某些情况下得到的结果是0,但在某些情况下却得到了非零结果。广义函数与拉普拉斯变换之间存在着密切的关系。通过拉普拉斯变换,我们可以更好地理解广义函数在微积分研究中的作用和意义。
总之,拉普拉斯变换在工程和科学中的应用非常广泛,可以帮助我们更好地理解和分析各种系统、信号和函数的特性,为工程和科学的发展提供了强有力的数学支撑。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
信号处理器
+关注
关注
1文章
262浏览量
26111 -
拉普拉斯变换
+关注
关注
1文章
32浏览量
10448
发布评论请先 登录
相关推荐
热点推荐
Cypress赛普拉斯FRAM增强车载黑匣子EDR抗干扰能力
Cypress赛普拉斯512Kbit FRAM凭借微秒级写入、10^14次擦写寿命及151年数据保留,为车载黑匣子EDR提供高可靠数据存储。其-40℃~105℃车规级工作范围确保碰撞数据完整记录,满足汽车安全法规严苛要求。

罗彻斯特电子对HOTlink®和 HOTLINK II™的持续支持
长期可靠的解决方案 2023年,英飞凌(Infineon)发布了HOTLink和HOTLink II产品的停产通知,同时宣布了与罗彻斯特电子就该产品线的独家合作,旨在确保赛普拉斯(Cypress
信号处理简介:移动平均滤波器
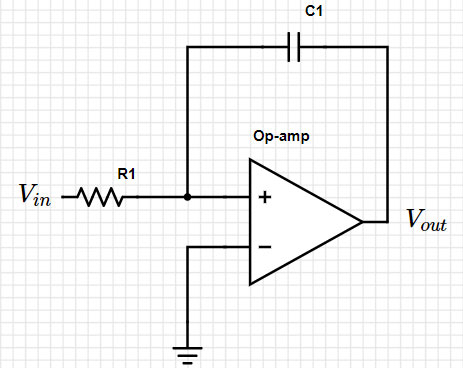
设计电路,以任何我们想要的方式控制信号。我们竟然能够使用电阻器、电容器和运算放大器 (op-amps) 等电子元器件组合来模拟积分和微分等数学工具,这着实令人惊叹。 例如以下电路(图1): 图 1:简单的积分电路。(图片来源:Mustahsin Zarif) 进入拉普拉斯
赛普拉斯FRAM宽温域生命守护
赛普拉斯2 Mbit FRAM FM25V20A-DG以40 MHz SPI总线、10¹²次擦写寿命和100 krad(Si)抗辐射能力,取代呼吸机中EEPROM与SRAM加电池的传统方案,为智能生命支持系统提供原子级可靠的数据存储基石。

CYPD7191-40LDXS 是否同时支持 Miniprog3 和 Miniprog4?
CYPD7191-40LDXS? 它似乎无法选择CYPD7191-40LDXS 器件。
Q3) 还是可以使用赛普拉斯编程器选择器件?
Q4)是否使用 ModusToolBox 为 CYPD7191-40LDXS 开发 FW?
Q5)是否有任何与上述 CCG7S 有关的计划编制材料?
请回答每个问题(Q1 ~ Q5
发表于 05-23 06:09
USB CYPRESS 3014芯片无法正常启动怎么解决?
你好,我们使用的是具有 USB 启动模式的赛普拉斯 3014 USB 芯片。 我的电脑可以在设备管理器中检测到 3014,但 USB 芯片无法与板上的 FPGA 通信。 电源电压似乎正常。 3014
发表于 05-20 07:09
2.0 USB集线器CYUSB2304-68LTXI在重新枚举全速设备时出现错误怎么解决?
运行 ubuntu 23.10。
在赛普拉斯评估板CY4603上(请注意,这是一个 3.0 集线器,但来自同一系列)我没有收到这些错误。
我觉得奇怪的是,我在使用评估板时没有遇到这个错误。 我是否在集线器上连接了错误的东西?这是一个已知问题吗?有没有什么解决办法?
发表于 05-19 07:32
如何将CYUSB2014与传感器AR0144CS连接起来?
我们正在尝试将 CYUSB2014 与传感器 AR0144CS 连接起来。
我参考了AN65974来实现从属fifo接口通信。
在这里,我的疑问是,由于它是一个传感器接口,赛普拉斯 FX3 应该充当
发表于 05-19 06:11
马达控制上必要的知识 三角函数
) 控制理论:普拉普斯变换,传递函数,古典控制(比例积分控制),滤波器
本技术资料说明的是:三角函数。*附件:马达控制上必要的知识 三角函数.pdf
发表于 03-18 12:23
信号与系统 MIT
信号与系统的主要内容有:线性时不变系统,周期信号的傅里叶级数表示,连线时间傅里叶级变换 ,离散时间傅里叶级变换,信号与系统的时域和频域特性,采样,通信系统,拉普拉斯变换,Z
发表于 02-27 19:17
DLP3010 GUI无法与dlpc通信怎么解决?
我利用DLP3010evm的displayboard和自己做的一块底板连接。
去除了底板上的MSP430,直接将赛普拉斯芯片与dlpc连接。赛普拉斯芯片配置和evm一样。
可以烧录固件,但是GUI
发表于 02-27 08:07
罗彻斯特电子拓宽与ISSI的合作,扩展产品可用性
在过去的二十年中,SRAM存储器市场发生了巨大变化;技术进步使得许多分立的SRAM被更高性价比的集成方案所取代。诸如赛普拉斯(Cypress)、GSI、瑞萨(Renesas)和三星(Samsung
傅立叶变换与拉普拉斯变换的区别
傅里叶变换与拉普拉斯变换在信号处理中都是非常重要的工具,但它们之间存在一些显著的区别。以下是对这两种变换区别的介绍: 定义域与适用范围 傅里叶变换





 拉普拉斯变换的意义
拉普拉斯变换的意义












评论