傅里叶变换和系统的频域分析(1)

傅里叶变换和系统的频域分析

Mother's Day

信号分解为正交函数

信号分解为正交函数的原理与矢量分解为正交矢量的概念相似。譬如，在平面上的矢量A在直角坐标系中可以分解为x方向分量和y方向分量。

例:令v,m分别是x轴和y轴的单位矢量，则矢量A可表示为C1 v +C2 m (C1,C2为常数)
因此空间矢量正交分解的概念可以推广到信号空间，在信号空间找到若干个相互正交的信号作为基本信号，使得信号空间中任一信号均可以表示成他们的线性组合。

一、正交函数集

1、正交: 如有定义在(t1,t2)区间的两个函数φ1(t)和φ2(t)，若满足

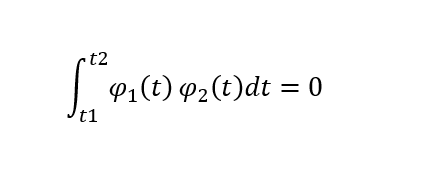
则称φ1(t)和φ2(t)在区间(t1,t2)内正交。

2、正交函数集： 如有n个函数φ1(t),φ2(t),...,φn(t)构成一个函数集，当这些函数在区间(t1,t2)内满足

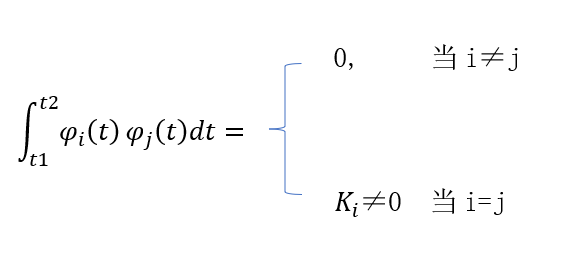
式中Ki为常数，则称此函数集为在区间(t1,t2)的正交函数集。

3、完备正交函数集：

4、三角函数集：

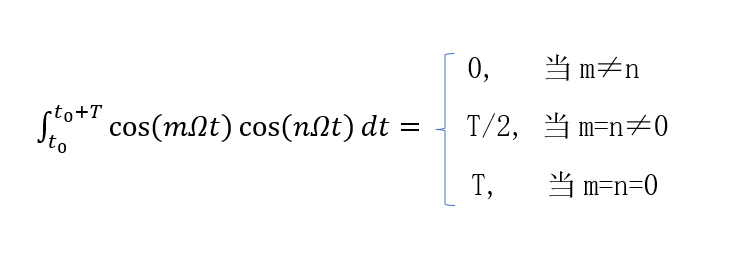
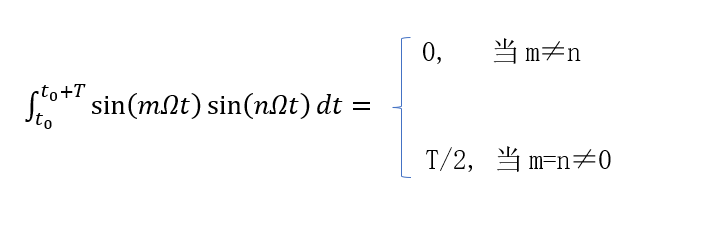
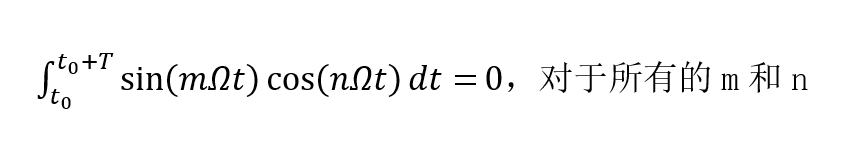
5、复函数集：

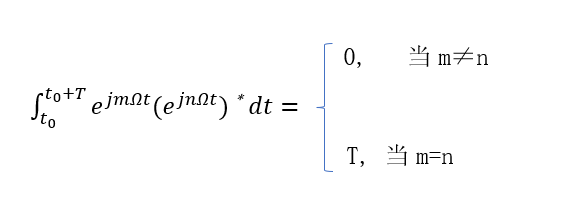
二、信号分解为正交函数