在机器学习(ML)中,最重要的线性代数概念之一是奇异值分解(SVD)和主成分分析(PCA)。在收集到所有原始数据后,我们如何发现其中的结构?例如,通过过去6天的利率,我们能否理解其组成并发现趋势?

对于高维原始数据,这变得更加困难,就像在一堆干草中找针一样。SVD使我们能够提取和解开信息。在本文中,我们将详细介绍SVD和PCA。我们假设您具备基本的线性代数知识,包括秩和特征向量。如果您在阅读本文时遇到困难,我建议您先刷新这些概念。在本文末尾,我们将回答上面的利率示例中的一些问题。本文还包含可选部分。根据您的兴趣程度随意跳过。
误解
我发现一些非初学者可能会问这样的问题。PCA是降维吗?PCA确实可以降维,但它远远不止于此。我喜欢维基百科的描述:
主成分分析(PCA)是一种统计过程,它使用正交变换将一组可能存在相关性的变量(每个实体都具有各种数值)的观测值转换为一组线性不相关变量的值,这些变量称为主成分。
从一个简化的角度来看,PCA将数据线性转换为彼此不相关的新属性。对于机器学习而言,将PCA定位为特征提取,可能比将其定位为降维更能充分发挥其潜力。
SVD和PCA的区别是什么?SVD将矩阵对角化为易于操作和分析的特殊矩阵,从而为将数据分解成独立成分奠定了基础。PCA跳过了较不重要的成分。显然,我们可以使用SVD来找到PCA,方法是在原始SVD矩阵中截断较不重要的基向量。
矩阵对角化
在特征值和特征向量的文章中,我们描述了一种将n×n方阵A分解为以下形式的方法:
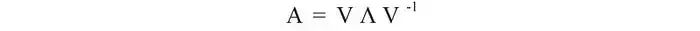
例如,
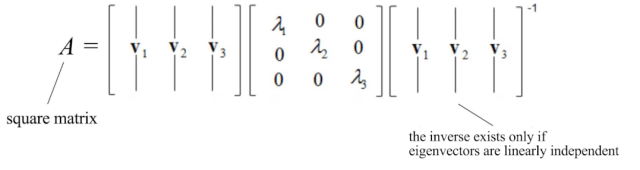
如果A是一个方阵并且A具有n个线性无关的特征向量,则可以将矩阵对角化。现在,是时候使用SVD为所有矩阵开发解决方案了。
奇异向量和奇异值
在线性代数中,矩阵AAᵀ和AᵀA非常特殊。考虑任何m×n矩阵A,我们可以分别将其与Aᵀ相乘以形成AAᵀ和AᵀA。这些矩阵:
- 对称的,
- 方阵,
- 至少是半正定的(特征值为零或正),
- 这两个矩阵具有相同的正特征值,
- 这两个矩阵的秩与A的秩相同,均为r。
此外,我们在机器学习中经常使用的协方差矩阵也处于这种形式。由于它们是对称的,我们可以选择其特征向量为正交的(彼此垂直且长度为1)——这是对称矩阵的基本性质。

现在,让我们介绍一些在SVD中经常使用的术语。我们在这里将AAᵀ的特征向量称为uᵢ,将AᵀA的特征向量称为vᵢ,并将这些特征向量集合u和v称为A的奇异向量。这两个矩阵具有相同的正特征值。这些特征值的平方根被称为奇异值。
到目前为止还没有太多解释,但让我们先把所有东西放在一起,解释将在接下来给出。我们将向量uᵢ连接成U,将向量vᵢ连接成V,以形成正交矩阵。
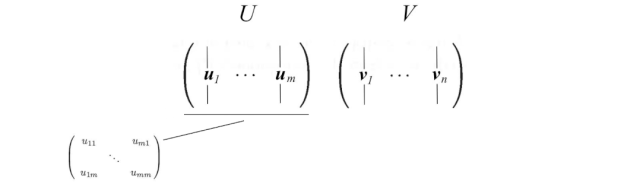
由于这些向量是正交的,很容易证明U和V遵循以下关系:
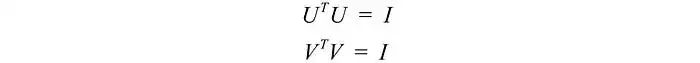
SVD
我们先从难的部分开始。SVD表明,任何矩阵A都可以分解为:
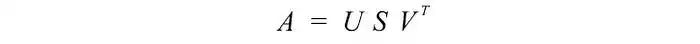
其中U和V是正交矩阵,其特征向量分别从AAᵀ和AᵀA中选择。S是一个对角矩阵,其r个元素等于AAᵀ或AᵀA的正特征值的平方根(这两个矩阵具有相同的正特征值)。对角线元素由奇异值组成。
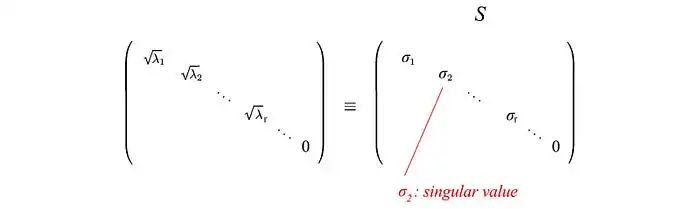
即一个m×n矩阵可以分解为:
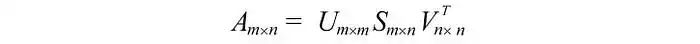
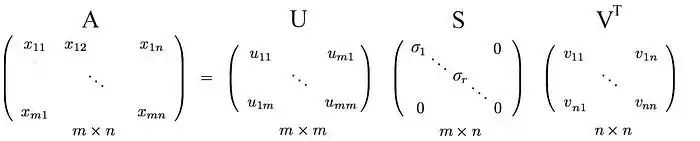
我们可以按不同的顺序排列特征向量来产生U和V。为了标准化解决方案,我们将特征值较大的向量排在较小的值的前面。
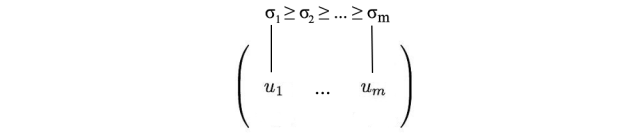
与特征值分解相比,SVD适用于非方阵。对于SVD中的任何矩阵,U和V都是可逆的,并且它们是正交的,这是我们所喜欢的。在这里不提供证明,我们还告诉您,奇异值比特征值更具数值稳定性。
示例
在进一步深入之前,让我们用一个简单的例子来演示一下。这将使事情变得非常容易理解。
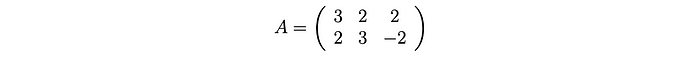
计算:
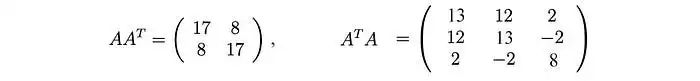
这些矩阵至少是半正定的(所有特征值均为正或零)。如图所示,它们共享相同的正特征值(25和9)。下面的图还显示了它们对应的特征向量。
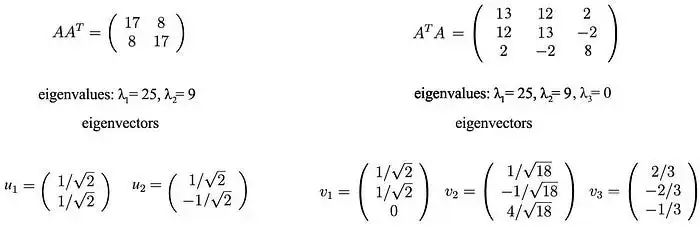
奇异值是正特征值的平方根,即5和3。因此,SVD分解为:
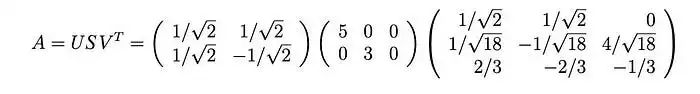
证明(可选)
为了证明SVD,我们要解出U、S和V,使得:
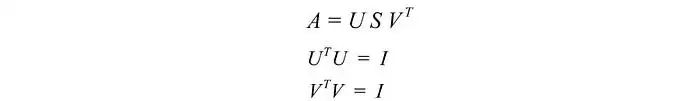
我们有三个未知数。希望我们可以使用上面的三个方程解决它们。A的转置为:
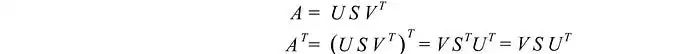
已知
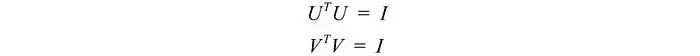
计算 AᵀA,
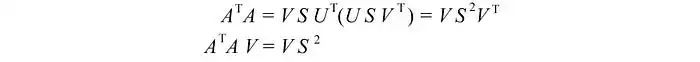
最后一个方程相当于矩阵(AᵀA)的特征向量定义。我们只是将所有特征向量放入一个矩阵中。

其中VS²等于
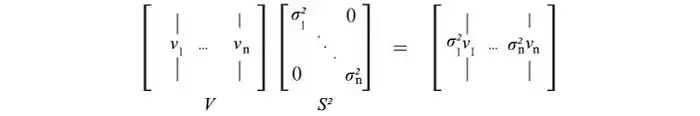
V保存AᵀA的所有特征向量vᵢ,而S保存AᵀA的所有特征值的平方根。我们可以对AAᵀ重复相同的过程,并得到类似的方程式。
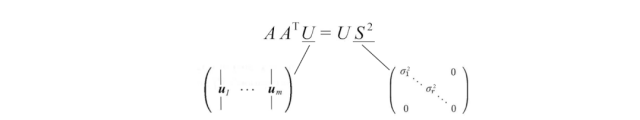
现在,我们只需要解出U、V和S,使其符合以下条件:
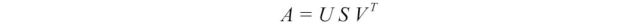
总结
以下是SVD的总结。
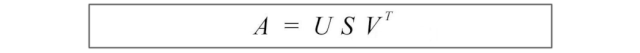
其中
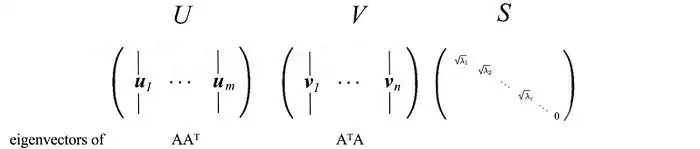
重新表述SVD
由于矩阵V是正交的,VᵀV等于I。我们可以将SVD方程重写为:
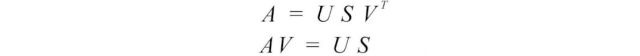
这个方程式建立了uᵢ和vᵢ之间的重要关系。
回顾

应用AV = US,
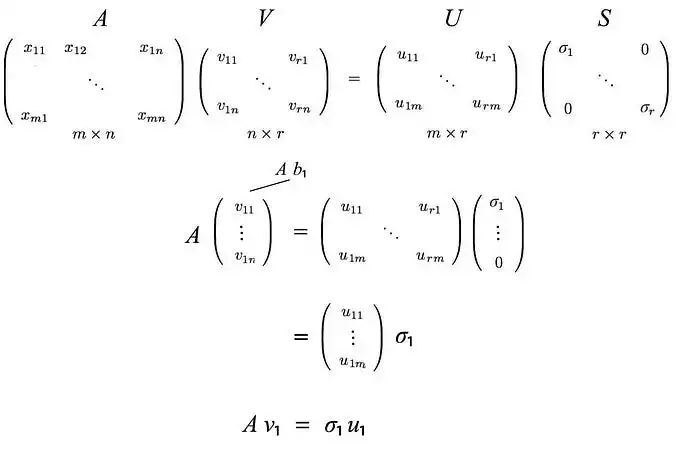
这可以推广为:

回顾
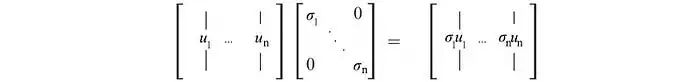
and
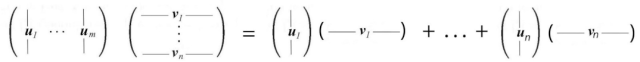
SVD分解可以被认为是uᵢ和vᵢ的一系列外积。
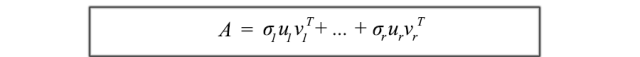
这种SVD的公式化是理解A的构成要素的关键。它提供了一种将纠缠在一起的m×n数据数组分解为r个组件的重要方法。由于uᵢ和vᵢ是单位向量,我们甚至可以忽略具有非常小奇异值σᵢ的项(σᵢuᵢvᵢᵀ)。 (稍后我们会回到这个问题。)
让我们先重用之前的例子,展示一下它是如何工作的。
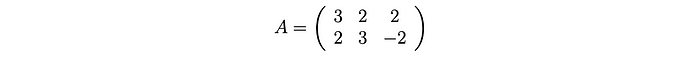
上面的矩阵A可以分解为:
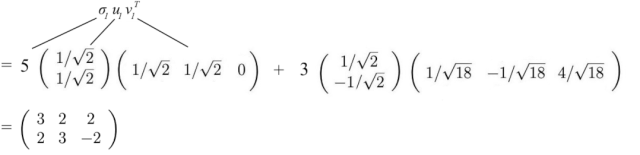
列空间,行空间,左零空间和零空间(可选-高级用户)
接下来,我们将看看U和V由什么组成。假设A是一个秩为r的m×n矩阵。AᵀA将是一个n×n的对称矩阵。所有对称矩阵都可以选择n个正交的特征向量vⱼ。由于Avᵢ = σᵢuᵢ,而vⱼ是AᵀA的正交特征向量,我们可以计算uᵢᵀuⱼ的值:
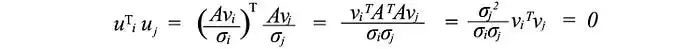
它等于零,即uᵢ和uⱼ互相正交。如前所述,它们也是AAᵀ的特征向量。
由于Avᵢ = σuᵢ,我们可以认识到uᵢ是A的列向量。

由于A的秩为r,所以我们可以选择这r个uᵢ向量为正交基。那么AAᵀ的剩余m-r个正交特征向量是什么呢?由于A的左零空间与列空间正交,因此将其选为剩余的特征向量非常自然。(左零空间N(Aᵀ)是由Aᵀx = 0定义的空间。)对于AᵀA的特征向量,类似的论证也是适用的。因此,我们有:

从前面的SVD方程式回到原来的方程式,我们有:
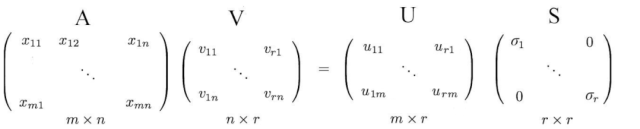
我们只需将特征向量放回左零空间和零空间中。
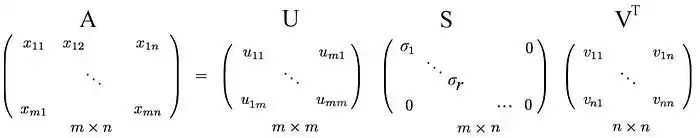
Moore-Penrose伪逆
对于线性方程组,我们可以计算一个方阵A的逆来求解x。
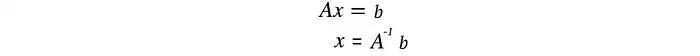
但并非所有矩阵都可逆。而且,在机器学习中,由于数据中存在噪声,很难找到精确的解。我们的目标是找到最适合数据的模型。为了找到最佳拟合解,我们需要计算一个伪逆。
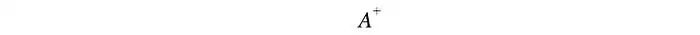
该伪逆最小化以下最小二乘误差:

解x的估计值为:
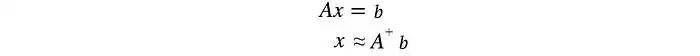
在线性回归问题中,x是我们的线性模型,A包含训练数据,b包含相应的标签。我们可以通过以下方式解决x:
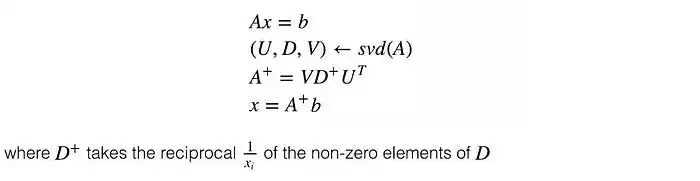
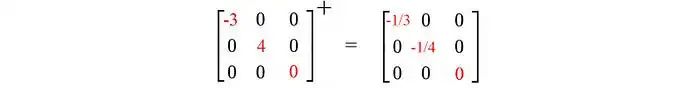
下面是一个例子

方差和协方差
在机器学习中,我们识别模式和关系。我们如何确定数据中属性之间的相关性?让我们从一个例子开始讨论。我们随机抽取了12个人的身高和体重,并计算它们的均值。我们通过将原始值减去其均值来将其零中心化。例如,下面的矩阵A保存了调整后的零中心化身高和体重。
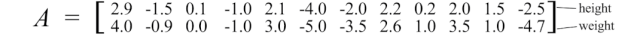
当我们绘制数据点时,我们可以看出身高和体重是正相关的。但是我们如何量化这种关系呢?
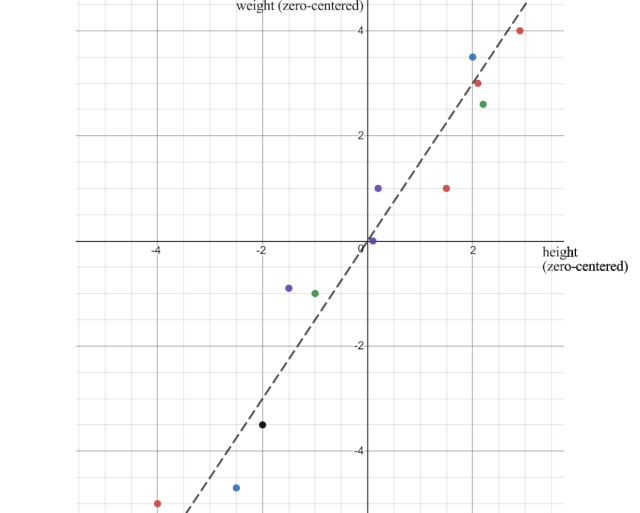
首先,一个属性如何变化?我们可能在高中就学过方差。让我们介绍一下它的近亲。样本方差的定义为:
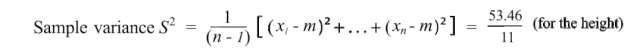
注意,它的分母为n-1而不是n。由于样本数量有限,样本均值存在偏差并与样本相关。相对于总体,平均平方距离会更小。样本协方差S²除以n-1来抵消这个偏差,可以被证明是方差σ²的无偏估计。
-
ML
+关注
关注
0文章
154浏览量
35390 -
SVD
+关注
关注
0文章
21浏览量
12410 -
机器学习
+关注
关注
66文章
8541浏览量
136227
发布评论请先 登录
基于改进奇异值分解的人耳识别算法研究
采用奇异值分解的数字水印嵌入算法
《工程线性代数(MATLAB版)》程序集
基于整体与部分奇异值分解的人脸识别
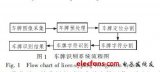
基于奇异值分解的车牌特征提取方法研究
机器学习进阶之线性代数-奇异值分解(下)
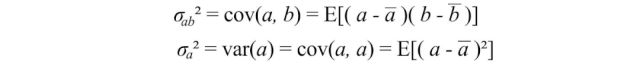





 机器学习进阶之线性代数-奇异值分解(上)
机器学习进阶之线性代数-奇异值分解(上)












评论