最近进行代码的review过程中看到同事在代码中直接拿浮点数相等来作为条件,其他同事提醒他的时候,他还迷迷糊糊不知道为什么,所以就有了今天这篇文章。
1、浮点数据的不均匀
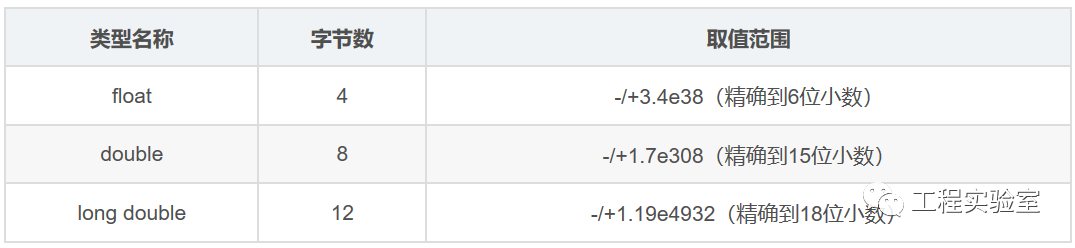
我们经常会谈到浮点数的精度问题,float-单精度,double-双精度,double类型相比float类型精度更高,相应的需要的内存字节个数也越多,谈到精度的问题,其实也就说明这种数据类型并不能够连续的标识任何的点,整形数就不用说了,小数部分直接不能标识。
毒王这篇文章基本上可以从浮点数的存储到表意来较好的认识浮点数数据类型,但是中间部分对于浮点数精度部分的介绍并不是很形象,所以今天再详细一点说明一下。
首先我们要认识到通常float类型的变量占据四个字节,而uint32_t的整形类型也是占据四个字节,既然都是四个字节,那他们所能表示的不同数据个数是一样的。
如果不太理解,可以把float看成4个bit,uint32_t也是4个bit,那么他们不管经过什么变换,每个数据类型都只能够标识16个数。
好,如下图以4字节float的数据存储模型所示:

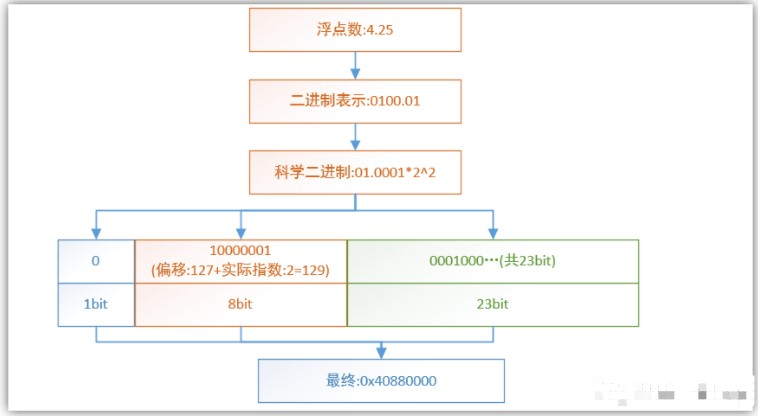
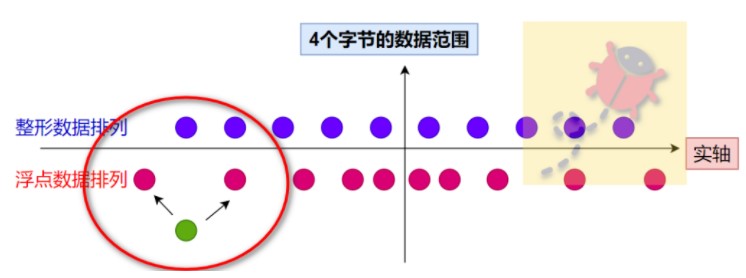
4个字节的浮点数,不像无符号整形所有的bit都是数据区,并且以每个数据之间相差1均匀分布,而浮点数把这4个字节分为了不同的区来起到不同的作用,从而用另外一种方式表达数据。
其指数部分越大,表示的数据就越大,但是尾数部分只能表示到23位,这样的话导致数据的精度就越差,如果不太理解可以用一个较大的数通过上面的转换方式进行换算,便能理解。
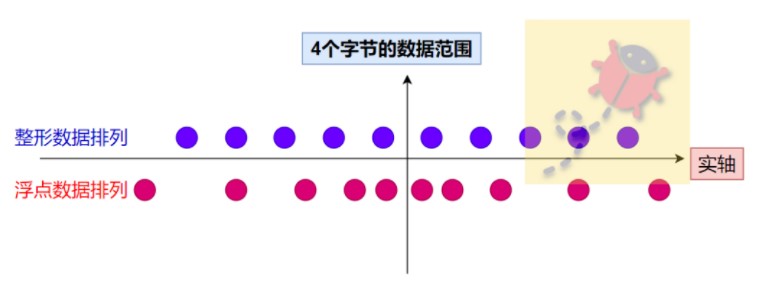
所以同样是4个字节,根据浮点数的表示,越接近0就越稠密,越远离0就越稀疏,呈现一种不均匀的数据排列状态,如上图所示,同样它也也不能标识实轴上任意的点。
2、验证一下不均匀
好了,讲了这么多理论,多多少少得来点程序验证一下:
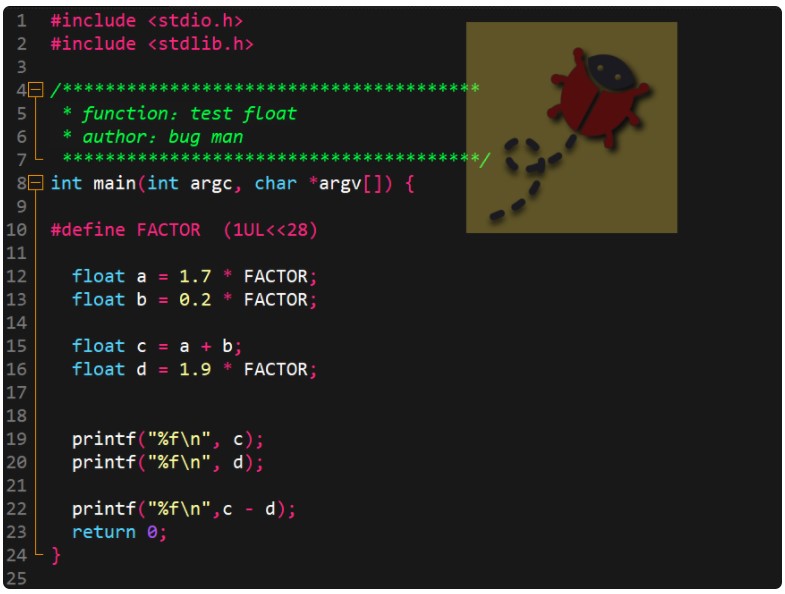
看看上面的代码,这还用说,肯定这两个数相等呀,相减也等于0,然而看一下输出结果:

结果并不相等,并且相差还不少。
其结果也就说明了浮点数在大数的标识精度不好,只能近似标识,同时也说明了为什么一般不使用浮点数相等来进行判断的原因。
这也是为什么有时候明明我们采用直接编码用准确的浮点数,到了浮点数变量里面却损失了精度,因为4个字节的float标识不了,只能近似处理。
3、非要判断相等
由于有些应用非要使用浮点数进行相等的处理,我们不应该直接使用浮点数进行等于号的判断,而是要在一定的误差和精度范围内进行满足。
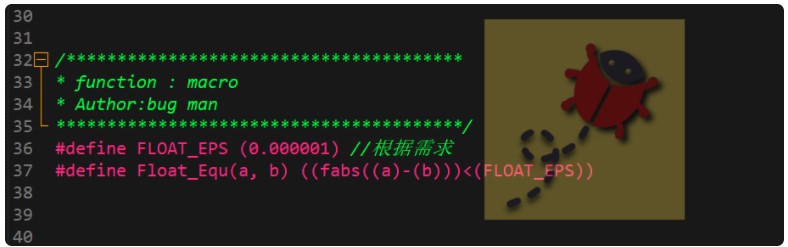
如上图所示代码是比较常用的处理办法,在往期的文章中,bug菌没有详细的讲解这个误差宏的定义,前面了解到当数据比较大的时候相邻的差值会比较大,这样就存在两个浮点数的差值大于所设置的误差范围而无法判断相等。
所以这样的处理办法来判断浮点数近似相等会存在一些局限性。
那有没有相对更好一点的办法呢?
当然是有的,不然接下来没得写了。
还是要从浮点数的存储和标识出发来处理该问题,既然浮点数天然就存在一定的误差,而有时候计算又无法获得唯一的数值,如下图所示,浮点数计算出来的实轴上的值都会因为浮点数无法存储标识而近似到其相邻的可以标识的数值上。
从浮点的存储模型来看,指数部分代表着浮点数的范围,尾数部分代表着浮点数的精度,那么尾数的最后一位其实就表示了浮点数的当前数值附近的精度。
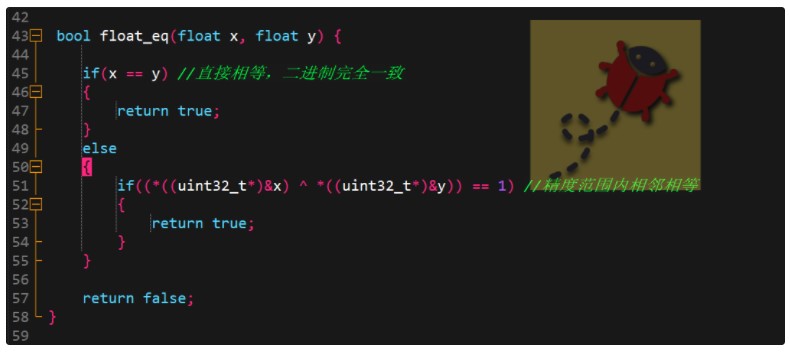
于是对浮点的近似相等进行了算法上的修改,如下代码所示:
解释一下 :
如果直接相等,说明浮点数各数据位都相等;而如果不相等可能相邻,于是强制转化为整形,比较尾数最后一位是否不同。
这里使用一个小技巧,采用异或的处理办法,如果其他位都相同,而最后一位不同,结果就等于1,认为两个浮点数近似相等。
本文到此结束,我相信大家应该对浮点数有了一个更加深入的了解,面对一些问题心中也会有一些答案,比如浮点数为什么不能作为switch的参数,也是同样的原因。
但总的来说还是建议大家不要判断浮点数相等,非要用也要特别小心。
审核编辑:刘清
-
Switch
+关注
关注
1文章
541浏览量
61352 -
数据存储
+关注
关注
5文章
1014浏览量
52590 -
浮点数
+关注
关注
0文章
62浏览量
16354
发布评论请先 登录
浮点数的表示方法

单片机浮点数运算的源码设计

什么是浮点数
定点数和浮点数的概念 浮点数二进制序列与指数表达式之间的转化





 谈一谈浮点数的精度问题
谈一谈浮点数的精度问题













评论