基础算法:差分数组详解

读完本文，可以去力扣解决如下题目：

370. 区间加法（中等）

1109. 航班预订统计（中等）

1094. 拼车（中等）

PS：这是一年前发布的论那些小而美的算法技巧：差分数组/前缀和，我优化并添加了很多内容，重新发一遍。

前文说前缀和主要适用的场景是原始数组不会被修改的情况下，频繁查询某个区间的累加和。

这里简单介绍一下前缀和，核心代码就是下面这段：

classPrefixSum{
//前缀和数组
privateint[]prefix;

/*输入一个数组，构造前缀和*/
publicPrefixSum(int[]nums){
prefix=newint[nums.length+1];
//计算nums的累加和
for(inti=1;i< prefix.length; i++) {
            prefix[i] = prefix[i - 1]+nums[i-1];
}
}

/*查询闭区间[i,j]的累加和*/
publicintquery(inti,intj){
returnprefix[j+1]-prefix[i];
}
}

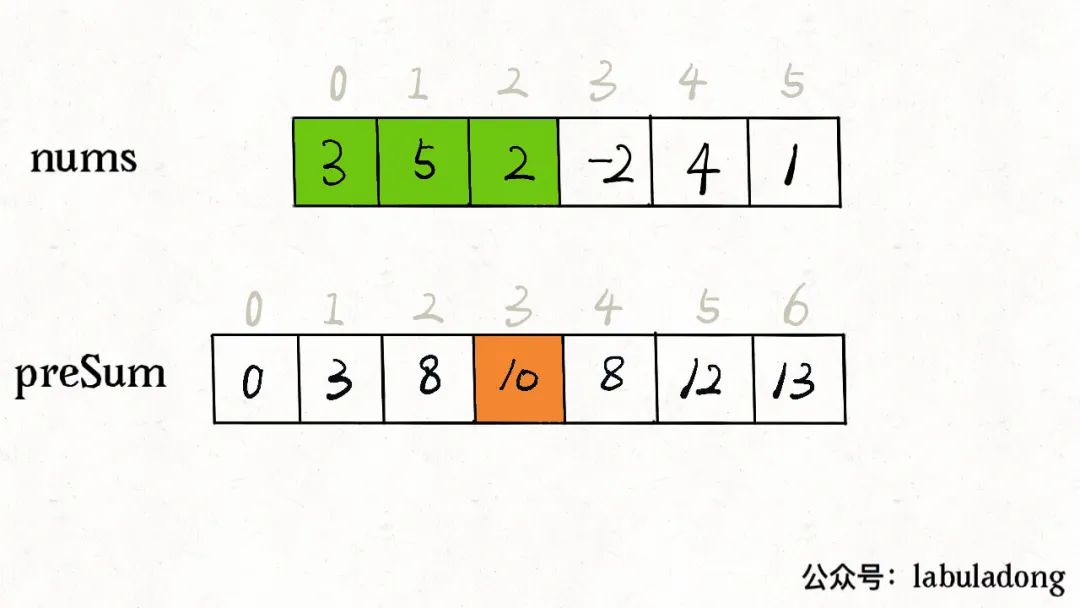
prefix[i]就代表着nums[0..i-1]所有元素的累加和，如果我们想求区间nums[i..j]的累加和，只要计算prefix[j+1] - prefix[i]即可，而不需要遍历整个区间求和。

本文讲一个和前缀和思想非常类似的算法技巧「差分数组」，差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。

比如说，我给你输入一个数组nums，然后又要求给区间nums[2..6]全部加 1，再给nums[3..9]全部减 3，再给nums[0..4]全部加 2，再给…

一通操作猛如虎，然后问你，最后nums数组的值是什么？

常规的思路很容易，你让我给区间nums[i..j]加上val，那我就一个 for 循环给它们都加上呗，还能咋样？这种思路的时间复杂度是 O(N)，由于这个场景下对nums的修改非常频繁，所以效率会很低下。

这里就需要差分数组的技巧，类似前缀和技巧构造的prefix数组，我们先对nums数组构造一个diff差分数组，diff[i]就是nums[i]和nums[i-1]之差：

int[]diff=newint[nums.length];
//构造差分数组
diff[0]=nums[0];
for(inti=1;i< nums.length; i++) {
    diff[i] = nums[i] - nums[i - 1];
}

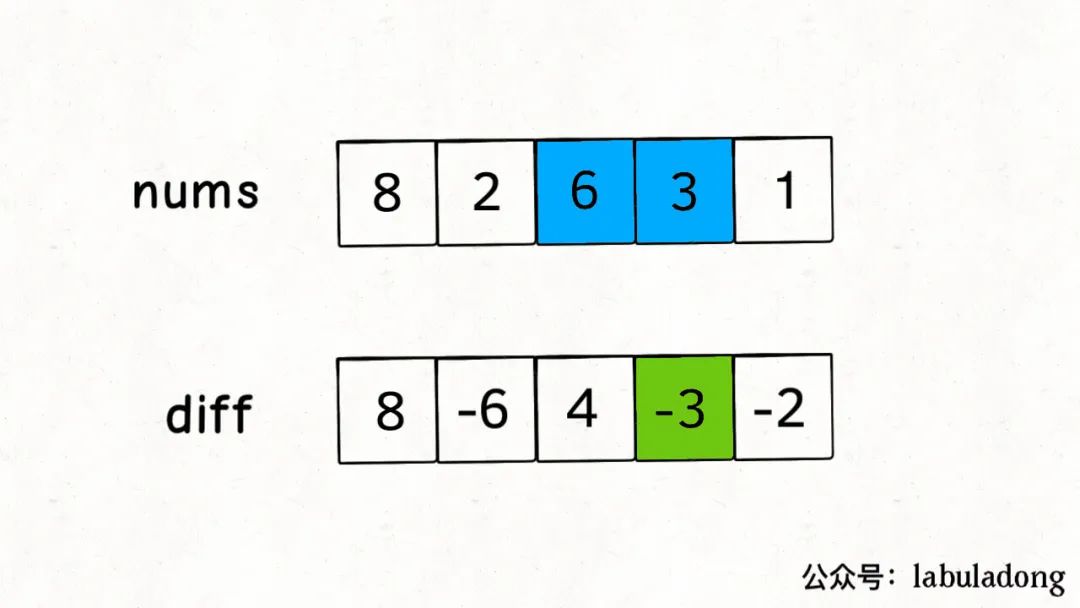
通过这个diff差分数组是可以反推出原始数组nums的，代码逻辑如下：

int[]res=newint[diff.length];
//根据差分数组构造结果数组
res[0]=diff[0];
for(inti=1;i< diff.length; i++) {
    res[i] = res[i - 1]+diff[i];
}

这样构造差分数组diff，就可以快速进行区间增减的操作，如果你想对区间nums[i..j]的元素全部加 3，那么只需要让diff[i] += 3，然后再让diff[j+1] -= 3即可：

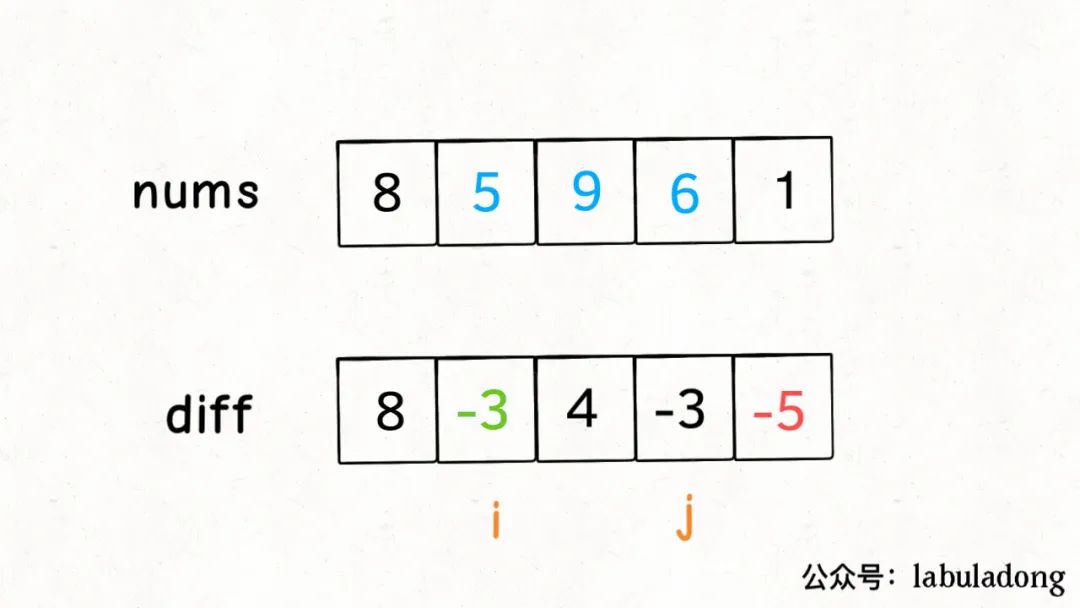
原理很简单，回想diff数组反推nums数组的过程，diff[i] += 3意味着给nums[i..]所有的元素都加了 3，然后diff[j+1] -= 3又意味着对于nums[j+1..]所有元素再减 3，那综合起来，是不是就是对nums[i..j]中的所有元素都加 3 了？

只要花费 O(1) 的时间修改diff数组，就相当于给nums的整个区间做了修改。多次修改diff，然后通过diff数组反推，即可得到nums修改后的结果。

现在我们把差分数组抽象成一个类，包含increment方法和result方法：

//差分数组工具类
classDifference{
//差分数组
privateint[]diff;

/*输入一个初始数组，区间操作将在这个数组上进行*/
publicDifference(int[]nums){
assertnums.length>0;
diff=newint[nums.length];
//根据初始数组构造差分数组
diff[0]=nums[0];
for(inti=1;i< nums.length; i++) {
            diff[i] = nums[i] - nums[i - 1];
}
}

/*给闭区间[i,j]增加val（可以是负数）*/
publicvoidincrement(inti,intj,intval){
diff[i]+=val;
if(j+1< diff.length) {
            diff[j + 1]-=val;
}
}

/*返回结果数组*/
publicint[]result(){
int[]res=newint[diff.length];
//根据差分数组构造结果数组
res[0]=diff[0];
for(inti=1;i< diff.length; i++) {
            res[i] = res[i - 1]+diff[i];
}
returnres;
}
}

这里注意一下increment方法中的 if 语句：

publicvoidincrement(inti,intj,intval){
diff[i]+=val;
if(j+1< diff.length) {
        diff[j + 1]-=val;
}
}

当j+1 >= diff.length时，说明是对nums[i]及以后的整个数组都进行修改，那么就不需要再给diff数组减val了。

算法实践

首先，力扣第 370 题「区间加法」 就直接考察了差分数组技巧：

那么我们直接复用刚才实现的Difference类就能把这道题解决掉：

int[]getModifiedArray(intlength,int[][]updates){
//nums初始化为全0
int[]nums=newint[length];
//构造差分解法
Differencedf=newDifference(nums);

for(int[]update:updates){
inti=update[0];
intj=update[1];
intval=update[2];
df.increment(i,j,val);
}

returndf.result();
}

当然，实际的算法题可能需要我们对题目进行联想和抽象，不会这么直接地让你看出来要用差分数组技巧，这里看一下力扣第 1109 题「航班预订统计」：

函数签名如下：

int[]corpFlightBookings(int[][]bookings,intn)

这个题目就在那绕弯弯，其实它就是个差分数组的题，我给你翻译一下：

给你输入一个长度为n的数组nums，其中所有元素都是 0。再给你输入一个bookings，里面是若干三元组(i,j,k)，每个三元组的含义就是要求你给nums数组的闭区间[i-1,j-1]中所有元素都加上k。请你返回最后的nums数组是多少？

PS：因为题目说的n是从 1 开始计数的，而数组索引从 0 开始，所以对于输入的三元组(i,j,k)，数组区间应该对应[i-1,j-1]。

这么一看，不就是一道标准的差分数组题嘛？我们可以直接复用刚才写的类：

int[]corpFlightBookings(int[][]bookings,intn){
//nums初始化为全0
int[]nums=newint[n];
//构造差分解法
Differencedf=newDifference(nums);

for(int[]booking:bookings){
//注意转成数组索引要减一哦
inti=booking[0]-1;
intj=booking[1]-1;
intval=booking[2];
//对区间nums[i..j]增加val
df.increment(i,j,val);
}
//返回最终的结果数组
returndf.result();
}

这道题就解决了。

还有一道很类似的题目是力扣第 1094 题「拼车」，我简单描述下题目：

你是一个开公交车的司机，公交车的最大载客量为capacity，沿途要经过若干车站，给你一份乘客行程表int[][] trips，其中trips[i] = [num, start, end]代表着有num个旅客要从站点start上车，到站点end下车，请你计算是否能够一次把所有旅客运送完毕（不能超过最大载客量capacity）。

函数签名如下：

booleancarPooling(int[][]trips,intcapacity);

比如输入：

trips=[[2,1,5],[3,3,7]],capacity=4

这就不能一次运完，因为trips[1]最多只能上 2 人，否则车就会超载。

相信你已经能够联想到差分数组技巧了：trips[i]代表着一组区间操作，旅客的上车和下车就相当于数组的区间加减；只要结果数组中的元素都小于capacity，就说明可以不超载运输所有旅客。

但问题是，差分数组的长度（车站的个数）应该是多少呢？题目没有直接给，但给出了数据取值范围：

0<= trips[i][1] < trips[i][2] <= 1000

车站个数最多为 1000，那么我们的差分数组长度可以直接设置为 1001：

booleancarPooling(int[][]trips,intcapacity){
//最多有1000个车站
int[]nums=newint[1001];
//构造差分解法
Differencedf=newDifference(nums);

for(int[]trip:trips){
//乘客数量
intval=trip[0];
//第trip[1]站乘客上车
inti=trip[1];
//第trip[2]站乘客已经下车，
//即乘客在车上的区间是[trip[1],trip[2]-1]
intj=trip[2]-1;
//进行区间操作
df.increment(i,j,val);
}

int[]res=df.result();

//客车自始至终都不应该超载
for(inti=0;i< res.length; i++) {
        if(capacity< res[i]) {
            returnfalse;
}
}
returntrue;
}

至此，这道题也解决了。

最后，差分数组和前缀和数组都是比较常见且巧妙的算法技巧，分别适用不同的常见，而且是会者不难，难者不会。所以，关于差分数组的使用，你学会了吗？

原文标题：小而美的算法技巧：差分数组

文章出处：【微信公众号：算法与数据结构】欢迎添加关注！文章转载请注明出处。
审核编辑：汤梓红