一道比较有难度的完美矩形题

今天讲一道非常有意思，而且比较有难度的题目。

我们知道一个矩形有四个顶点，但是只要两个顶点的坐标就可以确定一个矩形了（比如左下角和右上角两个顶点坐标）。

来看看力扣第 391 题「完美矩形」，题目会给我们输入一个数组rectangles，里面装着若干四元组（x1，y1，x2，y2），每个四元组就是记录一个矩形的左下角和右上角顶点坐标。

也就是说，输入的rectangles数组实际上就是很多小矩形，题目要求我们输出一个布尔值，判断这些小矩形能否构成一个「完美矩形」。函数签名如下：

defisRectangleCover(rectangles:List[List[int]])->bool

所谓「完美矩形」，就是说rectangles中的小矩形拼成图形必须是一个大矩形，且大矩形中不能有重叠和空缺。

比如说题目给我们举了几个例子：

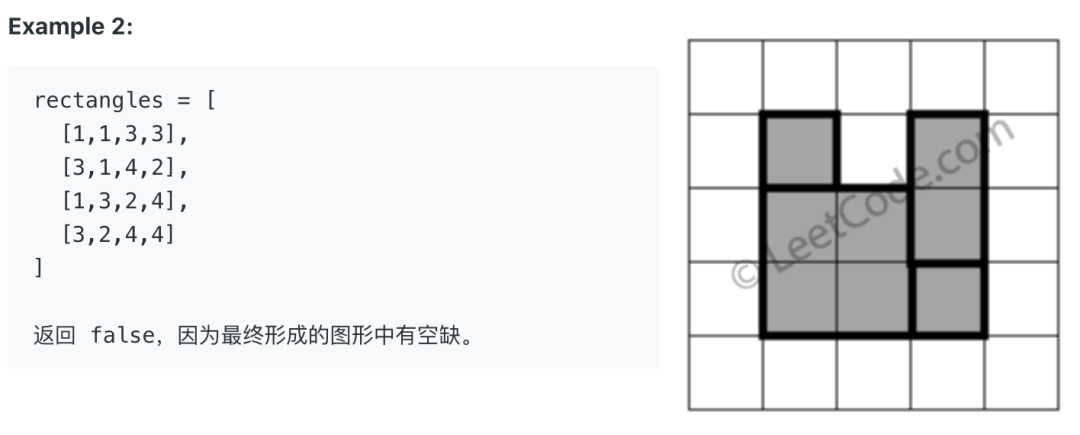
这个题目难度是 Hard，如果没有做过类似的题目，还真做不出来。

常规的思路，起码要把最终形成的图形表示出来吧，而且你要有方法去判断两个矩形是否有重叠，是否有空隙，虽然可以做到，不过感觉异常复杂。

其实，想判断最终形成的图形是否是完美矩形，需要从「面积」和「顶点」两个角度来处理。

先说说什么叫从「面积」的角度。

rectangles数组中每个元素都是一个四元组（x1， y1， x2， y2），表示一个小矩形的左下角顶点坐标和右上角顶点坐标。

那么假设这些小矩形最终形成了一个「完美矩形」，你会不会求这个完美矩形的左下角顶点坐标（X1， Y1）和右上角顶点的坐标（X2， Y2）？

这个很简单吧，左下角顶点（X1， Y1）就是rectangles中所有小矩形中最靠左下角的那个小矩形的左下角顶点；右上角顶点（X2， Y2）就是所有小矩形中最靠右上角的那个小矩形的右上角顶点。

注意我们用小写字母表示小矩形的坐标，大写字母表示最终形成的完美矩形的坐标，可以这样写代码：

#左下角顶点，初始化为正无穷，以便记录最小值
X1,Y1=float('inf'),float('inf')
#右上角顶点，初始化为负无穷，以便记录最大值
X2,Y2=-float('inf'),-float('inf')

forx1,y1,x2,y2inrectangles:
#取小矩形左下角顶点的最小值
X1,Y1=min(X1,x1),min(Y1,y1)
#取小矩形右上角顶点的最大值
X2,Y2=max(X2,x2),max(Y2,y2)

这样就能求出完美矩形的左下角顶点坐标（X1， Y1）和右上角顶点的坐标（X2， Y2）了。

计算出的X1，Y1，X2，Y2坐标是完美矩形的「理论坐标」，如果所有小矩形的面积之和不等于这个完美矩形的理论面积，那么说明最终形成的图形肯定存在空缺或者重叠，肯定不是完美矩形。

代码可以进一步：

defisRectangleCover(rectangles:List[List[int]])->bool:
X1,Y1=float('inf'),float('inf')
X2,Y2=-float('inf'),-float('inf')
#记录所有小矩形的面积之和
actual_area=0
forx1,y1,x2,y2inrectangles:
#计算完美矩形的理论坐标
X1,Y1=min(X1,x1),min(Y1,y1)
X2,Y2=max(X2,x2),max(Y2,y2)
#累加所有小矩形的面积
actual_area+=(x2-x1)*(y2-y1)

#计算完美矩形的理论面积
expected_area=(X2-X1)*(Y2-Y1)
#面积应该相同
ifactual_area!=expected_area:
returnFalse

returnTrue

这样，「面积」这个维度就完成了，思路其实不难，无非就是假设最终形成的图形是个完美矩形，然后比较面积是否相等，如果不相等的话说明最终形成的图形一定存在空缺或者重叠部分，不是完美矩形。

但是反过来说，如果面积相同，是否可以证明最终形成的图形是完美矩形，一定不存在空缺或者重叠？

肯定是不行的，举个很简单的例子，你假想一个完美矩形，然后我在它中间挖掉一个小矩形，把这个小矩形向下平移一个单位。这样小矩形的面积之和没变，但是原来的完美矩形中就空缺了一部分，也重叠了一部分，已经不是完美矩形了。

综上，即便面积相同，并不能完全保证不存在空缺或者重叠，所以我们需要从「顶点」的维度来辅助判断。

记得小学的时候有一道智力题，给你一个矩形，切一刀，剩下的图形有几个顶点？答案是，如果沿着对角线切，就剩 3 个顶点；如果横着或者竖着切，剩 4 个顶点；如果只切掉一个小角，那么会出现 5 个顶点。

回到这道题，我们接下来的分析也有那么一点智力题的味道。

显然，完美矩形一定只有四个顶点。矩形嘛，按理说应该有四个顶点，如果存在空缺或者重叠的话，肯定不是四个顶点，比如说题目的这两个例子就有不止 4 个顶点：

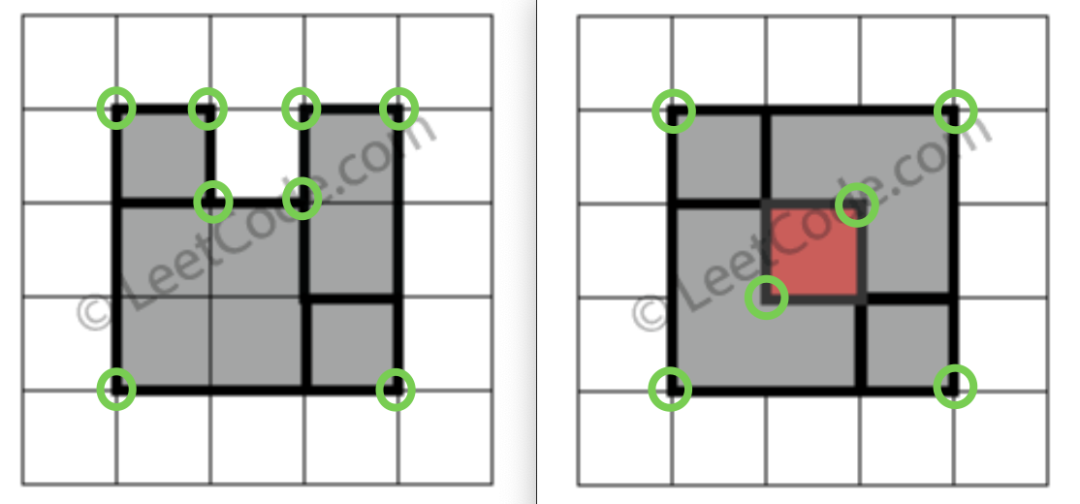
PS：我也不知道应该用「顶点」还是「角」来形容，好像都不太准确，本文统一用「顶点」来形容，大家理解就好~

只要我们想办法计算rectangles中的小矩形最终形成的图形有几个顶点，就能判断最终的图形是不是一个完美矩形了。

那么顶点是如何形成的呢？我们倒是一眼就可以看出来顶点在哪里，问题是如何让计算机，让算法知道某一个点是不是顶点呢？这也是本题的难点所在。

看下图的四种情况：

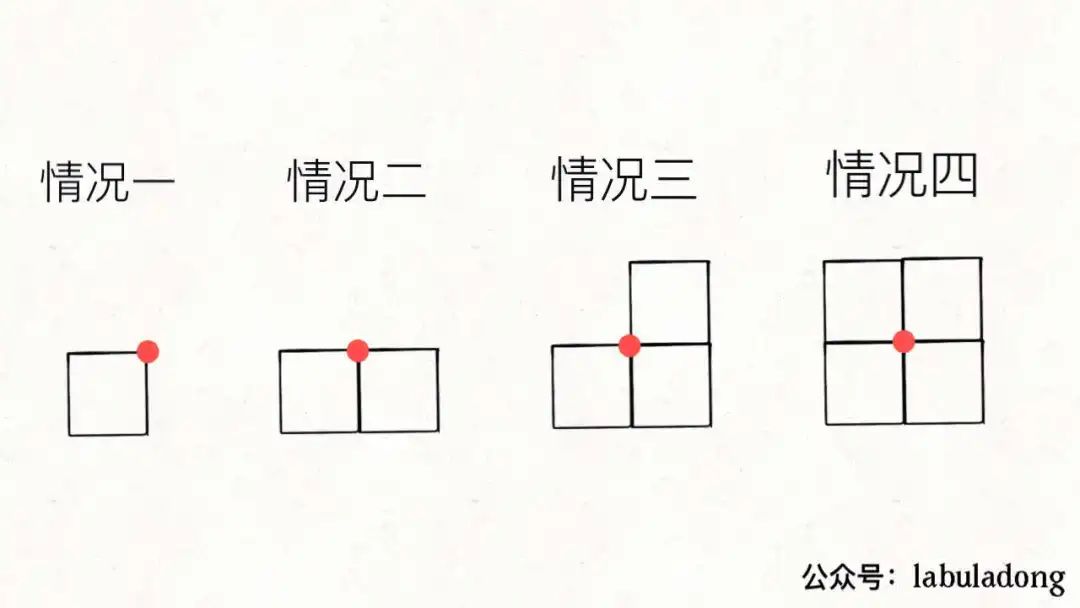
图中画红点的地方，什么时候是顶点，什么时候不是顶点？显然，情况一和情况三的时候是顶点，而情况二和情况四的时候不是顶点。

也就是说，当某一个点同时是 2 个或者 4 个小矩形的顶点时，该点最终不是顶点；当某一个点同时是 1 个或者 3 个小矩形的顶点时，该点最终是一个顶点。

注意，2 和 4 都是偶数，1 和 3 都是奇数，我们想计算最终形成的图形中有几个顶点，也就是要筛选出那些出现了奇数次的顶点，可以这样写代码：

defisRectangleCover(rectangles:List[List[int]])->bool:
X1,Y1=float('inf'),float('inf')
X2,Y2=-float('inf'),-float('inf')

actual_area=0
#哈希集合，记录最终图形的顶点
points=set()
forx1,y1,x2,y2inrectangles:
X1,Y1=min(X1,x1),min(Y1,y1)
X2,Y2=max(X2,x2),max(Y2,y2)

actual_area+=(x2-x1)*(y2-y1)
#先算出小矩形每个点的坐标
p1,p2=(x1,y1),(x1,y2)
p3,p4=(x2,y1),(x2,y2)
#对于每个点，如果存在集合中，删除它；
#如果不存在集合中，添加它；
#在集合中剩下的点都是出现奇数次的点
forpin[p1,p2,p3,p4]:
ifpinpoints:points.remove(p)
else:points.add(p)

expected_area=(X2-X1)*(Y2-Y1)
ifactual_area!=expected_area:
returnFalse

returnTrue

这段代码中，我们用一个points集合记录rectangles中小矩形组成的最终图形的顶点坐标，关键逻辑在于如何向points中添加坐标：

如果某一个顶点p存在于集合points中，则将它删除；如果不存在于集合points中，则将它插入。

这个简单的逻辑，让points集合最终只会留下那些出现了 1 次或者 3 次的顶点，那些出现了 2 次或者 4 次的顶点都被消掉了。

那么首先想到，points集合中最后应该只有 4 个顶点对吧，如果len（points） ！= 4说明最终构成的图形肯定不是完美矩形。

但是如果len（points） == 4是否能说明最终构成的图形肯定是完美矩形呢？也不行，因为题目并没有说rectangles中的小矩形不存在重复，比如下面这种情况：

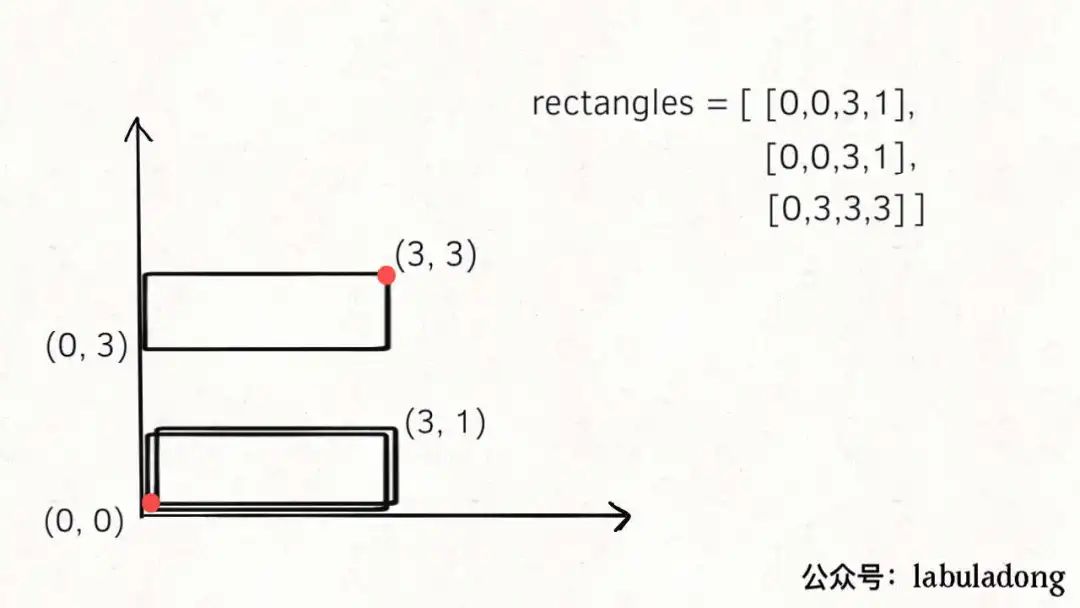
下面两个矩形重复了，按照我们的算法逻辑，它们的顶点都被消掉了，最终是剩下了四个顶点；再看面积，完美矩形的理论坐标是图中红色的点，计算出的理论面积和实际面积也相同。但是显然这种情况不是题目要求完美矩形。

所以不仅要保证len（points） == 4，而且要保证points中最终剩下的点坐标就是完美矩形的四个理论坐标，直接看代码吧：

defisRectangleCover(rectangles:List[List[int]])->bool:
X1,Y1=float('inf'),float('inf')
X2,Y2=-float('inf'),-float('inf')

points=set()
actual_area=0
forx1,y1,x2,y2inrectangles:
#计算完美矩形的理论顶点坐标
X1,Y1=min(X1,x1),min(Y1,y1)
X2,Y2=max(X2,x2),max(Y2,y2)
#累加小矩形的面积
actual_area+=(x2-x1)*(y2-y1)
#记录最终形成的图形中的顶点
p1,p2=(x1,y1),(x1,y2)
p3,p4=(x2,y1),(x2,y2)
forpin[p1,p2,p3,p4]:
ifpinpoints:points.remove(p)
else:points.add(p)
#判断面积是否相同
expected_area=(X2-X1)*(Y2-Y1)
ifactual_area!=expected_area:
returnFalse
#判断最终留下的顶点个数是否为4
iflen(points)!=4:returnFalse
#判断留下的4个顶点是否是完美矩形的顶点
if(X1,Y1)notinpoints:returnFalse
if(X1,Y2)notinpoints:returnFalse
if(X2,Y1)notinpoints:returnFalse
if(X2,Y2)notinpoints:returnFalse
#面积和顶点都对应，说明矩形符合题意
returnTrue

这就是最终的解法代码，从「面积」和「顶点」两个维度来判断：

1、判断面积，通过完美矩形的理论坐标计算出一个理论面积，然后和rectangles中小矩形的实际面积和做对比。

2、判断顶点，points集合中应该只剩下 4 个顶点且剩下的顶点必须都是完美矩形的理论顶点。

说实话，如果没做过，这种特性真不是一时半会能想到的，但是看过一遍没问题了，你学会了吗？

责任编辑：xj

原文标题：这道「完美矩形」给我整不会了…

文章出处：【微信公众号：算法与数据结构】欢迎添加关注！文章转载请注明出处。