二叉树操作的相关知识和代码详解

树是数据结构中的重中之重，尤其以各类二叉树为学习的难点。在面试环节中，二叉树也是必考的模块。本文主要讲二叉树操作的相关知识，梳理面试常考的内容。请大家跟随小编一起来复习吧。

本篇针对面试中常见的二叉树操作作个总结：

前序遍历，中序遍历，后序遍历；

层次遍历；

求树的结点数；

求树的叶子数；

求树的深度；

求二叉树第k层的结点个数；

判断两棵二叉树是否结构相同；

求二叉树的镜像；

求两个结点的最低公共祖先结点；

求任意两结点距离；

找出二叉树中某个结点的所有祖先结点；

不使用递归和栈遍历二叉树；

二叉树前序中序推后序；

判断二叉树是不是完全二叉树；

判断是否是二叉查找树的后序遍历结果；

给定一个二叉查找树中的结点，找出在中序遍历下它的后继和前驱；

二分查找树转化为排序的循环双链表；

有序链表转化为平衡的二分查找树；

判断是否是二叉查找树。

1 前序遍历，中序遍历，后序遍历；

1.1 前序遍历

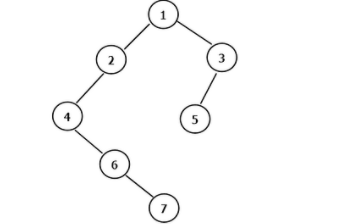
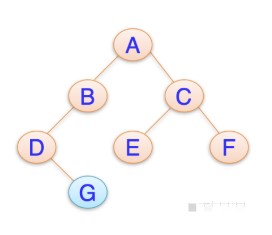
#FormatImgID_0#对于当前结点，先输出该结点，然后输出它的左孩子，最后输出它的右孩子。以上图为例，递归的过程如下：

输出 1，接着左孩子；

输出 2，接着左孩子；

输出 4，左孩子为空，再接着右孩子；

输出 6，左孩子为空，再接着右孩子；

输出 7，左右孩子都为空，此时 2 的左子树全部输出，2 的右子树为空，此时 1 的左子树全部输出，接着 1 的右子树；

输出 3，接着左孩子；

输出 5，左右孩子为空，此时 3 的左子树全部输出，3 的右子树为空，至此 1 的右子树全部输出，结束。

而非递归版本只是利用 stack 模拟上述过程而已，递归的过程也就是出入栈的过程。

/*前序遍历递归版*/

voidPreOrderRec(Node*node)

{

if(node==nullptr)

return;

cout<< node->data<< " ";   // 先输出当前结点   

PreOrderRec(node->left);//然后输出左孩子

PreOrderRec(node->right);//最后输出右孩子

}

/*前序遍历非递归版*/

voidPreOrderNonRec(Node*node)

{

if(node==nullptr)

return;

stackS;

cout<< node->data<< " ";

S.push(node);

node=node->left;

while(!S.empty()||node)

{

while(node)

{

cout<< node->data<< " "; // 先输出当前结点  

S.push(node);

node=node->left;//然后输出左孩子

}//while结束意味着左孩子已经全部输出

node=S.top()->right;//最后输出右孩子

S.pop();

}

}

1.2 中序遍历

对于当前结点，先输出它的左孩子，然后输出该结点，最后输出它的右孩子。以（1.1）图为例：

1-->2-->4，4 的左孩子为空，输出 4，接着右孩子；

6 的左孩子为空，输出 6，接着右孩子；

7 的左孩子为空，输出 7，右孩子也为空，此时 2 的左子树全部输出，输出 2，2 的右孩子为空，此时 1 的左子树全部输出，输出 1，接着 1 的右孩子；

3-->5，5 左孩子为空，输出 5，右孩子也为空，此时 3 的左子树全部输出，而 3 的右孩子为空，至此 1 的右子树全部输出，结束。

/*中序遍历递归版*/

voidInOrderRec(Node*node)

{

if(node==nullptr)

return;

InOrderRec(node->left);//先输出左孩子

cout<< node->data<< " ";  // 然后输出当前结点

InOrderRec(node->right);//最后输出右孩子

}

/*前序遍历非递归版*/

voidInOrderNonRec(Node*node)

{

if(node==nullptr)

return;

stackS;

S.push(node);

node=node->left;

while(!S.empty()||node)

{

while(node)

{

S.push(node);

node=node->left;

}//while结束意味着左孩子为空

cout<< S.top()->data<< " "; // 左孩子已经全部输出，接着输出当前结点

node=S.top()->right;//左孩子全部输出，当前结点也输出后，最后输出右孩子

S.pop();

}

}

1.3 后序遍历

对于当前结点，先输出它的左孩子，然后输出它的右孩子，最后输出该结点。依旧以（1.1）图为例：

1->2->4->6->7，7 无左孩子，也无右孩子，输出 7，此时 6 无左孩子，而 6 的右子树也全部输出，输出 6，此时 4 无左子树，而 4 的右子树已全部输出，接着输出 4，此时 2 的左子树全部输出，且 2 无右子树，输出 2，此时 1 的左子树全部输出，接着转向右子树；

3->5，5 无左孩子，也无右孩子，输出 5，此时 3 的左子树全部输出，且 3 无右孩子，输出 3，此时 1 的右子树全部输出，输出 1，结束。

非递归版本中，对于一个结点，如果我们要输出它，只有它既没有左孩子也没有右孩子或者它有孩子但是它的孩子已经被输出（由此设置 pre 变量）。若非上述两种情况，则将该结点的右孩子和左孩子依次入栈，这样就保证了每次取栈顶元素的时候,先依次遍历左子树和右子树。

/*后序遍历递归版*/

voidPostOrderRec(Node*node)

{

if(node==nullptr)

return;

PostOrderRec(node->left);//先输出左孩子

PostOrderRec(node->right);//然后输出右孩子

cout<< node->data<< " ";  // 最后输出当前结点

}

/*后序遍历非递归版*/

voidPostOrderNonRec(Node*node)

{

if(node==nullptr)

return;

Node*pre=nullptr;

stackS;

S.push(node);

while(!S.empty())

{

node=S.top();

if((!node->left&&!node->right)||//第一个输出的必是无左右孩子的叶子结点，只要第一个结点输出，

(pre &&(pre == node->left || pre == node->right)))//以后的 pre 就不会是空。此处的判断语句加入一个 pre，只是用来

{//确保可以正确输出第一个结点。

cout<< node->data<< " ";  // 左右孩子都全部输出，再输出当前结点

pre=node;

S.pop();

}

else

{

if(node->right)

S.push(node->right);//先进右孩子，再进左孩子，取出来的才是左孩子

if(node->left)

S.push(node->left);

}

}

}

2 层次遍历

voidLevelOrder(Node*node)

{

Node*p=node;

queueQ;//队列

Q.push(p);

while(!Q.empty())

{

p=Q.front();

cout<< p->data<< " ";

Q.pop();

if(p->left)

Q.push(p->left);//注意顺序，先进左孩子

if(p->right)

Q.push(p->right);

}

}

3 求树的结点数

intCountNodes(Node*node)

{

if(node==nullptr)

return0;

returnCountNodes(node->left)+CountNodes(node->right)+1;

}

4 求树的叶子数

intCountLeaves(Node*node)

{

if(node==nullptr)

return0;

if(!node->left&&!node->right)

return1;

returnCountLeaves(node->left)+CountLeaves(node->right);

}

5 求树的深度

intGetDepth(Node*node)

{

if(node==nullptr)

return0;

intleft_depth=GetDepth(node->left)+1;

intright_depth=GetDepth(node->right)+1;

returnleft_depth>right_depth?left_depth:right_depth;

}

6 求二叉树第k层的结点个数

intGetKLevel(Node*node,intk)

{

if(node==nullptr)

return0;

if(k==1)

return1;

returnGetKLevel(node->left,k-1)+GetKLevel(node->right,k-1);

}

7 判断两棵二叉树是否结构相同

不考虑数据内容。结构相同意味着对应的左子树和对应的右子树都结构相同。

boolStructureCmp(Node*node1,Node*node2)

{

if(node1==nullptr&&node2==nullptr)

returntrue;

elseif(node1==nullptr||node2==nullptr)

returnfalse;

returnStructureCmp(node1->left,node2->left)&&Str1uctureCmp(node1->right,node2->right);

}

8 求二叉树的镜像

对于每个结点，我们交换它的左右孩子即可。

voidMirror(Node*node)

{

if(node==nullptr)

return;

Node*temp=node->left;

node->left=node->right;

node->right=temp;

Mirror(node->left);

Mirror(node->right);

}

9 求两个结点的最低公共祖先结点

最低公共祖先，即 LCA（Lowest Common Ancestor），见下图：#FormatImgID_1#结点 3 和结点 4 的最近公共祖先是结点 2，即 LCA(3,4)=2。在此，需要注意到当两个结点在同一棵子树上的情况，如结点 3 和结点 2 的最近公共祖先为 2，即 LCA(3,2)=2。同理 LCA(5,6)=4，LCA(6,10)=1。

Node*FindLCA(Node*node,Node*target1,Node*target2)

{

if(node==nullptr)

returnnullptr;

if(node==target1||node==target2)

returnnode;

Node*left=FindLCA(node->left,target1,target2);

Node*right=FindLCA(node->right,target1,target2);

if(left&&right)//分别在左右子树

returnnode;

returnleft?left:right;//都在左子树或右子树

}

10 求任意两结点距离

#FormatImgID_2#首先找到两个结点的 LCA，然后分别计算 LCA 与它们的距离，最后相加即可。

intFindLevel(Node*node,Node*target)

{

if(node==nullptr)

return-1;

if(node==target)

return0;

intlevel=FindLevel(node->left,target);//先在左子树找

if(level==-1)

level=FindLevel(node->right,target);//如果左子树没找到，在右子树找

if(level!=-1)//找到了，回溯

returnlevel+1;

return-1;//如果左右子树都没找到

}

intDistanceNodes(Node*node,Node*target1,Node*target2)

{

Node*lca=FindLCA(node,target1,target2);//找到最低公共祖先结点

intlevel1=FindLevel(lca,target1);

intlevel2=FindLevel(lca,target2);

returnlevel1+level2;

}

11 找出二叉树中某个结点的所有祖先结点

#FormatImgID_3#如果给定结点 5，则其所有祖先结点为 4,2,1。

boolFindAllAncestors(Node*node,Node*target)

{

if(node==nullptr)

returnfalse;

if(node==target)

returntrue;

if(FindAllAncestors(node->left,target)||FindAllAncestors(node->right,target))//找到了

{

cout<< node->data<< " ";

returntrue;//回溯

}

returnfalse;//如果左右子树都没找到

}

12 不使用递归和栈遍历二叉树

1968 年，高德纳（Donald Knuth）提出一个问题：是否存在一个算法，它不使用栈也不破坏二叉树结构，但是可以完成对二叉树的遍历？随后 1979 年，James H. Morris 提出了二叉树线索化，解决了这个问题。（根据这个概念我们又提出了一个新的数据结构，即线索二叉树，因线索二叉树不是本文要介绍的内容，所以有兴趣的朋友请移步线索二叉树）

前序，中序，后序遍历，不管是递归版本还是非递归版本，都用到了一个数据结构--栈，为何要用栈？那是因为其它的方式没法记录当前结点的 parent,而如果在每个结点的结构里面加个 parent 分量显然是不现实的，而线索化正好解决了这个问题，其含义就是利用结点的右孩子空指针，指向该结点在中序序列中的后继。下面具体来看看如何使用线索化来完成对二叉树的遍历。#FormatImgID_4#先看前序遍历，步骤如下：

如果当前结点的左孩子为空，则输出当前结点并将其右孩子作为当前结点；

如果当前结点的左孩子不为空，在当前结点的左子树中找到当前结点在中序遍历下的前驱结点；

2.1如果前驱结点的右孩子为空，将它的右孩子设置为当前结点，输出当前结点并把当前结点更新为当前结点的左孩子；

2.2如果前驱结点的右孩子为当前结点，将它的右孩子重新设为空，当前结点更新为当前结点的右孩子；

重复以上步骤 1 和 2，直到当前结点为空。

/*前序遍历*/

voidPreOrderMorris(Node*root)

{

Node*cur=root;

Node*pre=nullptr;

while(cur)

{

if(cur->left==nullptr)//步骤1

{

cout<< cur->data<< " ";

cur=cur->right;

}

else

{

pre=cur->left;

while(pre->right&&pre->right!=cur)//步骤2，找到cur的前驱结点

pre=pre->right;

if(pre->right==nullptr)//步骤2.1，cur未被访问，将cur结点作为其前驱结点的右孩子

{

cout<< cur->data<< " ";

pre->right=cur;

cur=cur->left;

}

else//步骤2.2，cur已被访问，恢复树的原有结构，更改right指针

{

pre->right=nullptr;

cur=cur->right;

}

}

}

}

再来看中序遍历，和前序遍历相比只改动一句代码，步骤如下：

如果当前结点的左孩子为空，则输出当前结点并将其右孩子作为当前结点；

如果当前结点的左孩子不为空，在当前结点的左子树中找到当前结点在中序遍历下的前驱结点；

2.1. 如果前驱结点的右孩子为空，将它的右孩子设置为当前结点，当前结点更新为当前结点的左孩子；

2.2. 如果前驱结点的右孩子为当前结点，将它的右孩子重新设为空，输出当前结点，当前结点更新为当前结点的右孩子；

重复以上步骤 1 和 2，直到当前结点为空。

/*中序遍历*/

voidInOrderMorris(Node*root)

{

Node*cur=root;

Node*pre=nullptr;

while(cur)

{

if(cur->left==nullptr)//（1）

{

cout<< cur->data<< " ";

cur=cur->right;

}

else

{

pre=cur->left;

while(pre->right&&pre->right!=cur)//（2），找到cur的前驱结点

pre=pre->right;

if(pre->right==nullptr)//（2.1），cur未被访问，将cur结点作为其前驱结点的右孩子

{

pre->right=cur;

cur=cur->left;

}

else//（2.2），cur已被访问，恢复树的原有结构，更改right指针

{

cout<< cur->data<< " ";

pre->right=nullptr;

cur=cur->right;

}

}

}

}

最后看下后序遍历，后序遍历有点复杂，需要建立一个虚假根结点 dummy，令其左孩子是 root。并且还需要一个子过程，就是倒序输出某两个结点之间路径上的各个结点。#FormatImgID_5#步骤如下：

如果当前结点的左孩子为空，则将其右孩子作为当前结点；

如果当前结点的左孩子不为空，在当前结点的左子树中找到当前结点在中序遍历下的前驱结点；

2.1. 如果前驱结点的右孩子为空，将它的右孩子设置为当前结点，当前结点更新为当前结点的左孩子；

2.2. 如果前驱结点的右孩子为当前结点，将它的右孩子重新设为空，倒序输出从当前结点的左孩子到该前驱结点这条路径上的所有结点，当前结点更新为当前结点的右孩子；

重复以上步骤 1 和 2，直到当前结点为空。

structNode

{

intdata;

Node*left;

Node*right;

Node(intdata_,Node*left_,Node*right_)

{

data=data_;

left=left_;

right=right_;

}

};

voidReversePrint(Node*from,Node*to)

{

if(from==to)

{

cout<< from->data<< " ";

return;

}

ReversePrint(from->right,to);

cout<< from->data<< " ";

}

voidPostOrderMorris(Node*root)

{

Node*dummy=newNode(-1,root,nullptr);//一个虚假根结点

Node*cur=dummy;

Node*pre=nullptr;

while(cur)

{

if(cur->left==nullptr)//步骤1

cur=cur->right;

else

{

pre=cur->left;

while(pre->right&&pre->right!=cur)//步骤2，找到cur的前驱结点

pre=pre->right;

if(pre->right==nullptr)//步骤2.1，cur未被访问，将cur结点作为其前驱结点的右孩子

{

pre->right=cur;

cur=cur->left;

}

else//步骤2.2，cur已被访问，恢复树的原有结构，更改right指针

{

pre->right=nullptr;

ReversePrint(cur->left,pre);

cur=cur->right;

}

}

}

}

dummy 用的非常巧妙，建议读者配合上面的图模拟下算法流程。

13 二叉树前序中序推后序

方式	序列
前序	[1 2 4 7 3 5 8 9 6]
中序	[4 7 2 1 8 5 9 3 6]
后序	[7 4 2 8 9 5 6 3 1]

以上面图表为例，步骤如下：

根据前序可知根结点为1；

根据中序可知 4 7 2 为根结点 1 的左子树和 8 5 9 3 6 为根结点 1 的右子树；

递归实现，把 4 7 2 当做新的一棵树和 8 5 9 3 6 也当做新的一棵树；

在递归的过程中输出后序。

/*前序遍历和中序遍历结果以长度为n的数组存储，pos1为前序数组下标，pos2为后序下标*/

intpre_order_arry[n];

intin_order_arry[n];

voidPrintPostOrder(intpos1,intpos2,intn)

{

if(n==1)

{

cout<< pre_order_arry[pos1];

return;

}

if(n==0)

return;

inti=0;

for(;pre_order_arry[pos1]!=in_order_arry[pos2+i];i++)

;

PrintPostOrder(pos1+1,pos2,i);

PrintPostOrder(pos1+i+1,pos2+i+1,n-i-1);

cout<< pre_order_arry[pos1];

}

当然我们也可以根据前序和中序构造出二叉树，进而求出后序。

/*该函数返回二叉树的根结点*/

Node*Create(intpos1,intpos2,intn)

{

Node*p=nullptr;

for(inti=0;i< n; i++)

{

if(pre_order_arry[pos1]==in_order_arry[pos2+i])

{

p=newNode(pre_order_arry[pos1]);

p->left=Create(pos1+1,pos2,i);

p->right=Create(pos1+i+1,pos2+i+1,n-i-1);

returnp;

}

}

returnp;

}

14 判断二叉树是不是完全二叉树

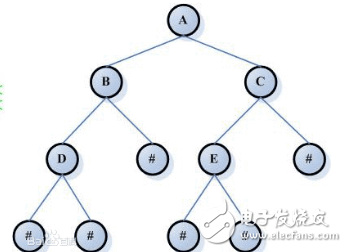
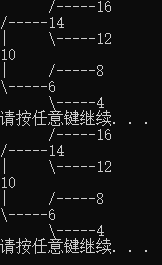
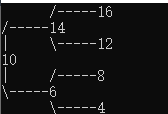
若设二叉树的深度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树（Complete Binary Tree）。如下图：#FormatImgID_6#

首先若一个结点只有右孩子，肯定不是完全二叉树；其次若只有左孩子或没有孩子，那么接下来的所有结点肯定都没有孩子，否则就不是完全二叉树，因此设置 flag 标记变量。

boolIsCBT(Node*node)

{

boolflag=false;

queueQ;

Q.push(node);

while(!Q.empty())

{

Node*p=Q.front();

Q.pop();

if(flag)

{

if(p->left||p->right)

returnfalse;

}

else

{

if(p->left&&p->right)

{

Q.push(p->left);

Q.push(p->right);

}

elseif(p->right)//只有右结点

returnfalse;

elseif(p->left)//只有左结点

{

Q.push(p->left);

flag=true;

}

else//没有结点

flag=true;

}

}

returntrue;

}

15 判断是否是二叉查找树的后序遍历结果

在后续遍历得到的序列中，最后一个元素为树的根结点。从头开始扫描这个序列，比根结点小的元素都应该位于序列的左半部分；从第一个大于跟结点开始到跟结点前面的一个元素为止，所有元素都应该大于跟结点，因为这部分元素对应的是树的右子树。根据这样的划分，把序列划分为左右两部分，我们递归地确认序列的左、右两部分是不是都是二元查找树。

intarray[n];//长度为n的序列，注意begin和end遵循的是左闭右闭原则

boolIsSequenceOfBST(intbegin,intend)

{

if(end-begin<= 0)

returntrue;

introot_data=array[end];//数组尾元素为根结点

inti=begin;

for(;array[i]< root_data; i++) // 取得左子树

;

intj=i;

for(;j< end; j++)

if(array[j]< root_data)  // 此时右子树应该都大于根结点；若存在小于，直接 return false

returnfalse;

returnIsSequenceOfBST(begin,i-1)&&IsSequenceOfBST(i,end-1);//左右子树是否都满足

}

16 给定一个二叉查找树中的结点（存在一个指向父亲结点的指针），找出在中序遍历下它的后继和前驱

一棵二叉查找树的中序遍历序列，正好是升序序列。假如根结点的父结点为 nullptr，则：

如果当前结点有右孩子，则后继结点为这个右孩子的最左孩子；

如果当前结点没有右孩子；

2.1. 当前结点为根结点，返回 nullptr；

2.2. 当前结点只是个普通结点，也就是存在父结点；

2.2.1. 当前结点是父亲结点的左孩子，则父亲结点就是后继结点；

2.2.2. 当前结点是父亲结点的右孩子，沿着父亲结点往上走，直到 n-1 代祖先是 n 代祖先的左孩子，则后继为 n 代祖先或遍历到根结点也没找到符合的，则当前结点就是中序遍历的最后一个结点，返回 nullptr。

/*求后继结点*/

Node*Increment(Node*node)

{

if(node->right)//步骤1

{

node=node->right;

while(node->left)

node=node->left;

returnnode;

}

else//步骤2

{

if(node->parent==nullptr)//步骤2.1

returnnullptr;

Node*p=node->parent;//步骤2.2

if(p->left==node)//步骤2.2.1

returnp;

else//步骤2.2.2

{

while(p->right==node)

{

node=p;

p=p->parent;

if(p==nullptr)

returnnullptr;

}

returnp;

}

}

}

仔细观察上述代码，总觉得有点啰嗦。比如，过多的 return，步骤 2 的层次太多。综合考虑所有情况，改进代码如下：

Node*Increment(Node*node)

{

if(node->right)

{

node=node->right;

while(node->left)

node=node->left;

}

else

{

Node*p=node->parent;

while(p&&p->right==node)

{

node=p;

p=p->parent;

}

node=p;

}

returnnode;

}

上述的代码是基于结点有 parent 指针的，若题意要求没有 parent 呢？网上也有人给出了答案，个人觉得没有什么价值，有兴趣的朋友可以到这里查看。

而求前驱结点的话，只需把上述代码的 left 与 right 互调即可，很简单。

17 二分查找树转化为排序的循环双链表

二分查找树的中序遍历即为升序排列，问题就在于如何在遍历的时候更改指针的指向。一种简单的方法时，遍历二分查找树，将遍历的结果放在一个数组中，之后再把该数组转化为双链表。如果题目要求只能使用 O(1)O(1) 内存，则只能在遍历的同时构建双链表，即进行指针的替换。

我们需要用递归的方法来解决，假定每个递归调用都会返回构建好的双链表，可把问题分解为左右两个子树。由于左右子树都已经是有序的，当前结点作为中间的一个结点，把左右子树得到的链表连接起来即可。

/*合并两个a,b两个循环双向链表*/

Node*Append(Node*a,Node*b)

{

if(a==nullptr)returnb;

if(b==nullptr)returna;

//分别得到两个链表的最后一个元素

Node*a_last=a->left;

Node*b_last=b->left;

//将两个链表头尾相连

a_last->right=b;

b->left=a_last;

a->left=b_last;

b_last->right=a;

returna;

}

/*递归的解决二叉树转换为双链表*/

Node*TreeToList(Node*node)

{

if(node==nullptr)returnnullptr;

//递归解决子树

Node*left_list=TreeToList(node->left);

Node*right_list=TreeToList(node->right);

//把根结点转换为一个结点的双链表，方便后面的链表合并

node->left=node;

node->right=node;

//合并之后即为升序排列

left_list=Append(left_list,node);

left_list=Append(left_list,right_list);

returnleft_list;

}

18 有序链表转化为平衡的二分查找树（Binary Search Tree）

我们可以采用自顶向下的方法。先找到中间结点作为根结点，然后递归左右两部分。所以我们需要先找到中间结点，对于单链表来说，必须要遍历一边，可以使用快慢指针加快查找速度。

structTreeNode

{

intdata;

TreeNode*left;

TreeNode*right;

TreeNode(intdata_){data=data_;left=right=nullptr;}

};

structListNode

{

intdata;

ListNode*next;

ListNode(intdata_){data=data_;next=nullptr;}

};

TreeNode*SortedListToBST(ListNode*list_node)

{

if(!list_node)returnnullptr;

if(!list_node->next)return(newTreeNode(list_node->data));

//用快慢指针找到中间结点

ListNode*pre_slow=nullptr;//记录慢指针的前一个结点

ListNode*slow=list_node;//慢指针

ListNode*fast=list_node;//快指针

while(fast&&fast->next)

{

pre_slow=slow;

slow=slow->next;

fast=fast->next->next;

}

TreeNode*mid=newTreeNode(slow->data);

//分别递归左右两部分

if(pre_slow)

{

pre_slow->next=nullptr;

mid->left=SortedListToBST(list_node);

}

mid->right=SortedListToBST(slow->next);

returnmid;

}

由 f(n)=2f(\frac n2)+\frac n2f(n)=2f(2n)+2n 得，所以上述算法的时间复杂度为 O(nlogn)O(nlogn)。

不妨换个思路，采用自底向上的方法：

TreeNode*SortedListToBSTRec(ListNode*&list,intstart,intend)

{

if(start>end)returnnullptr;

intmid=start+(end-start)/2;

TreeNode*left_child=SortedListToBSTRec(list,start,mid-1);//注意此处传入的是引用

TreeNode*parent=newTreeNode(list->data);

parent->left=left_child;

list=list->next;

parent->right=SortedListToBSTRec(list,mid+1,end);

returnparent;

}

TreeNode*SortedListToBST(ListNode*node)

{

intn=0;

ListNode*p=node;

while(p)

{

n++;

p=p->next;

}

returnSortedListToBSTRec(node,0,n-1);

}

如此，时间复杂度降为 O(n)O(n)。

19 判断是否是二叉查找树

我们假定二叉树没有重复元素，即对于每个结点，其左右孩子都是严格的小于和大于。

下面给出两个方法：

方法 1：

boolIsBST(Node*node,intmin,intmax)

{

if(node==nullptr)

returntrue;

if(node->data<= min || node->data>=max)

returnfalse;

returnIsBST(node->left,min,node->data)&&IsBST(node->right,node->data,max);

}

IsBST(node,INT_MIN,INT_MAX);

方法 2：

利用二叉查找树中序遍历时元素递增来判断。

boolIsBST(Node*node)

{

staticintpre=INT_MIN;

if(node==nullptr)

returntrue;

if(!IsBST(node->left))

returnfalse;

if(node->data< pre)

returnfalse;

pre=node->data;

returnIsBST(node->right);

}