详解一道高频算法题：括号生成

题目描述

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[ "((()))", "(()())", "(())()", "()(())", "()()()" ] 题目解析

方法一：回溯算法（深度优先遍历）

如果完成一件事情有很多种方法，并且每一种方法分成若干步骤，那多半就可以使用“回溯”算法完成。

“回溯”算法的基本思想是“尝试搜索”，一条路如果走不通（不能得到想要的结果），就回到上一个“路口”，尝试走另一条路。

因此，“回溯”算法的时间复杂度一般不低。如果能提前分析出，走这一条路并不能得到想要的结果，可以跳过这个分支，这一步操作叫“剪枝”。

做“回溯”算法问题的基本套路是：

1、使用题目中给出的示例，画树形结构图，以便分析出递归结构；

一般来说，树形图不用画完，就能够分析出递归结构和解题思路。

2、分析一个结点可以产生枝叶的条件、递归到哪里终止、是否可以剪枝、符合题意的结果在什么地方出现（可能在叶子结点，也可能在中间的结点）；

3、完成以上两步以后，就要编写代码实现上述分析的过程，使用代码在画出的树形结构上搜索符合题意的结果。

在树形结构上搜索结果集，使用的方法是执行一次“深度优先遍历”。在遍历的过程中，可能需要使用“状态变量”。

（“广度优先遍历”当然也是可以的，请参考方法二。）

我们以 n = 2 为例，画树形结构图。

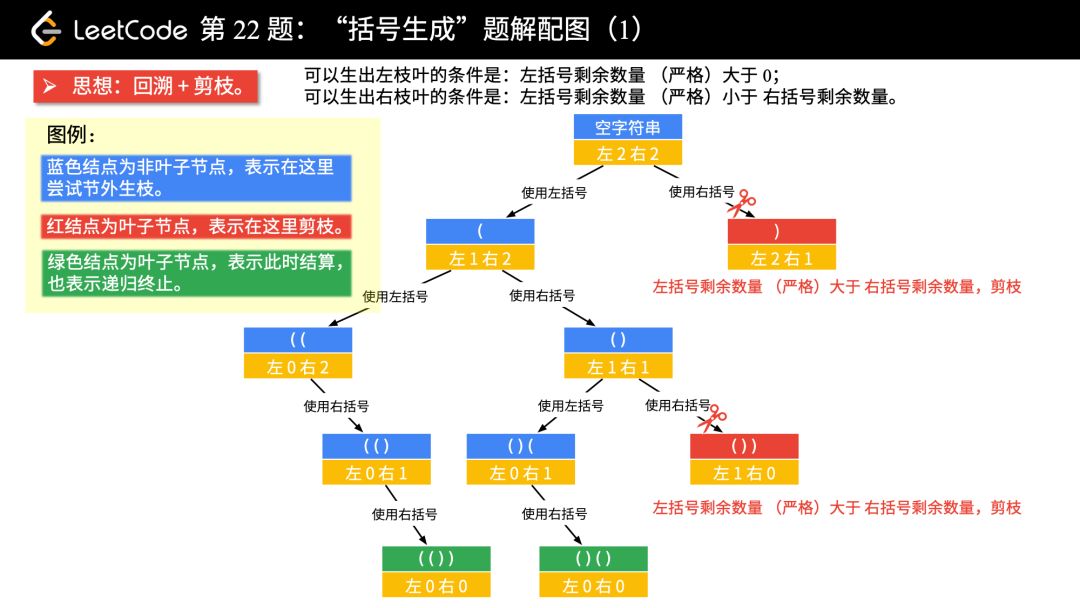
题解配图(1)

画图以后，可以分析出的结论：

左右都有可以使用的括号数量，即严格大于 0 的时候，才产生分支；

左边不受右边的限制，它只受自己的约束；

右边除了自己的限制以外，还收到左边的限制，即：右边剩余可以使用的括号数量一定得在严格大于左边剩余的数量的时候，才可以“节外生枝”；

在左边和右边剩余的括号数都等于 0 的时候结算。

参考代码如下：

publicclassSolution{ publicListgenerateParenthesis(intn){ Listres=newArrayList<>(); //特判 if(n==0){ returnres; } //执行深度优先遍历，搜索可能的结果 dfs("",n,n,res); returnres; } /** *@paramcurStr当前递归得到的结果 *@paramleft左括号还有几个没有用掉 *@paramright右边的括号还有几个没有用掉 *@paramres结果集 */ privatevoiddfs(StringcurStr,intleft,intright,Listres){ //因为是递归函数，所以先写递归终止条件 if(left==0&&right==0){ res.add(curStr); return; } //因为每一次尝试，都使用新的字符串变量，所以没有显式的回溯过程 //在递归终止的时候，直接把它添加到结果集即可，与「力扣」第46题、第39题区分 //如果左边还有剩余，继续递归下去 if(left>0){ //拼接上一个左括号，并且剩余的左括号个数减1 dfs(curStr+"(",left-1,right,res); } //什么时候可以用右边？例如，(((((()，此时 left < right，         // 不能用等号，因为只有先拼了左括号，才能拼上右括号         if (right >0&&left< right) {             // 拼接上一个右括号，并且剩余的右括号个数减 1             dfs(curStr + ")", left, right - 1, res);         }     } }

如果我们不用减法，使用加法，即 left 表示“左括号还有几个没有用掉”，right 表示“右括号还有几个没有用掉”，可以画出另一棵递归树。

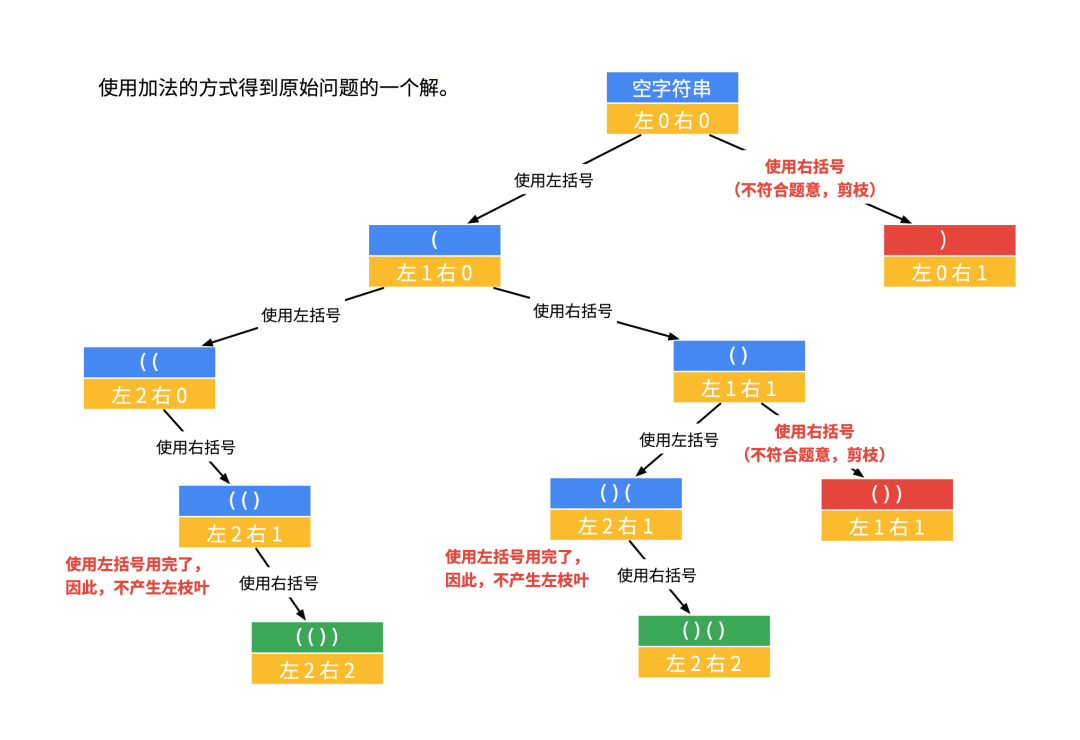
题解配图(2)

参考代码如下：

publicclassSolution{ //方法 2：用加法 publicListgenerateParenthesis(intn){ Listres=newArrayList<>(); //特判 if(n==0){ returnres; } //这里的dfs是隐式回溯 dfs("",0,0,n,res); returnres; } /** *@paramcurStr当前递归得到的结果 *@paramleft左括号用了几个 *@paramright右括号用了几个 *@paramn左括号、右括号一共用几个 *@paramres结果集 */ privatevoiddfs(StringcurStr,intleft,intright,intn,Listres){ //因为是递归函数，所以先写递归终止条件 if(left==n&&right==n){ res.add(curStr); return; } //如果左括号还没凑够，继续凑 if(left< n) {             // 拼接上一个左括号，并且剩余的左括号个数减 1             dfs(curStr + "(", left + 1, right, n, res);         }         // 什么时候可以用右边？例如，(((((()，此时 left > right， //不能用等号，因为只有先拼了左括号，才能拼上右括号 if(right< n && left >right){ //拼接上一个右括号，并且剩余的右括号个数减1 dfs(curStr+")",left,right+1,n,res); } } }

方法二：广度优先遍历

还是上面的题解配图（1），使用广度优先遍历，结果集都在最后一层，即叶子结点处得到所有的结果集，编写代码如下。

publicclassSolution{ classNode{ /** *当前得到的字符串 */ privateStringres; /** *剩余左括号数量 */ privateintleft; /** *剩余右括号数量 */ privateintright; publicNode(Stringres,intleft,intright){ this.res=res; this.left=left; this.right=right; } @Override publicStringtoString(){ return"Node{"+ "res='"+res+'''+ ",left="+left+ ",right="+right+ '}'; } } publicListgenerateParenthesis(intn){ Listres=newArrayList<>(); if(n==0){ returnres; } Queuequeue=newLinkedList<>(); queue.offer(newNode("",n,n)); //总共需要拼凑的字符总数是2*n n=2*n; while(n>0){ intsize=queue.size(); for(inti=0;i< size; i++) {                 Node curNode = queue.poll();                 if (curNode.left >0){ queue.offer(newNode(curNode.res+"(",curNode.left-1,curNode.right)); } if(curNode.right>0&&curNode.left< curNode.right) {                     queue.offer(new Node(curNode.res + ")", curNode.left, curNode.right - 1));                 }             }             n--;         }         // 最后一层就是题目要求的结果集         while (!queue.isEmpty()) {             res.add(queue.poll().res);         }         return res;     } } 

方法三：动态规划

第 1 步：定义状态 dp[i]

使用 i 对括号能够生成的组合。

注意：每一个状态都是列表的形式。

第 2 步：状态转移方程：

i 对括号的一个组合，在 i - 1 对括号的基础上得到；

i 对括号的一个组合，一定以左括号 "(" 开始（不一定以 ")" 结尾），为此，我们可以枚举右括号 ")" 的位置，得到所有的组合；

枚举的方式就是枚举左括号 "(" 和右括号 ")" 中间可能的合法的括号对数，而剩下的合法的括号对数在与第一个左括号 "(" 配对的右括号 ")" 的后面，这就用到了以前的状态。

状态转移方程是：

dp[i] = "(" + dp[可能的括号对数] + ")" + dp[剩下的括号对数]

“可能的括号对数” 与 “剩下的括号对数” 之和得为 i，故“可能的括号对数” j 可以从 0 开始，最多不能超过 i， 即 i - 1；

“剩下的括号对数” + j = i - 1，故 “剩下的括号对数” = i - j - 1。

整理得：

dp[i] = "(" + dp[j] + ")" + dp[i- j - 1] , j = 0, 1, ..., i - 1

第 3 步：思考初始状态和输出：

初始状态：因为我们需要 0 对括号这种状态，因此状态数组 dp 从 0 开始，0 个括号当然就是 [""]。
输出：dp[n] 。
这个方法暂且就叫它动态规划，这么用也是很神奇的，它有下面两个特点：

1、自底向上：从小规模问题开始，逐渐得到大规模问题的解集；

2、无后效性：后面的结果的得到，不会影响到前面的结果。

publicclassSolution{ //把结果集保存在动态规划的数组里 publicListgenerateParenthesis(intn){ if(n==0){ returnnewArrayList<>(); } //这里dp数组我们把它变成列表的样子，方便调用而已 List>dp=newArrayList<>(n); Listdp0=newArrayList<>(); dp0.add(""); dp.add(dp0); for(inti=1;i<= n; i++) {             Listcur=newArrayList<>(); for(intj=0;j< i; j++) {                 Liststr1=dp.get(j); Liststr2=dp.get(i-1-j); for(Strings1:str1){ for(Strings2:str2){ //枚举右括号的位置 cur.add("("+s1+")"+s2); } } } dp.add(cur); } returndp.get(n); } }