Leetcode 最新上线了手机版 APP,今天蹲坑的时候随手翻了一道题,一道和栈有关的题目,大概知道了解题思路,就点开了题解准备看看别人是如何写代码的,没想到最后一种解法让我感觉自己的智商受到了碾压。
题目描述
给定一个只包含'('和')'的字符串,找出最长的包含有效括号的子串的长度。
示例 1:
输入:"(()" 输出:2 解释:最长有效括号子串为"()"
示例 2:
输入:")()())" 输出:4 解释:最长有效括号子串为"()()"
题目解析
解法一:栈
一开始看到这个题目,有点熟悉的感觉:相当于是 LeetCode 第 20 题有效的括号的升级版。
想到这立马尝试借助栈这个数据结构去解决。
括号相关的问题首先可以尝试使用栈这个数据结构去解决,至于原因,想一想应该不难理解,如果进来一个右括号,也就是 ')',它会和之前最后一次遍历到的左括号匹配,栈的先进后出的特性保证了这一要求。
对于这道题目,因为我们要求的是子串的长度,因此我们可以考虑在栈中保存index,这样子我们不仅可以通过index找到对应的括号,还可以借此来求长度,我们的思路可以分为下面几步:
1、从左到右遍历输入的字符串
2、如果遇到的是'(',意味着这并不能和前面遍历过的部分组成合法答案,此时我们只需要把当前index入栈即可
3、如果遇到的是')',这时我们就要看栈顶保存的元素了,这里就会有几种情况:
栈顶保存的是'(',表示当前元素和栈顶元素可以配对,这个时候我们需要把栈顶元素弹出栈,记录答案则记录当前index和弹出配对元素后的新栈顶index之间的距离,这个地方是重点,如果不理解,你可以思考下面两个例子:
"((()()" "((())"
栈顶保存的是')',如果是这种情况,表示前面没有可配对的 '(',我们此时还是需要把当前index入栈,原因是
我们确定距离需要知道边界,如果不理解,还是有两个例子供你参考:
"))(())" "())()()"
栈是空的,当然在第一种情况中,你弹出栈顶元素后也会使得栈变空,为了避免这种情况,我们可以在最开始的时候推一个-1入栈,这样可以节省我们的判断次数,并且当栈中的没有元素的时候,我们也可以用这个-1来计算当前子串的长度,你可以参考下面这两个例子:
"()" "()(())"
代码实现
publicintlongestValidParentheses(Strings){ if(s==null||s.length()==0){ return0; } intn=s.length(); char[]sArr=s.toCharArray(); Stack
解法二:动态规划
如果用栈来解决的话,这道题思路差不多就是这样。考虑到前不久一直聊动态规划,于是试了一下用把它归纳到序列型动态规划来求解。
动态规划之空间优化与总结回顾
我们可以定义dp[i] 表示的是 str[0…i] 的答案,思路其实和前面很类似:
1、从左到右遍历输入的字符串
2、如果遇到的是 '(',意味着这并不能和前面遍历过的部分组成合法答案,因为 dp 状态数组中记录的是答案,这个时候说明 dp[i] = 0,也就是不用做任何记录
3、如果遇到的是 ')',这时我们还是需要往前看:
如果 str[i - 1] 是 '(',那么 dp[i] = dp[i - 2] + 2
如果 str[i - 1] 是 ')',这表示 str[i - 1] 已经配对了,因此我们还要继续往前看,从当前位置往左,看第一个没有被配对的 '(',怎么找这个位置呢,这里我们就可以利用 dp[i - 1] 这个信息,dp[i - 1] 表示的是之前匹配的长度,那么 :
i - dp[i - 1] - 1表示的就是从当前位置往左,第一个没有被配对的位置
如果位置 i 和 位置 i - dp[i - 1] - 1 配对后,我们可以看看当前的序列是否可以和之前匹配的序列链接起来,也就是加上 dp[i - dp[i - 1] - 2]
代码实现
publicintlongestValidParentheses(Strings){ if(s==null||s.length()==0){ return0; } intn=s.length(); char[]sArr=s.toCharArray(); int[]dp=newint[n]; intresult=0; for(inti=1;i< n; ++i) { if (sArr[i] == ')') { // 如果前一个位置是 '(',直接配对 if (sArr[i - 1] == '(') { dp[i] = (i >=2?dp[i-2]:0)+2; } //前一个位置是')' //我们从当前位置往左看,如果第一个没有被匹配的位置是'(' //表明当前位置是可以被匹配的 elseif(i-dp[i-1]-1>=0&&sArr[i-dp[i-1]-1]=='('){ //这里其实是dp[i]=i-(i-dp[i-1]-1)+1=dp[i-1]+2 //但是我们还需要考虑之前的答案,也就是dp[i-dp[i-1]-2] //首先判断i-dp[i-1]-2是否越界 //如果没有越界就将其加上 dp[i]=dp[i-1]+2; if(i-dp[i-1]>=2){ dp[i]+=dp[i-dp[i-1]-2]; } } result=Math.max(result,dp[i]); } } returnresult; }
两种方法时空复杂度都是 O(n),解法也有相似之处,只是说切题点不一样。
正当我美滋滋时,突然看到另外一种解法,让我感觉自己的智商受到了碾压:不需要额外的空间,空间复杂度是 O(1)!
解法三:借助变量
使用了两个变量 Left 和 Right,分别用来记录到当前位置时左括号和右括号的出现次数。
当遇到左括号时,Left 自增 1,右括号时 Right 自增1。
对于最长有效的括号的子串,一定是左括号等于右括号的情况,此时就可以更新结果 res 了,一旦右括号数量超过左括号数量了,说明当前位置不能组成合法括号子串,Left 和 Right 重置为 0。
但是对于这种情况 "(()" 时,在遍历结束时左右子括号数都不相等,此时没法更新结果 res,但其实正确答案是 2,怎么处理这种情况呢?
答案是再反向遍历一遍,采取类似的机制,稍有不同的是此时若 Left 大于 Right 了,则重置 0,这样就可以涵盖所有情况。
代码实现
//代码来源:https://leetcode-cn.com/problems/longest-valid-parentheses/solution/zui-chang-you-xiao-gua-hao-by-leetcode/ publicclassSolution{ publicintlongestValidParentheses(Strings){ intleft=0,right=0,maxlength=0; for(inti=0;i< s.length(); i++) { if (s.charAt(i) == '(') { left++; } else { right++; } if (left == right) { maxlength = Math.max(maxlength, 2 * right); } else if (right >=left){ left=right=0; } } left=right=0; for(inti=s.length()-1;i>=0;i--){ if(s.charAt(i)=='('){ left++; }else{ right++; } if(left==right){ maxlength=Math.max(maxlength,2*left); }elseif(left>=right){ left=right=0; } } returnmaxlength; } }
事实上,我在利用解法一求解完这道题目后还怡然自得,认为这道题目最简单的解法就是借助栈这种数据结构,没想到还有解法三这么巧妙的解法。。。
-
数据结构
+关注
关注
3文章
573浏览量
41374 -
leetcode
+关注
关注
0文章
20浏览量
2517
原文标题:一道 LeetCode 的多种解法,打消了我的自以为是!
文章出处:【微信号:TheAlgorithm,微信公众号:算法与数据结构】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
车载屏幕基础可靠性功能测试:守护智能座舱的“第一道防线”

点焊机如何成为动力电池安全的第一道防线?
不间断电源(UPS):电力保障的“最后一道防线”

铅酸蓄电池在线监测:为关键基础设施筑牢“最后一道防线”
顶坚国产防爆手持终端如何成为石化企业安全生产的第一道防线

测试测量仪器对SMA公头的性能要求

聚徽制造业专属工业触摸屏:精准控制每一道工序,提升生产精度
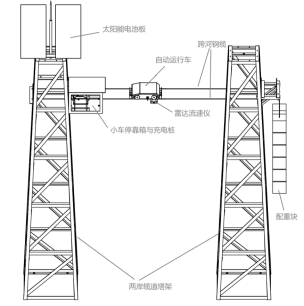
水文监测中的双轨缆道小车和铅鱼缆道小车

成品电池综合测试仪:电池品质的最后一道把关人
AMD携多样化产品组合亮相ISE 2025
DAC8718当转换到第二通道时,第一通道转换出来的信号是否会一直持续不变?
可道云电脑搭建教程,可道云电脑搭建的使用教程





 一道LeetCode的多种解法
一道LeetCode的多种解法











评论