这样一个同步Buck变换器就产生了。可以将电感在不同的位置放置变换为不同的拓扑结构,放在输入端就是Boost变换器,放在下面就是Buck-boost变换器。所以,基本的变换器其实就只有这三种,其他
2022-11-09 10:10:09 2039
2039 
Buck变换器的输出电容是整个Buck电路重要的组成部分,输出电容的作用就是将输出电压稳定在期望的电压值,减少电压的波动。
2022-12-29 09:22:15 3593
3593 基于Buck-Boost的非隔离型双向半桥DCDC变换器结构上比起隔离型的双向DCDC变换器结构简单,没有变压器,功率开关器件数目相对较少,操控方式较容易,通过全控型开关器件的反并联二极管最终
2023-02-25 13:52:17 7390
7390 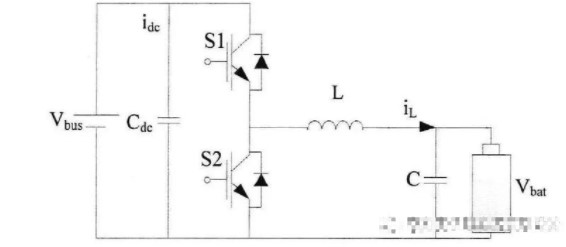
前面介绍了四种基本的非隔离DC-DC变换器结构,它们有一个共同点就是输入输出存在直接的电气连接,然而在实际应用中,由于电压等级变换、安全、系统串并联等原因,需要进行输入和输出的电气隔离
2023-04-11 11:49:39 3323
3323 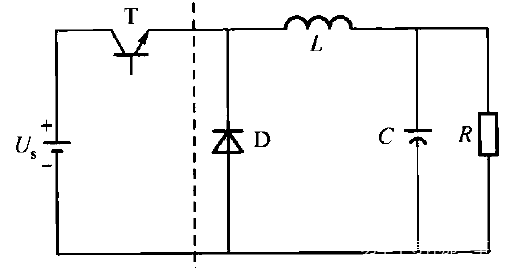
Buck变换器是开关电源基本拓扑结构的一种,在此基础上增加负压输出的功能,甚至比电荷泵电路还要简单。
2023-04-20 14:31:06 844
844 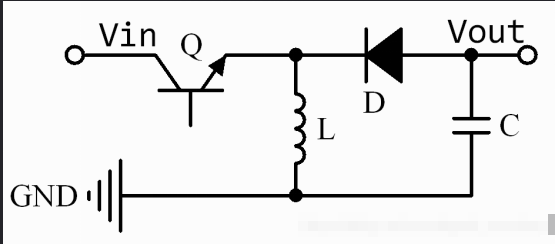
前言:以Buck变换器为例,对小纹波近似、电感伏秒平衡以及电容安秒平衡进行解释说明。
2023-06-23 09:16:00 1169
1169 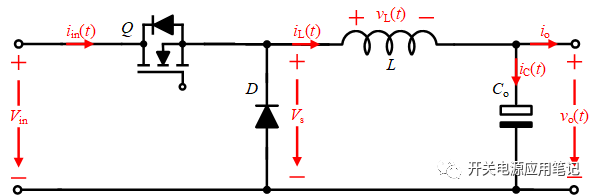
Buck变换器又称降压变换器、串联开关稳压电源、三端开关型降压稳压器。学过电子的应该都知道,如何从一个电压(高)得到自己想要的电压值(低),可能最简单的方式就是通过电阻分压,如下面的方式。
2023-06-26 09:06:24 414
414 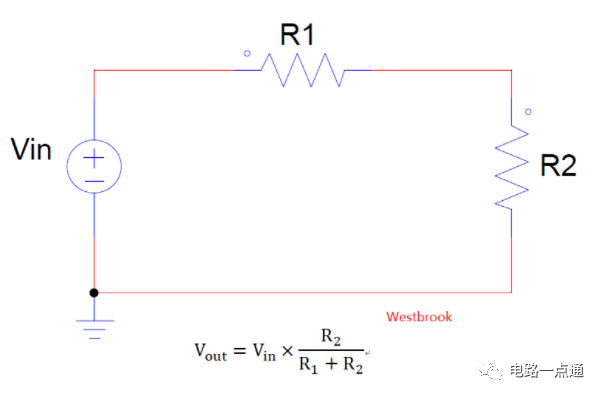
BUCK变换器
2012-08-14 13:05:11
Buck变换器由功率级和反馈控制电路组成,功率级包括功率开关和输出滤波器,它将高输入电压变换到低的输出电压,反馈控制电路通过调制功率开关的占空比调节输出电压。 开关模式的DC-DC变换器的稳态工作
2016-10-10 13:12:34
右SmartyPants创建一个自定义列表如何创建一个注脚注释也是必不可少的KaTeX数学公式新的甘特图功能,丰富你的文章UML 图表FLowchart流程图导出与导入导出导入1.前言在DCDC变换器中BUCK变换器是最基础的一类降压型变换器,它可以将输入电压新的改变我们对Markdown编辑器进
2021-12-30 07:15:00
的BUCK,主要采用PSIM仿真,适用于需要设计此变换器的课设同学。一、设计指标及要求BUCK变换器有关指标为: 输入电压:标称直流48V,范围: 43V~53V 输出电压:直流25V, 4A 输出电压纹波: 100mV 电流纹波: 0.25A 开关频率: 250kHz
2021-11-16 07:22:02
重要标志。如何对一个系统进行建模分析、补偿校正变得越来越重要。 本文选择BUCK型DC/DC变换器作为载体,
2021-06-30 08:14:09
BUCK和BOOST变换器电感的设计0 前言1 确定电流纹波比2 分清变换器的最坏工作状态3 伏秒平衡4 计算实例5 电感选型0 前言对于电源工程师来说,设计中小功率Buck或Boost的基本任务
2021-10-29 06:35:08
1.前言在DCDC变换器中BUCK变换器是最基础的一类降压型变换器,它可以将输入电压降低后输出。在连续模式CCM下,输出和输入之间的比值是D(D为占空比)。这种开关变换器是一种通过电子开关周期分合
2021-10-29 07:26:40
Buck-Boost变换器:既可以升压又可以降压,其简单电路组成如下其中的器件和Buck电路完全一致,只是开关SW,二极管和电感的位置发生了改变Buck-Boost变换器输出的是相对地的负压假设当前
2021-10-29 09:14:37
Buck变换器TC2575欠压锁定电路的典型应用。 TC2575系列稳压器是单片集成电路,非常适合简单方便地设计降压型开关稳压器(降压转换器)。该系列的所有电路均能够驱动1.0A负载,具有出色的线路和负载调节性能。这些器件提供3.3V,5V,12V的固定输出电压和可调输出版本
2019-05-08 09:37:35
一、Buck变换器(降压型)CCM (ContinuousConduction Mode),连续导通模式:在一个开关周期内,电感电流从不会到0。或者说电感从不“复位”,意味着在开关周期内电感磁通从不
2021-11-16 07:00:12
,为了提升效率,可以将续流二极管更换为MOSFET,如下:这样一个同步Buck变换器就产生了。可以将电感在不同的位置放置变换为不同的拓扑结构,放在输入端就是Boost变换器,放在下面就是
2023-03-20 09:24:37
一、Buck变换器另外三种叫法 1.降压变换器:输出电压小于输入电压。 2.串联开关稳压电源:单刀双掷开关(晶体管)串联于输入与输出之间。 3.三端开关型降压稳压电源: 1)输入与输出
2023-03-15 16:20:45
Buck变换器也称降压式变换器,是一种输出电压小于输入电压的单管不隔离直流变换器。图中,Q为开关管,其驱动电压一般为PWM(Pulse、width、modulation脉宽调制)信号,信号周期为Ts
2021-03-18 09:28:25
变换器拓扑是buck级联推挽,后级推挽开环控制,前级buck采用闭环控制,在进行小信号建模的时候,buck电路的输出阻抗可以直接按照它输出的电流电压计算得到的电阻算,还是要等效为后级推挽的输入阻抗呢
2020-11-17 19:36:57
。上面讲到的三种拓扑是电源的最基本拓扑,其他拓扑都是靠它们衍生出来的拓扑,比如反激的前身是buck-boost,正激的前身是buck。搞透了这三个拓扑结构的原理和公式的来龙去脉,其他硬开关的拓扑结构变换器的计算完全可以自己推导出来。
2021-04-20 06:00:00
。上面讲到的三种拓扑是电源的最基本拓扑,其他拓扑都是靠它们衍生出来的拓扑,比如反激的前身是buck-boost,正激的前身是buck。搞透了这三个拓扑结构的原理和公式的来龙去脉,其他硬开关的拓扑结构变换器的计算完全可以自己推导出来。
2021-05-10 09:24:51
状态。3 Boost-Buck光伏接口变换器控制策略3.1 Boost-Buck光伏接口变换器 Boost-Buck光伏接口变换器结构如图3所示。Upv为光伏阵列输出电压;Uo为变换器输出电压;L1
2019-06-03 05:00:03
上一节提到的开关电源的系统框图中,DC-DC变换器是其中一个重要的组成部分DC-DC变换器最基础的主要有三种:Buck变换器,Boost变换器和Buck-Boost变换器Buck变换器:即降压变换器
2021-10-29 06:52:05
前言DC-DC变换器的应用场景为:移动电子设备供电。其中包括,DC/DC开关电源与LDO线性电源。高兴LED电源。功率优化器。如功率跟踪器。与高频变压器结合。分类主要分为隔离性与非隔离型,其中从
2021-11-17 06:54:16
DCDC降压型BUCK变换器应用于汽车电子系统中会出现哪些问题?DCDC降压型BUCK变换器应用于汽车电子系统中的设计技巧有哪些?
2021-07-28 07:36:25
结构和单片集成式两种。典型的变换方法有4种:积分恢复型、电压反馈型、交替积分型和恒流开关型。单片集成的U/F和F/U变换器常采用恒流开关型,通常都是可逆的,既可作为U/F使用,也可作为F/U使用,具有
2011-11-10 11:28:24
ZCS-PWM Buck变换器的工作原理是什么?与功率场效应管(MOSFET)相比,绝缘栅双极晶体管有什么优点?通过Saber仿真软件对新型ZCS PWM Buck变换器进行的仿真分析如何?
2021-04-07 07:02:40
一些差异,但是他们电路的主框架结构是基本一致的,主要可以分为两个部分:一是实现电能转换的主功率部分,另一部分是实现负反馈控制的控制电路,如图1所示。 图1 Buck变换器电路主框图。 对于不同厂商
2009-03-06 12:49:54
Buck变换器的设计与仿真
2015-05-25 09:58:25
开关管;续流的二极管的导通压降高、损耗大、效率低,用功率MOSFET取代续流二极管,就构成同步BUCK变换器,而下端使用二极管续流的结构称为非同步BUCK变换器。图8:同步和非同步BUCK变换器同步
2019-08-15 04:00:00
boost变换器是什么boost变换器称为并联开关变换器。与buck变换器其不同的是,boost型电感在输入端(开关),buck型电感在输出端。boost型变换器的输出电压Vo总是大于输入电压Vi
2018-08-22 14:00:53
谐振网络通常由多个无源电感或电容组成,由于元件个数和连接方式上的差异。常见实用的谐振变换器拓扑结构大致分为两类:一类是负载谐振型,另一类是开关谐振型。负载谐振型变换器是一种较早提出的结构,注重电源
2020-10-13 16:49:00
单级BUCK-BOOST变换器实现APFC的原理及分析本文分析了用BUCK-BOOST电路和反激变换器隔离实现单级功率因数校正的原理和变换过程,给出了电路的Matlab仿真分析的模型。通过对变换器工作在DCM模式下的电路仿真,验证了此方法有良好的效果。[hide][/hide]
2009-12-10 17:09:18
引言降压型变换器在电子设备中有着广泛的应用,是现代电力电子系统的核心部分,它的运行状态直接影响整个电力电子系统的工作性能。采用线性稳压器通过降压必然会出现电源功率转换效率过低的问题,降压变换器
2018-10-18 16:36:29
基于pwm的buck变换器电路的开环实验怎么做?是使用信号发生器给电路送pwm信号吗?还是其他方法?我是个新手,只懂些理论不会实践,还请大佬不吝赐教,感谢!
2020-09-14 19:52:44
基于pwm的buck变换器电路的开环实验怎么做?是使用信号发生器给电路送pwm信号吗?还是其他方法?我是个新手,只懂些理论不会实践,还请大佬不吝赐教,感谢!
2020-09-14 19:42:55
摘 要:开关磁阻电机驱动系统(SRD)是一种新型无级调速系统。文章以开关磁阻电机的功率变换器为主要研究对象,重点分析了经典的半桥型功率变换电路及一种新型的软开关功率变换电路,并对其进行了
2018-09-27 15:32:13
如果去掉Buck变换器电路中的续流二极管会怎样?
2023-04-24 14:22:44
本帖最后由 jf_57534307 于 2022-3-9 20:09 编辑
设计的用单片机控制的buck变换器,输出电压1-15 V可调,输入20-30V,通过adc采集输出电压,用增量式pid算出pwm波的占空比。输出的电压波形不稳定
2022-03-09 08:37:48
求大神帮助单片机控制的Buck变换器设计与仿真
2016-12-25 14:57:44
用于Buck变换器的TC2574欠压锁定电路的典型应用。 TC2574系列稳压器是单片集成电路,非常适合简单方便地设计降压型开关稳压器(降压转换器)。该系列的所有电路均能够驱动0.5A负载,具有出色的线路和负载调节性能。这些器件提供3.3V,5V,12V的固定输出电压和可调输出版本
2019-05-31 07:41:44
电池驱动系统的设计方面,DC-DC变换器的选择至关重要。最合适的DC-DC变换器才能满足电池分布式并网发电系统的需求。 隔离电压型DC-DC变换器 隔离电压型的DC-DC变换器是目前比较常见
2023-03-03 11:32:05
BUCK:降压变换器BOOST:升压变换器BUCK-BOOST:升降压开关电源FLYBACK:就是反激式隔离电源CCM:continuous conduct mode 电感电流联系DCM:discrete conduct mode电感电流断续VMC:voltage mode
2021-10-29 08:15:07
隔离型Cuk变换器电路
2019-04-11 14:00:55
隔离型双向DCDC变换器-拓扑结构与控制方法*附件:隔离型双向DCDC变换器-拓扑结构与控制方法.pdf
2022-08-23 14:12:56
/boost变换的主电路、控制部分中的采样与调理滤波电路、驱动隔离电路等,最终完成双向DC/DC变换器的硬件平台电路设计与焊接。在设计过程中,注意器件高频开关时存在的振荡等问题,并找到对应的解决方法。技术
2020-04-29 14:14:35
BUCK变换器轻载时三种工作模式原理及应用:降压型Buck 变换器在轻载有三种工作模式:突发模式、跳脉冲模式和强迫连续模式。文中详细的阐述了这三种模式的工作原理,同时介绍了
2009-10-27 22:52:13 75
75 逆向变换器电压关系与Buck-Boost电路拓补结构
Buck-Boost电路:升/降压斩波
2009-05-12 20:53:44 1984
1984 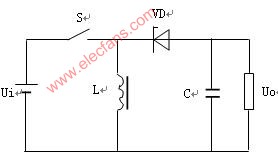
丘克变换器的电压关系及Cuk变换器电路拓补结构
2009-05-12 20:54:10 3332
3332 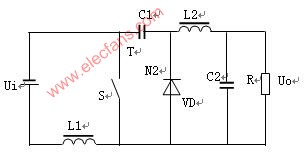
Buck变换器参数辨识的分析
构建了Buck变换器参数辨识的方法。通过检测电感电流和输出电压的波形信号,可辨识出电路的滤波电感、滤波电容及其等
2009-06-30 20:28:59 1303
1303 
Buck变换器的EMC分析
摘要:通过对Buck变换器电路的EMC分析,说明了电磁兼容中滤波、接地、缓冲以及合理的PCB设计等技术在开关电源中的应用。
关键词:开关电
2009-07-04 10:45:01 2362
2362 
Buck变换器的数字模糊PID控制
摘要:由Buck电路的状态空间平均法,可得到其电压控制下的动态小信号模型,并应用PID实现其
2009-07-16 08:10:37 2754
2754 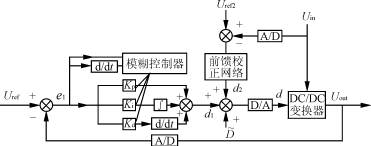
Buck-boost变换器
2009-09-23 18:32:30 1791
1791 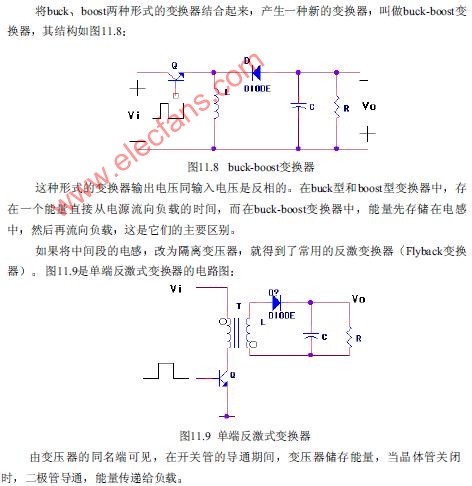
晶体管开关变换器(buck)电路
如图是晶体管开关变换器(BUCK)电路,其中晶体管Q为
2009-09-23 18:37:51 1904
1904 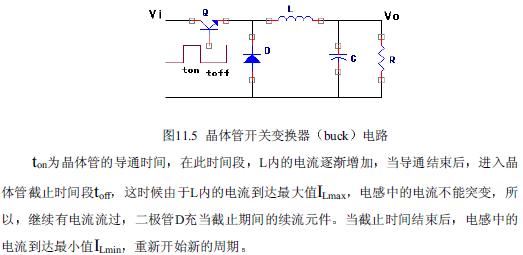
采用Buck变换器的LED驱动器反馈环路设计及测试
目前,基于降压型Buck变换器的LED驱动器广泛应用于通用的照明系统,如一些楼宇和草地的照明,通常使
2009-12-30 15:07:51 1719
1719 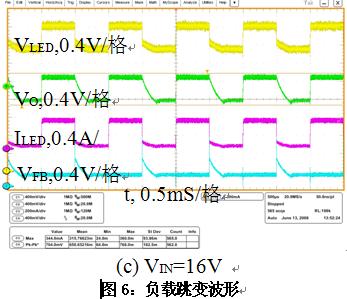
Buck变换器反馈电阻的作用
Buck变换器由于具有效率高的优点而被广泛应用于手机、GPS
2010-04-20 08:54:33 2617
2617 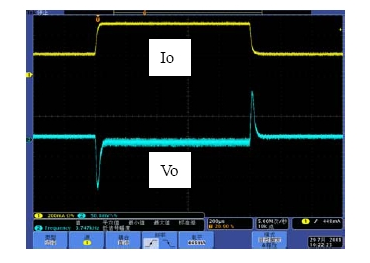
Buck 变换器只有两种工作模态,即开关管导通和开关管截止状态。首先为理想的 Buck 变换器 在一个开关周期内的两种不同工作状态建立状态方程和输出方程。这里取电感电流iL(t)和电容
2011-09-19 17:43:37 8810
8810 
为了实现对Buck变换器直流输出电压的精确控制,优化变换器的性能,提出了一种基于双滑模面控制的控制策略,建立了数学模型,并推导了变换器滑模面的存在条件。通过仿真实验表明
2013-06-25 17:07:29 72
72 Buck-Boost变换器原理升压降压原理
2016-04-28 16:59:59 158
158 本文提出一种 Bw k三电平变换器,该变换器中开关管的电压应力为输人电压的一半,采用交错控制方式,可以大大减小输出滤波器的大小。 本文详细分析 Buck 三电平变换器的工作原理,分析该变换器的输人输出特性,讨论主要参数的设计,提出一种使输人分压电容电压均衡的方法,并进行实验验证。
2016-05-10 14:24:39 7
7 Fly_buck变换器PCB布局技巧,感兴趣的小伙伴们可以瞧一瞧。
2016-11-10 11:41:20 0
0 磁集成Buck变换器在超级电容充电系统中的建模_荣德生
2017-01-04 16:57:55 3
3 基于通道控制下交错并联Buck变换器最佳换相点的研究_杨玉岗
2017-01-05 15:34:14 3
3 Buck变换器中的快标分叉控制研究_胡乃红
2017-03-19 11:26:54 0
0 Buck变换器原理详细分析
2017-09-15 17:26:25 30
30 本文主要介绍通过TL431构成的自激式Buck变换器,Buck变换器也称降压型变换器。在这个自激式DC-DC降压电路中,TL431不仅作为基准源,而且作为自激振荡的有源器件。
2017-12-13 10:51:00 11674
11674 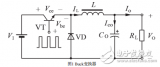
Buck 变换器的CCM等效电源平均电路模型
2017-12-19 15:25:12 9
9 本文为大家介绍buck变换器的传递函数。
2018-01-10 08:51:08 18449
18449 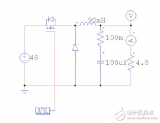
本文为大家介绍buck变换器电压模式补偿器的设计。
2018-01-10 09:39:33 4963
4963 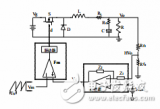
Buck变换器由功率级和反馈控制电路组成,功率级包括功率开关和输出滤波器,它将高输入电压变换到低的输出电压,反馈控制电路通过调制功率开关的占空比调节输出电压。本文对buck变换器峰值电流进行分析。
2018-01-10 09:52:29 6409
6409 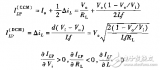
buck变换器轻载时有三种工作模式:跳脉冲模式、突发工作模式、强迫连续模式。
2018-01-10 10:15:36 16050
16050 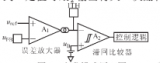
本文为大家带来buck变换器设计介绍。
2018-01-10 10:46:28 8509
8509 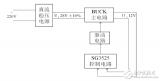
BUCK 电路是一种降压斩波器,降压变换器输出电压平均值UO 总是小于输入电压Ui。通常电感中的电流是否连续,取决于开关频率、滤波电感L 和电容C 的数值。
2018-01-10 11:16:22 14274
14274 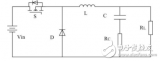
BUCK变换器在一些大功率的开关电源电路设计中,是非常常见的设计元件之一,其本身具有高转化率、高适应性等优势,能够为工程师的产品设计研发带来极大帮助。本文教大家自制buck变换器。
2018-01-10 11:37:32 4173
4173 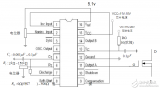
本文介绍了buck变换器工作原理_Buck变换器的降压原理分析。Buck变换器主要包括:开关元件,二极管,电感,电容和反馈环路。而一般的反馈环路由四部分组成:采样网络,误差放大器,脉宽调制器PWM
2018-01-10 17:00:33 63533
63533 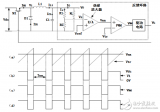
本文主要介绍了buck变换器的滤波电容电感怎么选取及用法。选择Buck变换器电感的主要依据是变换器输出电流的大小。当Buck变换器的输出电流等于maxoI时,仍然要保证电感工作在非饱和状态,这样电感值才能维持恒定不变。电感值1L的恒定确保了电感上的电流线性上升和下降。
2018-01-10 17:17:47 30220
30220 
本文介绍了非理想buck变换器模型。运用能量守恒原理将非理想型Buck变换器进行理想化转换;然后,就转换后的电路根据开关网络平均模型法建立平均变量模型,从而得到Buck变换器的大信号平均等效电路、直流等效电路和交流小信号等效电路,进而进行稳态和动态小信号特性分析。
2018-01-10 18:30:56 16471
16471 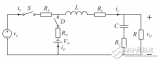
作为一种基本的DC/DC降压式变换电路, Buck变换器被广泛应用于电机的无级变速与控制。本文基于PSpice 软件,对Buck变换器进行参数仿真,对其功耗分析和吸收电路设计方面进行电路仿真。形象化
2019-08-28 17:46:27 24
24 能量双向流动,进而可以节省构建变换器的材料,并且转换效率高,因此被广泛应用于无需电气隔离的电池储能系统,光储、风储微电网系统等。 基于Buck-Boost的双向半桥DCDC变换器结构如图一所示。由图可知,这种双向DC/DC变换器本质上是Buck和Boost两种变换器构
2021-03-01 12:06:46 23496
23496 变换器是常用器件,电子相关专业的朋友对变换器通常较为了解。为进一步增进大家对变换器的认识,本文将基于两点介绍变换器:1.何为谐振变换器,2.理想/非理想buck变换器模型介绍。如果你对变换器抑或本文内容具有兴趣,不妨继续往下阅读哦。
2020-11-07 11:30:37 8543
8543 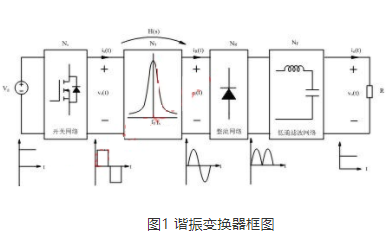
对于变换器,大家自然较为熟悉。为增进大家对变换器的认识,本文将对buck变换器进行全面讲解。本文中,你将学到buck变换器的工作原理、buck变换器的降压原理、buck变换器的工作过程以及如何进行buck变换器设计。如果你对变换器具有兴趣,不妨继续往下阅读哦。
2020-11-07 11:30:33 4842
4842 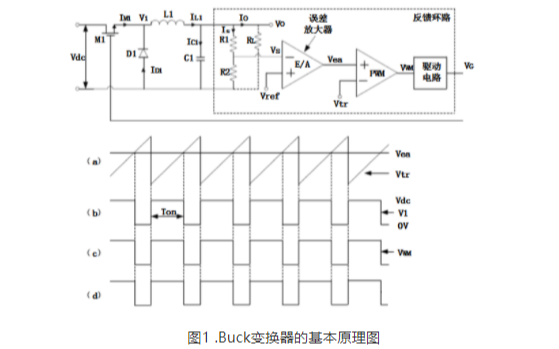
本文档的主要内容详细介绍的是Buck变换器的工作原理与设计的学习课件免费下载包括了:Buck变换器的工作原理,Buck变换器的主电路设计,Buck变换器的建模,Buck变换器的补偿网络设计
2020-12-07 08:00:00 39
39 电子发烧友网为你提供三种飞轮结构的BUCK变换器资料下载的电子资料下载,更有其他相关的电路图、源代码、课件教程、中文资料、英文资料、参考设计、用户指南、解决方案等资料,希望可以帮助到广大的电子工程师们。
2021-03-31 08:42:47 0
0 本文介绍了在通信系统中,同步Buck变换器上部功率MOSFET和下部功率MOSFET的工作特点,同时讨论了在设计高效率的同步Buck变换器时,选取上部和下部功率MOSFET原则;介绍了一种新型的采用
2021-05-05 16:57:00 4197
4197 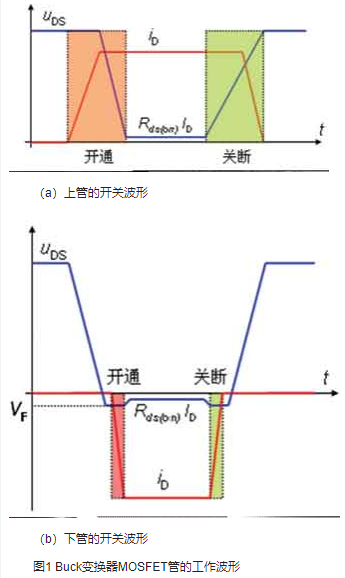
Buck变换器的DCM稳态关系说明。
2021-06-10 16:29:30 17
17 Buck变换器中的直流滤波电感设计公式分享下载。
2021-06-19 14:57:24 27
27 上一节提到的开关电源的系统框图中,DC-DC变换器是其中一个重要的组成部分DC-DC变换器最基础的主要有三种:Buck变换器,Boost变换器和Buck-Boost变换器Buck变换器:即降压变换器
2021-10-22 10:36:03 9
9 1.前言在DCDC变换器中BUCK变换器是最基础的一类降压型变换器,它可以将输入电压降低后输出。在连续模式CCM下,输出和输入之间的比值是D(D为占空比)。这种开关变换器是一种通过电子开关周期分合
2021-10-22 18:51:08 10
10 1 Buck 变换器的功率器件设计公式 (1):Buck 变换器的电路图: (2):Buck 变换器的主要稳态规格: (3):功率器件的稳态应力: -- 有源开关 S: -- 无源开关 D: 上述
2023-06-26 10:06:01 434
434 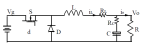
Buck变换器的工作原理基于一个简单的电路,由一个电感和一个开关组成,开关被称为MOSFET。在Buck变换器电路中,开关周期性地将电流流入电感,并将电流从电感流入输出电容。在输入和输出之间的电感上产生的电压与输出电压相加,这种方法可以有效地降低输出电压并控制其波动。
2023-08-26 09:58:11 1133
1133 首先放一张BUCK变换器的基本电路图。
2023-09-21 16:39:38 3571
3571 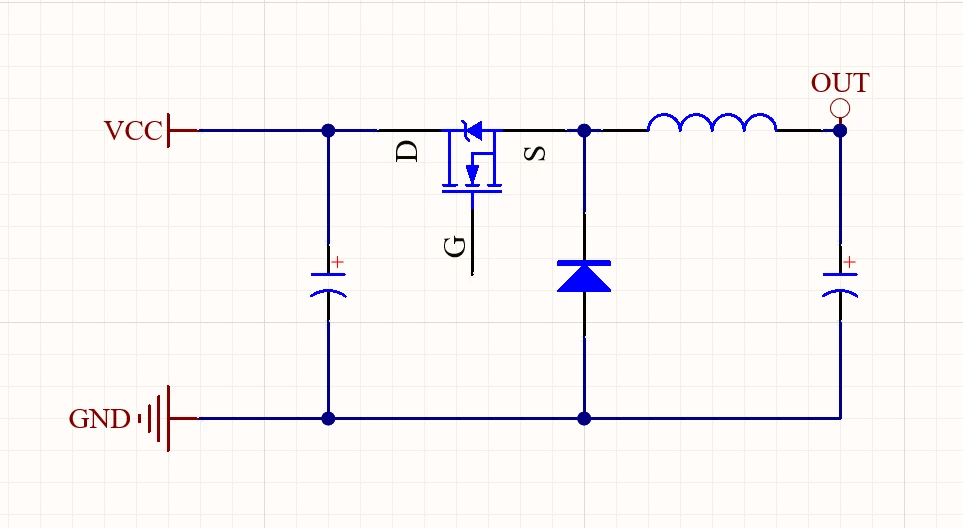
基于Buck变换器Matlab闭环仿真
2023-09-28 16:44:34 1108
1108 
电子发烧友网站提供《电压反馈型BUCK变换器的环路补偿设计.pdf》资料免费下载
2023-11-01 09:18:56 2
2
 电子发烧友App
电子发烧友App




















































评论