傅立叶级数函数用于查找电路的稳态响应。有四种不同类型的对称性可用于简化评估傅里叶系数的过程。
对称性的影响
偶函数对称性
奇函数对称性
半波对称
四分之一波对称
偶函数对称
当且仅当
f ( t )= f ( - t )1.1
如果函数满足Eq。 1.1,然后它被认为是因为只有偶数指数的多项式函数具有这种类型的行为。对于任何偶数周期函数,傅里叶系数的方程式简化如下:
$$ a_ {v} = \ frac {2} {T} \ int_ {0 } ^ {T/2} f(t)dt。$$(1.2)
$$ a_ {k} = \ frac {4} {T} \ int_ {0} ^ {T/2所有 k (1.4)的f(t)\ cos k \ omega _ {0} tdt。$$(1.3)
$$ b_ {k} = 0 $$ )
注意方程式1.4,如果函数是偶数,则所有 b 系数都为零。下面,图1.1描绘了偶数周期函数。以下两个衍生物完全遵循方程式。 1.2 - 1.4。通过每次推导,选择$$ t_ {0} = -T/2 $$,然后我们将积分间隔从 - T /2分解为0和0到 T /2,或如下
$$ a_ {v} = \ frac {1} {T} \ int _ { - T/2} ^ { T/2} f(t)dt $$
$$ = \ frac {1} {T} \ int _ { - T/2} ^ {0} f(t)dt + \ int_ { 0} ^ {T/2} f(t)dt。$$(1.5)
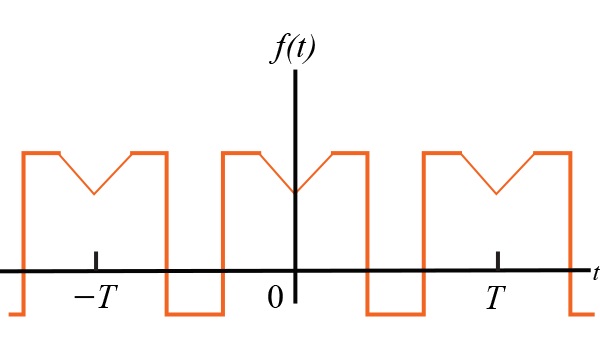
图1.1偶数函数off(t)= f(-t)
现在,必须更改积分变量在方程式右边的第一个积分中。 1.5。特别是,我们可以让 t = - x 并观察 f ( t )= f ( - x )= f ( x ),因为函数是偶数。当 t = - T /2和 dt x = T /2 = -dx 。因此
$$ \ int _ { - T/2} ^ {0} f(t)dt = \ int_ {T/2} ^ {0} f(x) (-dx)= \ int_ {0} ^ {T/2} f(x)dx。$$(1.6)
它确实表明从 - T /2到0与从0到 T /2的积分相同。因此,Eq。 1.5与Eq相同。 1.2。得出方程1.3可以完成如下:
$$ a_ {k} = \ frac {2} {T} \ int _ { - T/2} ^ {0} f( t)\ cos k \ omega _ {0} tdt + \ frac {2} {T} \ int_ {0} ^ {T/2} \ cos k \ omega _ {0} tdt $$(1.7)
但是
$$ \ int _ { - T/2} ^ {0} f(t)\ cos k \ omega _ {0} tdt = \ int_ {T/2} ^ { 0} f(x)\ cos(-k \ omega _ {0} x)( - dx)$$
$$ = - \ int_ {0} ^ {T/2} f(x )\ cos k \ omega _ {0} xdx。$$(1.8)
同样,如前所述,从 - T /2集成到0与从0到 T /2的积分相同。通过结合Eq。 1.7与Eq。 1.8,Eq。 1.3是生产的。在此之后,当 f ( t )是偶数周期函数时,所有 b 系数都为零,因为积分来自 - T /2到0是从0到 T /2的积分的精确负数。因此,
$$ \ int _ { - T/2} ^ {0} f(t)\ sin k \ omega _ {0} tdt = \ int_ {T/2} ^ {0} f(x)\ sin( -k \ omega _ {0} x)( - dx)$$
$$ = - \ int_ {0} ^ {T/2} f(x)\ sin k \ omega _ {0 } xdx。$$(1.9)
现在,如果Eqs。 1.2和1.3用于查找傅里叶系数,积分区间必须介于0和 T /2之间。
奇函数对称
如果
f ( t )= - f ( t )(1.10)
满足公式的函数。 1.10被认为是奇数,因为只有奇数指数的多项式函数就是这样的。傅里叶系数的表达式如下:
$$ a_ {v} = 0; $$(1.11)
$$ a_ {k} = 0,所有的$$ K表; (1.12)
$$ b_ {k} = \ frac {4} {T} \ int_ {0} ^ {T/2} f(t)\ sin k \ omega _ {0} dt 。$$(1.13)
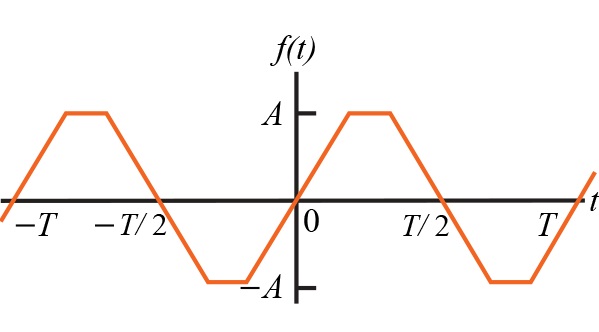
图1.2
看着Eqs。 1.11 - 1.13,如果周期函数为奇数,则所有 a 系数均为零。上图显示了奇数周期函数。在方程式上使用相同的推导方法。 1.11 - 1.13,用于推导方程式。 1.2 - 1.4。
通过沿时间轴移动周期函数,可以拆除函数的均匀度(奇数)。从本质上讲,这意味着明智地选择 t = 0的位置可能会产生奇数或偶数对称的函数。例如,图1.3(a)中的三角函数不是偶数或奇数。然而,如图1.3(b)所示,该函数可以是偶数,或者是奇数,如图1.3(c)所示。
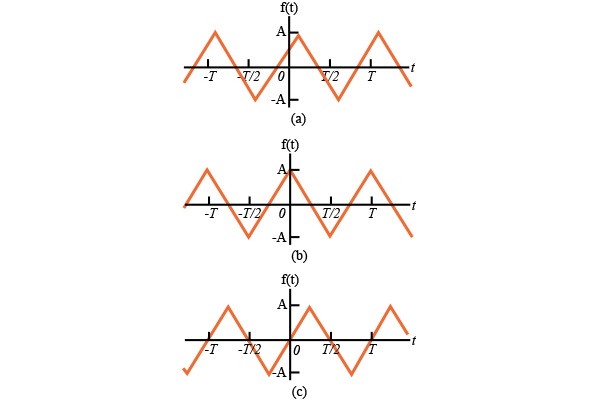
图1.3
半波对称
如果满足以下约束,则称该函数具有半波对称性:
f ( t )= - f ( t - T /2)(1.14)
公式1.14表示一个周期函数具有半波对称性,如果它在被移动了一半的周期后被反转,那就说与原始周期函数相同。例如,图1.2和1.3中所示的周期函数具有半波对称性,而图1.4和1.5中的那些函数不具有这种对称性。对于 t = 0,半波对称性不作为函数存在。
如果给定函数确实具有半波对称性,则 a
k 的偶数值,em> k 和 b k 被定义为零。类似地,由于具有这种对称性的周期函数的平均值零, a v 也为零。傅里叶系数的表达式如下:
$$ a_ {v} = 0,$$(1.15)
$$ a_ {k} = 0,$$ k 偶数(1.16)
$$ a_ {k} = \ frac {4} {T} \ int_ {0} ^ {T/2 } f(t)\ cos k \ omega_ {0} tdt,$$ k odd(1.17)
$$ b_ {k} = 0,$$ for k even(1.18)
$$ b_ {k} = \ frac {4} {T} \ int_ {0} ^ {T/2} f(t)\ sin k \ omega_ {0} tdt,$$ k odd(1.19)
这些方程式来源于上一篇文章中的方程1.2 - 1.4,了解傅立叶系数。选择从 - T /2到 T /2的积分间隔,然后将此范围划分为间隔 - T /2到0和0到 T /2。
$$ a_ {k} = \ frac {2} {T} \ int_ {t_ {0 }} {t_ {0} + T} f(t)\ cos k \ omega_ {0} tdt $$
$$ = \ frac {2} {T} \ int _ { - T/2} ^ {T/2} f(t)\ cos k \ omega_ {0} tdt $$
$$ = \ frac {2} {T} \ int _ { - T/2} ^ {0} f(t)\ cos k \ omega_ {0} tdt $$
$$ + \ frac {2} {T} \ int_ {0} ^ {T/2} f(t )\ cos k \ omega_ {0} tdt $$(1.20)
从此处,右侧第一个积分中的变量发生变化。
吨 = X - Ť/2
然后
x = T /2,如果 t = 0
x = 0,如果 t = - T /2;
dt = dx
重写第一个积分,
$$ \ int _ { - T/2} ^ {0} f(t)\ cos k \ omega_ {0} tdt = \ int_ {0} ^ {T/2} f(x - T/2)\ cos k \ omega_ {0}(x - T/2)dx $$(1.21)
考虑到
$$ \ cos k \ omega_ {0}(x - T/2)= \ cos(k \ omega_ {0} x - k \ pi)= \ cos k \ pi \ cos k \ omega_ {0} x $$
和b假设,
f ( x - T /2)= - f ( Ix )
因此,Eq。 1.21现在可以写成
$$ \ int _ { - T/2} ^ {0} f(t)\ cos k \ omega_ {0} tdt = \ int_ {0} ^ {T/2} [ - f(x)] \ cos k \ omega_ {0} tdt $$(1.22)
通过包括Eq。 1.22进入方程1.20,
$$ a_ {k} = \ frac {2} {T}(1 - \ cos k \ pi)\ int_ {0} ^ {T/2} f(t )\ cos k \ omega_ {0} tdt $$(1.23)
但是,如果 k 为偶数,则$$ \ cos k \ pi $$等于1,如果 k 为奇数,则为-1。
总而言之,具有半波对称零平均值的周期函数的傅里叶级数的表示仅包含奇数谐波。
四分之一波对称
如果一个函数具有关于正和负半周期中点的半波对称性和对称性,则称周期函数具有四分之一 - 波对称。该功能如图1.4所示;据说图1.4(a)中的函数关于正半周期和负半周期的中点具有四分之一波对称性。图1.4(b)中的函数没有这种对称性,但它确实具有半波对称性。
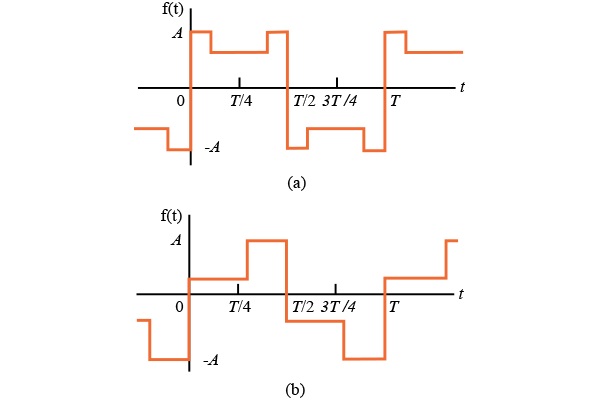
图1.4
通过选择 t = 0的位置,具有四分之一波对称性的函数总是可以是偶数或奇数。例如,图1.4(a)中的周期函数是奇数,可以通过沿着 t 向左或向右移动 T /4个单位变成偶数函数 - 轴。但是,因为图1.4(b)中的周期函数只具有半波对称性,所以它不能是偶数或奇数。
如果要使周期函数均匀,那么
$$ a_ {v} = 0,$$由于半波对称
$$ a_ {k} = 0,$$ for k 偶数,由于半波对称性
$$ a_ {k} = \ frac {8} {T} \ int_ {0} ^ {T/4} f(t) \ cos k \ omega_ {0} tdt,$$ k 奇数
$$ b_ {k} = 0,所有 k 的$$ ,因为周期函数是偶数(1.24)
上面的Eqs。 1.24是周期函数对称性的结果,除了它是偶数。如果四分之一波对称性叠加在半波对称上, a v 和 a k 因此, k 甚至可以被淘汰。看一下 a k 和 k odd,Eq的表达式。 1.19表明,当四分之一波对称性与均匀度相结合时,积分范围从0到 T /2缩短为0到 T /4。
如果四分之一波对称周期函数为奇数,
$$ a_ {v} = 0,$$由于函数为奇数
$$ a_ {k} = 0,所有 k 的$$,由于函数为奇数
$$ b_ {k} = 0,$$ for k 甚至,由于半对称性
$$ b_ {k} = \ frac {8} {T} \ int_ {0} ^ {T/4} f( t)\ sin k \ omega_ {0} tdt,$$ k 奇数(1.25)
上面的1.25的Eq因此而来四分之一波对称性和奇数。与均匀度相似,四分之一波对称性允许从0到 T /2到0到 T /4的积分间隔缩短。
即将到来
截至目前,您应该更好地了解傅立叶系数和可能发生的不同类型的对称性。这五种类型,偶数,奇数,半波,四分之一波半波甚至四分之一波半波都用于简化傅立叶系数的计算。下面将介绍的一些主题将深入探讨傅立叶级数的线性电路的稳态响应,周期函数的平均功率计算,以及此类周期函数的均方根值。
-
傅立叶
+关注
关注
0文章
36浏览量
12425 -
傅立叶变换
+关注
关注
3文章
98浏览量
32103
发布评论请先 登录
相关推荐
什么是电源滤波器 常用电源滤波器电路形式
对称电池测试怎么分析?什么是软短路,什么是硬短路?
对称短路有哪些 对称短路的形式有哪四种
ADC噪声系数的重要性
adi_sport_ConfigClock的时钟分频系数和pcg clk的分频系数有什么关联?
差动放大器中两管及元件对称对电路性能有何影响?
如何用分子钟跃迁探测对称性破缺
如何证明波导正规模的电场磁场具有时间对称性和反对称性?
傅立叶变换成f和w关系
傅立叶余弦逆变换公式总结
傅立叶变换的频移特性的应用
傅立叶变换的条件的理解
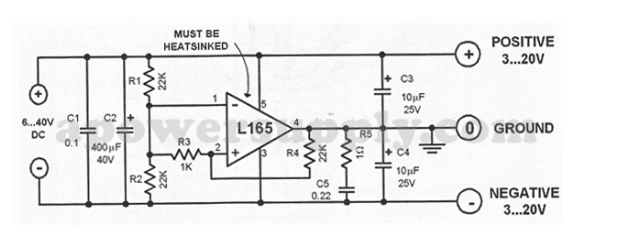
基于L165的对称电源原理图解





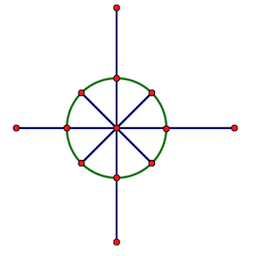
 对称性对傅立叶系数的影响有哪些
对称性对傅立叶系数的影响有哪些










评论