10.3.1 幂级数及其收敛性
定义：形如
（a为实数）的级数称为幂级数。
收敛半径：任意幂级数
必存在数r>=0使得
(i) 这一幂级数在(-r,r)内必区间一致收敛且绝对收敛
(ii)若幂级数在x=r收敛，则对任意
，这一幂级数在[-r,r]一致收敛，若幂级数在x=r收敛，亦有相同的结果。
(iii)对任意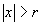
，幂级数在x发散。
则称r为幂级数的收敛半径。
显然，只须求出r，则幂级数的收敛性就可以知道。
r的求法：若
，或
存在
，则幂级数的收敛半径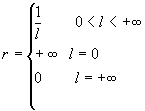
10.3.2 泰勒级数的定义
若函数f（x）在点
的某一临域内具有直到（n+1）阶导数，则在该邻域内f（x）的n阶泰勒公式为：
其中：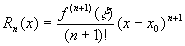
，称为拉格朗日余项。
以上函数展开式称为泰勒级数。
10.3.3 泰勒级数在幂级数展开中的作用：
在泰勒公式中，取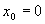
，得：
这个级数称为麦克劳林级数。函数f（x）的麦克劳林级数是x的幂级数，那么这种展开是唯一的，且必然与f（x）的麦克劳林级数一致。
注意：如果f（x）的麦克劳林级数在点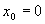的某一临域内收敛，它不一定收敛于f（x）。因此，如果f（x）在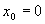处有各阶导数，则f（x）的麦克劳林级数虽然能做出来，但这个级数能否在某个区域内收敛，以及是否收敛于f（x）都需要进一步验证。