在国际标准“ISO11452-2”的抗扰度测试中,本产品作为传感器输出信号等的阈值判断用比较器,在各种噪声频段均表现出极其出色的抗干扰性能,输出电压波动均在±1%以内。
2019-10-17 16:17:30 1136
1136 
中值滤波可以很好地过滤掉各种噪音数据,另外,还可以很好地保留边缘信息。此程序可以对一维二维三维信号,进行中值滤波,完成噪声的去除。Median filtering Median filtering
2011-08-16 13:50:27
,
NF_STRENGTH_HIGH,
NF_STRENGTH_MAXNUM
] UI_NF_STRENGTH;
如果一直是开到最大nf去噪,是否有坏的效果,影响图像质量
2018-06-21 12:36:08
的方法进行目标图像的分割。矩不变阈值分割法就是把矩法用于图像的分割,其基本思想是:使阈值分割前后,图像的矩保持不变[3]。矩不变阈值法可以看作是一种图像变换,它将原始模糊图像变换成理想图像。二维图像的第k
2018-08-24 16:22:26
AD9914 DRG非驻留模式配置扫频连续波,SPAN打窄,噪底固定时间跳动,观察DROVER信号时序发现drover的上升沿时间不同且drover高电平持续时间会变,有大佬知道这是什么原因
2024-01-22 00:48:16
这个小波去噪程序,我不知道为什么有以下错误?求各位大神帮我看看
2018-01-26 19:31:09
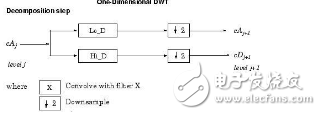
1899.1.1 小波通用函数1929.1.2 小波函数1989.1.3 一维连续小波变换的函数简介2029.1.4 一维离散小波变换的函数简介2039.1.5 一维平稳小波变换的函数简介
2015-11-01 10:35:50
现在我手上一段含噪的音频文件(.wav格式),要求通过dsp对音频信号进行去噪但是不知道怎么写c代码将.wav文件读进去进行后续处理,求大神指导一下啊
2014-12-19 21:42:54
在labview中运用matlab脚本对声信号进行小波去噪,想知道,matlab脚本的输入输出数据类型是不是设置为一维数组,在matlab中矩阵可以显示出波形,在labview中是不是不行?还是要转换为波形文件?怎么转换呢?求帮助!!!
2012-05-04 16:47:21
最近用labview做小波去噪,去的是调用matlab script节点的方法,用wden函数实现小波去噪,比如xd1=wden(x,'heursure','s','sln',lev,'sym8
2014-03-05 15:14:36
(我的目的时求两个波头之间的距离,现在已经知道怎么求峰值了,但是一个波头上有多个峰值,所以需要筛选)labview中,一维数组中相邻元素进行比较,差值和某一阈值近似相等,输出该差值,还有当有多个差值
2019-01-14 20:27:17
刚接触labview,在做基于labview的数字音频处理器的毕设时碰到的问题,查找了很多相关文献之后,参考这些文献我写出下面这些程序,文献里都是直接创建一个带有噪声的波形来进行去噪然后显示去噪后
2017-04-08 10:04:14
建模,数学建模需求1:matlab非线性鲁棒仿真需求2:滚动轴承动力学建模需求3:维纳滤波去噪,小波阈值去噪,ICA去噪需求4:matlab的车牌识别需求5:储能电池参与电网一次调频等效模型需求6
2021-06-02 16:00:47
无线电通信中的电磁波干扰,看不见,摸不到,也无法呈现,有时会碰到这样的问题:同一组设备、在相同的环境中,有的时间段无线通信很好,有的时间段突然无线通信的信号质量严重下降,这个是怎么回事? 由于目前
2022-02-25 12:15:45
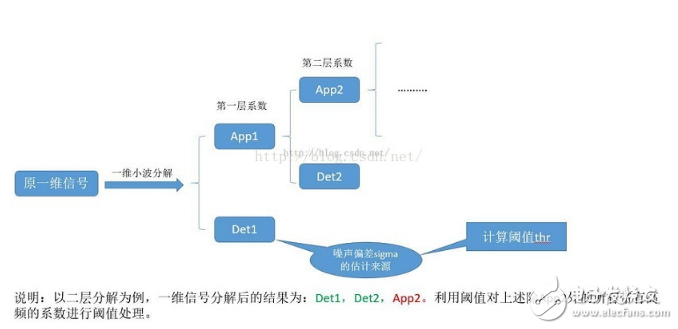
是一种实现简单、结果较好的小波降噪方法。阈值去噪方法就是对小波分解后的各层系数中模大于和小于某阈值的系数分别处理,然后对处理完的小波系数进行反变换,重构经去噪的信号。在现实情况下,有用的信号通常是低频信号
2019-08-06 04:00:00
为什么用小波去噪一个程序得出的信噪比不一样呢?
2023-04-25 11:15:18
阈值比默认阈值更具有可信度。 (3)一维小波的重构。根据小波分解的第N层的低频系数和经过量化处理后的第1层到第N层的高频系数,进行一维信号的小波重构。4 网络化虚拟小波消噪仪的设计4.1小波消噪仪
2019-04-19 09:40:07
,需要用到信号去噪的知识,发现有个专用的小波去噪算法,但是根本看不懂。问题:1.只是想把“小波去噪”这种知识拿来当工具用,但我几乎没这方面的基础,我现在应该把数字信号处理知识捡起来从头学起吗? 2.我
2014-07-28 15:08:54
图像多小波阈值去噪方法具体有哪些?哪位能给点相关资料啊,感激不尽、
2015-05-14 22:39:36
采集到的数据是1维列数组,是实时采集,比如1秒一次数据,一种简单去噪的方法就是叠加平均,问题是怎么把每10秒的数据叠加平均啊? 索引那块用的不大好。。真心求帮助。。。谢
2012-05-12 08:53:04
方法是一种实现简单、结果较好的小波降噪方法。阈值去噪方法就是对小波分解后的各层系数中模大于和小于某阈值的系数分别处理,然后对处理完的小波系数进行反变换,重构经去噪的信号。在现实情况下,有用的信号通常是
2015-01-16 15:21:49
研究生导师给出了一个题目基于因子分析设计心电信号去噪算法,可是在大学课程中没有做过相关的设计,自己想了很久,一点思路也没有,希望能得到大家的帮助,有哪位做过相关设计,或者分享一下相关设计的链接,给出
2020-08-05 07:00:28
之后加入小波阈值去噪过程,再通过变换域低通滤波插值估计进行双重去噪处理。计算机仿真结果表明,该估计方法能够有效地去除加性高斯白噪声,比一般的LS估计算法性能要好,在一定程度上弥补了LS估计算法对噪声
2010-05-06 09:01:31
我想用matlab模拟一个简单的含噪的地震信号 然后用小波分析去噪 但是自己纯小白一个不知道怎么下手 求大佬指导
2020-12-09 18:00:31
提升小波变换由哪几个步骤构成?如何在TMS320VC5509A型DSP的硬件平台上实现毫米波探测器回波信号的实时去噪处理?
2021-04-20 06:04:22
如何实现极低信噪比条件下的小波变换去噪法?小波变换检测微弱信号的工作原理是什么?
2021-04-07 06:00:54
例如一个周期的正弦波和高斯白噪声混合后,经过1000次叠加消噪,还原查正弦波呢? 谢谢各位大神了
2013-09-09 13:50:25
三角波信号发生器的原理是什么?三角波信号发生器的设计约束是什么?如何采用CMOS工艺去设计三角波信号发生器?
2021-04-13 06:26:12
对采集的信号进行去噪,我们选择巴特沃斯带通滤波器,,怎么样巴特沃斯的阶数,怎么算呀,求帮助
2017-03-02 16:42:03
检测四个冲击的位置,但是第三个和第四个噪声干扰很大,波峰检测不准确,如何利用小波去噪去除图中噪声的干扰。
2016-05-12 12:09:25
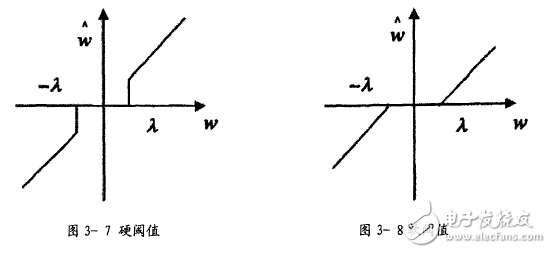
小波阈值去噪的基本原理小波阈值去噪的基本思想是先设置一个临界阈值λ,若小波系数小于λ,认为该系数主要由噪声引起,去除这部分系数;若小波系数大于λ,则认为此系数主要是由信号引起,保留这部分系数,然后
2020-11-06 06:31:58
小波理论分析与信号处理本篇对小波分析的基本理论作了全面的介绍。将一维小波理论和高维小波理论放在一起并行介绍,强调小波基的选择、小波框架的建立是本篇的一大特点。读者从本篇中可以发现小波分析引人入胜
2009-11-25 14:45:31
层到第N层的各层高频系数,将二维信号进行小波重构。在以上的三个步骤中,选取阈值以及阈值量化处理是重点,以下进行实例操作,其中用到的ddencmp和wdencmp是MATLAB的去噪函数,具体如下
2021-03-29 09:48:24
('振幅/m');%用db4小波对原始信号进行8层分解并提取系数[C,L]=wavedec(d,8,'db8');%用ddencmp()函数获得信号的默认阈值,使用wdencmp()命令函数实现去噪过程
2013-05-11 08:12:34
现在有小波去噪够的局部放电数据,怎么绘制q-n图谱或者是三维的图谱,prpd图。
2023-04-26 17:54:28
怎样去编写一种基于DSP的正弦波信号发生器源程序呢?
2021-11-19 06:29:49
怎样去设计9/7二维离散小波变换系统?如何对9/7二维离散小波变换系统进行仿真?
2021-05-07 07:09:09
时域采样的相关知识;(4)掌握信号频谱的概念;(5)掌握滤波器的设计方法;(6)通过对语音去噪的处理,更深刻地理解了信号频谱的含义,也加深了对滤波器作用的理解。2.实习要求录制一段自己的语音信号,要求
2011-09-29 22:42:49
数字IC电源静噪与去耦应用手册
2012-08-18 11:18:19
数字IC电源静噪和去耦应用手册
2012-08-20 14:23:53
如题,正在做电能质量分析的毕设,仿真三相电压/电流(已加入噪声),我现在想设计一个去噪模块,不知道用什么方法(小波?)。另外,有没可能将暂态和稳态分离开来
2014-04-11 21:58:32
办法: 在“WiMi-net无线自组网管理平台”软件的“信道部署”页面点击“自动搜索”就可以搜索电磁波噪声,观察本底噪声(包括平均底噪和极大底噪)。一般在无干扰环境中,平均底噪数值在-105dBm附近,极大
2022-11-23 10:24:34
请问怎么把小波去噪和均值或中值结合啊?方便给个简单的编码吗?,谢谢
2019-03-25 20:22:30
cdl=detcoef(c,l,1);%提取第一层的高频系数%下面利用默认阈值进行消噪处理%用ddencmp函数获得信号的默认阈值,使用wdencmp命令函数来实现消噪过程[thr,sorh
2011-05-26 22:19:21
最近刚学labview,想问下方波叠加一个正弦波和均匀白噪声该怎么利用labview除噪得到方波呢?求思路点拨,拜托拜托
2016-11-11 19:35:37
这是一个小波去噪程序,其他部分我都看懂了就是这个循环里,那几个写着visible的控件不知道是啥,求大神帮忙,非常感谢
2016-07-17 09:17:02
求用vrilog语言的用双边滤波算法的图像去噪程序代码。谢谢,急!!!
2013-05-12 21:36:28
求一个labview和matlab小波去噪的教程,信号源是个txt文件
2017-06-01 22:43:34
新手到来,请多多关照,诸位谁有关于小波去噪和LMS自适应滤波器算法的,可以共享一下不?谢谢啦~~
2016-04-19 21:02:16
(I,[2 4]);%采用二维中值滤波函数medfilt2对受椒盐噪声干扰的图像滤波figureimshow(I)title('去噪之后的图像')%图像锐化[M,N]=size(I);% 计算图像的尺寸
2020-04-01 19:03:19
,证明CTL信号有控制作用。是什么原因引起该噪波带呢?由录像机工作原理分析,在放像状态,主导伺服的控制路径有两条,一条是控制磁迹信号(CTL信号),另一条是速度控制信号(主导FG信号),两路信号叠加后共同
2009-10-21 09:43:11
如图所示,matlab读取212类型数据库代码是在网上找的,可以读取,但是我要用这个信号做小波去噪,要用小波工具箱,所以怎么把这个读取出来的数据变成.mat格式
2020-11-04 22:06:26
本帖最后由 一只耳朵怪 于 2018-5-24 08:37 编辑
输入一组信号,这组信号来源于一台6缸天然气发动机,记录的是机体振动信号。经过 一维离散小波变换 分析后结过如图所示:我现在不太懂这两幅图分别显示的什么信息,请大神指教!
2018-05-23 23:03:18
请问各位兄弟姐妹,谁有一维波形去噪程序啊
2011-08-16 13:33:42
音频信号的细化普设计及去噪
2012-08-20 16:05:09
本文采用小波阈值去噪方法,利用了小波变换多分辨率的特点,它对信号具有自适应性,可以降低消噪算法的复杂程度,又可保证心电信息特征不被丢失。试验表明,该方法能较
2009-11-27 11:40:45 21
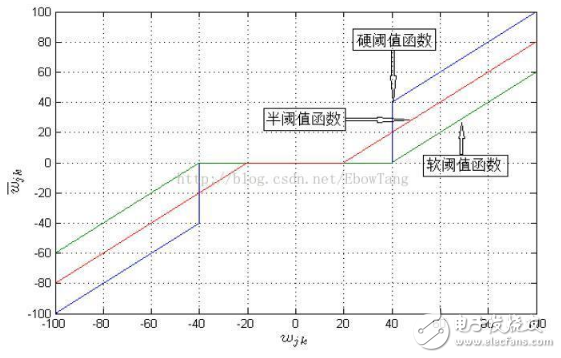
21 针对传统软硬阈值方法存在的估计小波系数连续性差和信号失真等问题,采用了三种改进的小波阈值消噪方法,通过对仿真含噪信号进行消噪分析及计算信噪比、赋范均方根误差
2009-12-30 16:48:43 10
10 该文针对传感器网络中无线链路的不稳定性问题,基于r 邻居图模型提出一种具有稳定链路的鲁棒可调拓扑控制算法RAWSL (Robust Adjustable with Steady Links)。算法以接收信号强度阈值作为
2010-02-10 15:03:03 10
10 摘要:本文通过对施密物电路的跳阈分析,指出在二值TTL施密物电路中实现该一功能的核心部件为阈值可控的差动电流开关。根据三值TTL电路有两个信号检测阈值的特点,本文设计
2010-05-11 10:19:23 18
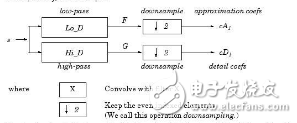
18 小波阈值去噪原理 2.1 小波变换 傅立叶分析是将信号分解成一系列不同频率的正弦波的叠加,同样小波分析是将信号分解成一系列小波函数的叠加,而这些小波函数都是一个母小波函数
2011-03-25 16:41:50 172
172 小波模极大值改进去噪算法把阈值去噪和Witkin的尺度跟踪理论结合,剔除由噪声产生的模极大值点,可有效恢复信号。与传统的阈值去噪法和基于平移不变量的去噪算法相比,该算法提
2011-05-31 15:07:20 35
35 磁阻传感器 将车辆引起的地磁扰动转换为清晰的电压信号,采用阈值算法可得到交通流量、车长、车速等多种信息。地磁检测器是环形线圈的理想代替技术,国内外许多学者对基于地磁
2011-07-26 15:47:53 68
68 本文主要介绍了小波去噪阈值如何选取_小波阈值分析。小波去噪过程就是利用小波分解将图像信号分解到各尺度中,然后把每一尺度中属于噪声的小波系数去掉,保留并增强属于信号的小波系数,最后利用小波逆变换将处理
2018-01-10 09:08:47 57528
57528 
本文主要介绍了一种基于新阈值函数的小波阈值去噪算法。在小波阈值去噪法中的两个重要的因素—阈值选取方式和阈值函数,直接决定图像去噪的效果,所以要针对噪声和图像选取合适的阈值函数和最佳阈值,才能最大程度去除图像噪声。本文提出了新的阈值函数,这一函数既满足函数的连续性,又解决了阈值函数恒定偏差问题。
2018-01-10 10:12:56 9059
9059 
介绍了小波阈值去噪的三种应用:小波阈值去噪技术在ECG信号处理中的应用、小波阈值去噪技术在电能质量检测中的应用和小波阈值技术在生物医学信号处理中的应用。利用小波阈值去噪是新发展起来的去除噪声的方法,利用小波阈值去噪具有良好的效果,可以有效提高信噪比。
2018-01-10 14:25:08 5533
5533 
本文主要介绍了小波软阈值的推导_软阈值的计算。由于噪声信号强度的随机性,以及小波分解过程中信号与噪声的传播特性不同,每一层小波分解系数所采用的阈值应该是随小波系数的变化而变化的。能实现这种变动阈值的方法就是软阈值去噪方法。小波软阈值的具体计算原理和计算步骤如下。
2018-01-10 14:46:19 4809
4809 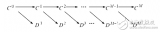
突破传统 采集+无线数传一体 众山科技-智能采集终端|RTU(型号:ZSR2184)提供8路模拟量(0~20mA)信号采集、4路开关量信号采集,可以接续各种现场传感器的模拟信号及开关量信号,支持阈值
2018-07-17 11:47:42 6433
6433 接下来是测量得到的同步功率和同步信号的 CINR。在移动网络中,基于 CINR,设备将确定检测到的小区是否是要驻留的小区。这通常根据定义为最小 CINR(该最小 CINR 基于同步信号确定)的阈值来确定。对于 LTE 来说,这是-6dB,对于此“Pre-5G ”,有待正在进行的现场试验做出评估。
2019-10-14 08:44:02 7772
7772 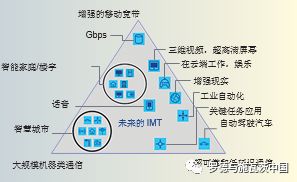
,可在输出电压实现稳压后通知系统。要实现必要的操作,您可以调整 PG 阈值电压和延迟。PG 信号的阈值电压通
2019-12-27 08:00:00 9
9 基于荧光方法的诊断检测需要借助一个阈值去检测荧光。如果接收的荧光信号低于阈值水平,则无法确定样本中存在目标分析物。系统中的电子器件和一些其他因素可能产生背景噪声使得阈值增高。为降低阈值水平,同时持续稳定地获得更出色的灵敏度而不牺牲选择性,我们需要谨慎设计光学检测系统,确保信号链不会提高背景噪声的水平。
2023-06-12 16:18:04 284
284 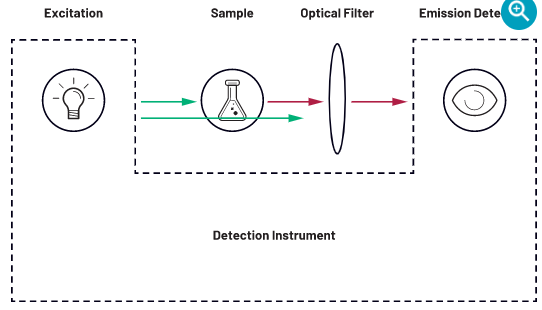
噪声类型(杂波)和信号(目标);比较信号分离(阈值检测);信号统计.参数估计
基于所需P值的阈值确定;恒虚警探测器设计;检测性能
2023-07-15 12:54:32 390
390 
比较器常用于电压比较、信号判断和触发器等应用中。它可以用于检测信号的高低、阈值判断、数字信号的转换等。比较器具有高速和高精度的特点,可以快速响应输入信号的变化,并输出相应的结果。
2024-02-09 06:52:00 2001
2001 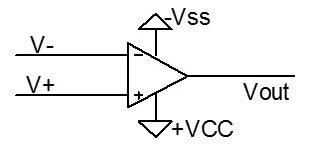
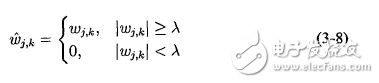
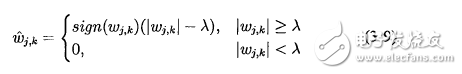
 电子发烧友App
电子发烧友App





























评论